Les méthodes nouvelles de la mécanique céleste/Chap.27

Henri Poincaré

Les méthodes nouvelles de la mécanique céleste

Gauthier-Villars, 1899 (3, p. 175-200).

CHAPITRE XXVII.

THÉORIE DES CONSÉQUENTS.

---

305.Nous pouvons encore tirer de la théorie des invariants intégraux d’autres conclusions qui nous seront utiles dans la suite, en la présentant sous une forme un peu différente.

Commençons par examiner un exemple simple. Soit un point dont les coordonnées dans l’espace soient $x,$ $y$ et $z$ et dont le mouvement soit défini par les équations

(1)

${\begin{aligned}{\frac {dx}{dt}}&=\mathrm {X} ,&{\frac {dy}{dt}}&=\mathrm {Y} ,&{\frac {dz}{dt}}&=\mathrm {Z} .\end{aligned}}$

$\mathrm {X} ,$ $\mathrm {Y}$ et $\mathrm {Z}$ sont des fonctions données et uniformes de $x,\,y,\,z\,;$ supposons d’abord que $\mathrm {X}$ et $\mathrm {Y}$ s’annulent tout le long de l’axe des $z,$ de telle façon que

$x=y=0$

soit une solution des équations (1).

Posons ensuite

${\begin{aligned}x&=\rho \cos \omega ,&y&=\rho \sin \omega ,\end{aligned}}$

les équations (1) deviendront

(2)

${\begin{aligned}{\frac {d\rho }{dt}}&=\mathrm {R} ,&{\frac {d\omega }{dt}}&=\Omega ,&{\frac {dz}{dt}}&=\mathrm {Z} ,\end{aligned}}$

où $\mathrm {R} ,$ $\Omega$ et $\mathrm {Z}$ sont des fonctions de $\rho ,$ $\omega$ et $z,$ périodiques de période $2\pi$ par rapport à $\omega .$

Nous conviendrons de ne donner à $\rho$ que des valeurs positives, et nous pourrons le faire sans difficulté puisque $x=y=0$ est une solution.

Je suppose maintenant de plus que $\Omega$ ne puisse jamais s’annuler et, par exemple, reste toujours positif ; alors $\omega$ sera toujours croissant avec $t.$

Imaginons qu’on ait intégré les équations (2) et qu’on en présente la solution sous la forme suivante

${\begin{aligned}\rho &=f_{1}(\omega ,a,b),&z&=f_{2}(\omega ,a,b).\end{aligned}}$

Les lettres $a$ et $b$ représentent des constantes d’intégration.

Soit

${\begin{aligned}\rho _{0}&=f_{1}(\;0,\;a,b),&z_{0}&=f_{2}(\;0,\;a,b),\\\rho _{1}&=f_{1}(2\pi ,a,b),&z_{1}&=f_{2}(2\pi ,a,b).\end{aligned}}$

Soient $M_{0}$ le point dont les coordonnées sont

$x=\rho _{0},\quad y=0,\quad z=z_{0},$

et $\mathrm {M} _{1}$ celui dont les coordonnées sont

$x=\rho _{1},\quad y=0,\quad z=z_{1}.$

Ces deux points appartiennent tous deux au demi-plan des $xz$ situé du côté des $x$ positifs.

Le point $\mathrm {M} _{1}$ sera dit le conséquent de $\mathrm {M} _{0}.$

Ce qui justifie cette dénomination, c’est que, si l’on considère le faisceau des courbes qui satisfont aux équations différentielles (1) ; si, par le point $\mathrm {M} _{0},$ on fait passer une courbe et qu’on la prolonge jusqu’à ce qu’elle rencontre de nouveau le demi-plan $(y=0,\,x>0),$ cette nouvelle rencontre aura lieu en $\mathrm {M} _{1}.$

Si l’on trace dans ce demi-plan une figure quelconque $\mathrm {F} _{0},$ les conséquents des différents points de $\mathrm {F} _{0}$ formeront une figure $\mathrm {F} _{1},$ que l’on appellera la conséquente de $\mathrm {F} _{0}.$

Il est clair que $\rho _{1}$ et $z_{1}$ sont des fonctions continues de $\rho _{0}$ et de $z_{0}.$

Donc, la conséquente d’une courbe continue sera une courbe continue, celle d’une courbe fermée sera une courbe fermée, celle d’une aire $n$ fois connexe sera une aire $n$ fois connexe.

Supposons maintenant que les trois fonctions $\mathrm {X} ,$ $\mathrm {Y}$ et $\mathrm {Z}$ soient liées par la relation

${\frac {d\,\mathrm {MX} }{dx}}+{\frac {d\,\mathrm {MY} }{dy}}+{\frac {d\,\mathrm {MZ} }{dz}}=0,$

où $\mathrm {M}$ est une fonction positive et uniforme de $x,\,y,\,z.$

Les équations (1) admettront alors l’invariant intégral

$\int \mathrm {M} \,dx\,dy\,dz$

et les équations (2) admettront

$\int \mathrm {M} \,\rho \,d\rho \,d\omega \,dz.$

Considérons maintenant les équations

(3)

${\begin{aligned}{\frac {d\rho }{d\omega }}&={\frac {\mathrm {R} }{\Omega }},&{\frac {dz}{d\omega }}&={\frac {\mathrm {Z} }{\Omega }},&{\frac {d\omega }{d\omega }}&=1,\end{aligned}}$

où $\omega$ est regardé comme la variable indépendante.

Elles admettront évidemment l’invariant intégral

(4)

$\int \mathrm {M} \,\Omega \rho \,d\rho \,d\omega \,dz$

(Cf. n^o 253).

Comme $\mathrm {M} ,$ $\Omega$ et $\rho$ ont été supposés plus haut essentiellement positifs, c’est un invariant intégral positif.

Soient $\mathrm {F} _{0}$ une aire quelconque située dans le demi-plan

$(y=0,\quad x>0),$

et $\mathrm {F} _{1}$ sa conséquente.

Soient $\mathrm {J} _{0}$ l’intégrale

(5)

$\int \mathrm {M} \,\Omega \rho \,d\rho \,dz$

étendue à l’aire plane $\mathrm {F} _{0},$ et $\mathrm {J} _{1}$ la même intégrale étendue à l’aire plane $\mathrm {F} _{1}.$

Soit alors $\Phi _{0}$ le volume engendré par l’aire $\mathrm {F} _{0}$ quand on la fait tourner autour de l’axe des $z$ d’un angle infiniment petit $\varepsilon ,$ l’intégrale (4) étendue à $\Phi _{0}$ sera évidemment $\mathrm {J} _{0}\varepsilon .$

Soit de même $\Phi _{1}$ le volume engendré par l’aire $\mathrm {F} _{1}$ quand on la fait tourner autour de l’axe des $z$ d’un angle $\varepsilon ,$ l’intégrale (4) étendue à $\Phi _{1}$ sera $\mathrm {J} _{1}\varepsilon .$

L’invariant intégral (4) devant avoir même valeur pour $\Phi _{0}$ et pour $\Phi _{1},$ on doit avoir

$\mathrm {J} _{0}=\mathrm {J} _{1}.$

Ainsi, l’intégrale (5) a même valeur pour une aire quelconque et sa conséquente.

C’est une nouvelle forme de la propriété fondamentale des invariants intégraux.

306.Soit alors une courbe fermée $\mathrm {C} _{0}$ située dans le demi-plan $(y=0,\;x>0)$ et enveloppant une aire $\mathrm {F} _{0}.$ Soit $\mathrm {C} _{1}$ la conséquente de $\mathrm {C} _{0},$ ce sera aussi une courbe fermée qui enveloppera une aire $\mathrm {F} _{1},$ et cette aire $\mathrm {F} _{1}$ sera la conséquente de $\mathrm {F} _{0}.$

Si l’intégrale (5), étendue à $\mathrm {F} _{0}$ et à $\mathrm {F} _{1},$ a pour valeur $\mathrm {J} _{0}$ et $\mathrm {J} _{1},$ on aura

$\mathrm {J} _{0}=\mathrm {J} _{1},$

et il suit de là que $\mathrm {F} _{0}$ ne pourra être une partie de $\mathrm {F} _{1},$ et $\mathrm {F} _{1}$ une partie de $\mathrm {F} _{0}.$

Quatre hypothèses peuvent être faites sur la position relative des deux courbes fermées $\mathrm {C} _{0}$ et $\mathrm {C} _{1}.$

1^o $\mathrm {C} _{1}$ est intérieur à $\mathrm {C} _{0}\,;$

2^o $\mathrm {C} _{0}$ est intérieur à $\mathrm {C} _{1}\,;$

3^o Les deux courbes sont extérieures l’une à l’autre ;

4^o Les deux courbes se coupent.

L’équation $\mathrm {J} _{0}=\mathrm {J} _{1}$ exclut les deux premières de ces hypothèses.

Si, pour une raison quelconque, la troisième se trouve également exclue, on sera certain que les deux courbes se coupent.

Supposons, par exemple, que $\mathrm {X,\,Y,\,Z}$ dépendent d’un paramètre arbitraire $\mu ,$ et que, pour $\mu =0,$ $\mathrm {C} _{0}$ soit sa propre conséquente ; alors, pour les valeurs très petites de $\mu ,$ $\mathrm {C} _{0}$ différera très peu de $\mathrm {C} _{1}\,;$ il ne pourra donc pas arriver que les deux courbes $\mathrm {C} _{0}$ et $\mathrm {C} _{1}$ soient extérieures l’une à l’autre, et il faudra qu’elles se coupent.

Courbes invariantes.

307.J’appellerai courbe invariante toute courbe qui sera sa propre conséquente.

Il est aisé de former des courbes invariantes ; soient, en effet, $\mathrm {M} _{0}$ un point quelconque du demi-plan, $\mathrm {M} _{1}$ son conséquent ; joignons $\mathrm {M} _{0}$ à $\mathrm {M} _{1}$ par un arc de courbe quelconque $\mathrm {C} _{0}\,;$ soit $\mathrm {C} _{1}$ le conséquent de $\mathrm {C} _{0},$ $\mathrm {C} _{2}$ celui de $\mathrm {C} _{1},$ et ainsi de suite. L’ensemble des arcs de courbe $\mathrm {C} _{0},$ $\mathrm {C} _{1},$ $\mathrm {C} _{2},\,\ldots$ constituera évidemment une courbe invariante.

Mais nous serons amenés aussi à envisager des courbes invariantes dont la génération sera plus naturelle.

Supposons que les équations (1) admettent une solution périodique. Soient

(6)

${\begin{aligned}x&=\varphi _{1}(t),&y&=\varphi _{2}(t),&z&=\varphi _{3}(t)\end{aligned}}$

les équations de cette solution périodique, de telle façon que les fonctions $\varphi _{i}$ soient périodiques en $t,$ de période $\mathrm {T} .$

Je suppose que, quand $t$ augmente de $\mathrm {T} ,$ $\omega$ augmente de $2\pi .$

Les équations (6) représentent une courbe ; soit $\mathrm {M} _{0}$ le point où cette courbe coupe le demi-plan ; ce point $\mathrm {M} _{0}$ sera évidemment son propre conséquent.

Supposons maintenant qu’il existe des solutions asymptotiques très voisines de la solution périodique (6). Soient

(7)

${\begin{aligned}x&=\Phi _{1}(t),&y&=\Phi _{2}(t),&z&=\Phi _{3}(t)\end{aligned}}$

les équations de ces solutions.

Les fonctions $\Phi _{i}$ seront développables suivant les puissances de $\mathrm {A} e^{\alpha t},$ les coefficients étant eux-mêmes des fonctions périodiques de $t.$ Dans cette expression, $\alpha$ est un exposant caractéristique, $\mathrm {A}$ est une constante d’intégration.

Dans les équations (7), les trois coordonnées $x,\,y,\,z$ se trouvent donc exprimées en fonction de deux paramètres, $\mathrm {A}$ et $t\,;$ ces équations représentent donc une surface que l’on peut appeler la surface asymptotique. Cette surface asymptotique va passer par la courbe (6) ; puisque les équations (7) se réduisent aux équations (6), quand on y fait $\mathrm {A} =0.$

La surface asymptotique va couper le demi-plan suivant une certaine courbe qui passe par le point $\mathrm {M} _{0}$ et qui est manifestement une courbe invariante.

308.Considérons une courbe invariante $\mathrm {K} .$ Je suppose que $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z}$ dépendent du paramètre $\mu ,$ ainsi d’ailleurs que la courbe $\mathrm {K} .$

Je suppose que pour $\mu =0,$ la courbe $\mathrm {K}$ soit fermée, mais qu’elle cesse de l’être pour les petites valeurs de $\mu .$

Soit $\mathrm {A} _{0}$ un point de $\mathrm {K} .$ La position de ce point dépendra de $\mu \,;$ pour $\mu =0,$ la courbe $\mathrm {K}$ est fermée, de sorte que, après avoir parcouru cette courbe à partir de $\mathrm {A} _{0},$ on revient au point $\mathrm {A} _{0}$ ; si $\mu$ est très petit, il n’en sera plus de même, mais on reviendra passer très près de $\mathrm {A} _{0}\,;$ il y aura donc sur la courbe $\mathrm {K}$ un arc de courbe différent de celui où se trouve $\mathrm {A} _{0},$ mais qui viendra passer très près de $\mathrm {A} _{0}.$ Soit $\mathrm {B} _{0}$ le point de cet arc de courbe qui est le plus voisin de $\mathrm {A} _{0}.$

Je joins $\mathrm {A} _{0}\mathrm {B} _{0}.$

Soient $\mathrm {A} _{1}$ et $\mathrm {B} _{1}$ les conséquents de $\mathrm {A} _{0}$ et $\mathrm {B} _{0}\,;$ ces deux points se trouveront sur $\mathrm {K} \,;$ soit $\mathrm {A} _{1}\mathrm {B} _{1}$ la courbe conséquente de la petite droite $\mathrm {A} _{0}\mathrm {B} _{0}.$

Nous aurons à envisager la courbe fermée $\mathrm {C} _{0}$ qui se compose de l’arc $\mathrm {A} _{0}\mathrm {MB} _{0}$ de la courbe $\mathrm {K}$ compris entre $\mathrm {A} _{0}$ et $\mathrm {B} _{0}$ et de la petite droite $\mathrm {A} _{0}\mathrm {B} o.$ Quelle sera sa conséquente ?

Supposons, pour fixer les idées, que les quatre points $\mathrm {A} _{1},$ $\mathrm {A} _{0},$ $\mathrm {B} _{1},$ $\mathrm {B} _{0}$ se succèdent sur $\mathrm {K}$ dans l’ordre $\mathrm {A} _{1}\mathrm {A} _{0}\mathrm {B} _{1}\mathrm {B} _{0}.$

La conséquente $\mathrm {C} _{1}$ de $\mathrm {C} _{0}$ se composera de l’arc $\mathrm {A} _{1}\mathrm {MB} _{1}$ de la courbe $\mathrm {K}$ et du petit arc $\mathrm {A} _{1}\mathrm {B} _{1},$ conséquent de la petite droite $\mathrm {A} _{0}\mathrm {B} _{0}.$

On peut faire plusieurs hypothèses :

1^o Le petit quadrilatère curviligne $\mathrm {A} _{0}\mathrm {B} _{0}\mathrm {A} _{1}\mathrm {B} _{1}$ est convexe, je veux dire qu’aucun de ses côtés curvilignes ne présente de point double et que les seuls points communs à deux côtés sont les sommets. Dans cette hypothèse, la courbe se présenterait comme l’indique l’une des deux figures suivantes

Fig. 1.	Fig.2

Cette hypothèse doit être rejetée, car il est manifeste que l’intégrale $\mathrm {J}$ est plus grande dans le cas de la fig. 1 pour $\mathrm {C} _{1}$ que pour $\mathrm {C} _{0},$ et plus petite dans le cas de la fig. 2.

2^o L’arc $\mathrm {A} _{0}\mathrm {A} _{1}$ ou $\mathrm {B} _{0}\mathrm {B} _{1}$ a un point double. — S’il en était ainsi l’arc qui joint un point quelconque de la courbe à son premier conséquent ; nous supposerons qu’il n’en est pas ainsi ; et, en effet, cette circonstance ne se présentera dans aucune des applications que j’ai en vue ; elle ne s’appliquera pas, en particulier, dans le cas de la courbe invariante engendrée par une surface asymptotique ainsi que je l’ai expliqué à la fin du numéro précédent. Il est aisé de constater, en effet, que la surface asymptotique ne présente pas de ligne double si l’on se borne à la portion de cette surface qui correspond aux petites valeurs des quantités que j’ai appelées plus haut $\mathrm {A} e^{\alpha t}.$

D’autre part, la droite $\mathrm {A} _{0}\mathrm {B} _{0}$ n’a pas de point double, et il doit en être de même de sa conséquente $\mathrm {A} _{1}\mathrm {B} _{1}.$ En résumé, nous supposerons que les quatre côtés de notre quadrilatère n’ont pas de point double.

3^o L’arc $\mathrm {A} _{0}\mathrm {A} _{1}$ coupe l’arc $\mathrm {B} _{0}\mathrm {B} _{1}.$ — (Ce cas contient comme cas particulier celui où la courbe K serait fermée.) Nos courbes présentent alors l’aspect de la fig. 3.

Fig. 3.

4^o L’arc $\mathrm {A} _{0}\mathrm {B} _{0}$ coupe son conséquent $\mathrm {A} _{1}\mathrm {B} _{1}.$ — Nos courbes présenteraient alors l’aspect de la fig. 4.

Il y a des cas où l’hypothèse doit être rejetée. Supposons, par exemple, que $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z}$ dépendent d’un paramètre $\mu \,;$ que pour $\mu =0$ la courbe $\mathrm {K}$ soit fermée et que chacun de ses points soit son propre conséquent, de telle façon que pour $\mu =0$ les quatre sommets du quadrilatère se confondent.

Alors les quatre distances $\mathrm {A} _{0}\mathrm {B} _{0},$ $\mathrm {A} _{1}\mathrm {B} _{1},$ $\mathrm {A} _{1}\mathrm {A} _{0},$ $\mathrm {B} _{1}\mathrm {B} _{0}$ seront des infiniment petits si $\mu$ est l’infiniment petit principal. Supposons que $\mathrm {A} _{1}\mathrm {A} _{0}$ soit un infiniment petit d’ordre $p,$ $\mathrm {A} _{0}\mathrm {B} _{0}$ un infiniment petit d’ordre $q,$ et que $q$ soit plus grand que $p.$

Fig. 4.

Comme $\mathrm {A} _{1}\mathrm {B} _{1}$ est le conséquent de $\mathrm {A} _{0}\mathrm {B} _{0},$ la longueur de l’arc $\mathrm {A} _{1}\mathrm {B} _{1}$ devra être d’ordre $q.$ Soit alors $\mathrm {C}$ l’un des points d’intersection de $\mathrm {A} _{0}\mathrm {B} _{0}.$ Dans le triangle mixtiligne dont deux côtés sont les droites $\mathrm {A} _{1}\mathrm {A} _{0}$ et $\mathrm {A} _{0}\mathrm {C}$ et le troisième côté l’arc de courbe $\mathrm {A} _{1}\mathrm {C}$ faisant partie de $\mathrm {A} _{1}\mathrm {B} _{1}\,;$ le côté $\mathrm {A} _{1}\mathrm {C}$ est plus grand que la différence des deux autres ; il devrait donc être d’ordre $p$ et nous avons vu qu’il doit être d’ordre $q.$

L’hypothèse doit donc être rejetée.

5^o Deux côtés adjacents du quadrilatère se coupent, par exemple $\mathrm {A} _{1}\mathrm {A} _{0}$ et $\mathrm {A} _{1}\mathrm {B} _{1}.$ — Il faut alors que $\mathrm {A} _{0}\mathrm {B} _{0},$ qui est l’antécédent de $\mathrm {A} _{1}\mathrm {B} _{1},$ coupe lui-même $\mathrm {K} \,;$ si $\mathrm {A} _{0}'$ est l’intersection de $\mathrm {A} _{0}\mathrm {B} _{0}$ avec $\mathrm {K}$ et $\mathrm {A} _{1}'$ celle de $\mathrm {A} _{1}\mathrm {B} _{1}$ avec l’arc $\mathrm {A} _{0}\mathrm {A} _{1},$ $\mathrm {A} _{1}'$ sera le conséquent de $\mathrm {A} _{0}'$ et nous tomberons sur la figure suivante

Fig. 5.

Il est manifeste que $\mathrm {A} _{0}'$ et $\mathrm {A} _{1}'$ peuvent jouer le même rôle que $\mathrm {A} _{0}$ et $\mathrm {A} _{1}$ et que l’on retombe sur le premier cas.

Cette nouvelle hypothèse doit donc être rejetée.

En résumé les deux arcs $\mathrm {A} _{0}\mathrm {A} _{1}$ et $\mathrm {B} _{0}\mathrm {B} _{1}$ se couperont toutes les fois que pour une raison ou pour une autre les hypothèses 2^o et 4^o devront être rejetées.

Il resterait à examiner le cas où les points $\mathrm {A} _{1},$ $\mathrm {A} _{0},$ $\mathrm {B} _{1},$ $\mathrm {B} _{0}$ se suivraient sur $\mathrm {K}$ dans un ordre différent. Les ordres $\mathrm {B} _{1}\mathrm {B} _{0}\mathrm {A} _{1}\mathrm {A} _{0},$ $\mathrm {B} _{0}\mathrm {B} _{1}\mathrm {A} _{0}\mathrm {A} _{1},$ $\mathrm {A} _{0}\mathrm {A} _{1}\mathrm {B} _{0}\mathrm {B} _{1}$ ne diffèrent pas essentiellement de celui que nous venons d’étudier.

Les ordres tels que $\mathrm {A} _{1}\mathrm {B} _{1}\mathrm {B} _{0}\mathrm {A} _{0},$ $\mathrm {A} _{1}\mathrm {B} _{0}\mathrm {B} _{1}\mathrm {A} _{0},$ $\mathrm {A} _{1}\mathrm {B} _{0}\mathrm {A} _{0}\mathrm {B} _{1},\,\ldots$ ne se présenteront pas dans les applications qui vont suivre ; nous supposerons toujours en effet que, si $\mu$ est très petit, les distances $\mathrm {A} _{0}\mathrm {A} _{1}$ et $\mathrm {B} _{0}\mathrm {B} _{1}$ sont très petites par rapport à la longueur des arcs $\mathrm {A} _{0}\mathrm {MB} _{0}$ ou $\mathrm {A} _{1}\mathrm {MB} _{1}.$

Il reste l’ordre $\mathrm {A} _{1}\mathrm {A} _{0}\mathrm {B} _{0}\mathrm {B} _{1}$ ou les ordres équivalents ; nous n’en parlerons pas non plus ; il est clair que, s’il se présente, il y aura sur l’arc $\mathrm {A} _{0}\mathrm {MB} _{0}$ un point qui sera son propre conséquent.

309.Supposons par exemple que les équations (1) admettent une solution périodique

(6)

${\begin{aligned}x&=\varphi _{1}(t),&y&=\varphi _{2}(t),&z&=\varphi _{3}(t)\end{aligned}}$

et des solutions asymptotiques

(7)

${\begin{aligned}x&=\Phi _{1}(t),&y&=\Phi _{2}(t),&z&=\Phi _{3}(t).\end{aligned}}$

Supposons que les équations (1) dépendent d’un paramètre très petit $\mu$ et que $\mathrm {X,\,Y,\,Z}$ soient développables suivant les puissances de ce paramètre.

Supposons que, pour $\mu =0,$ les solutions asymptotiques (7) se réduisent à des solutions périodiques. Voici comment cela pourra se faire. Nous avons dit que les $\Phi _{i}$ sont développables suivant les puissances de $\mathrm {A} e^{\alpha t},$ les coefficients étant eux-mêmes des fonctions périodiques de $t.$ Mais l’exposant $\alpha$ dépend de $\mu \,;$ supposons qu’il s’annule pour $\mu =0\,;$ alors pour $\mu =0$ les fonctions $\Phi _{i}$ deviendront des fonctions périodiques de $t$ et les solutions (7) se réduiront à des solutions périodiques.

La surface asymptotique va couper le demi-plan suivant une certaine courbe $\mathrm {C} _{0}$ qui passe par le point $\mathrm {M} _{0},$ intersection du demi-plan avec la courbe gauche (6).

La courbe $\mathrm {C} _{0}$ est manifestement invariante, comme je l’ai dit à la fin du n^o 307 ; pour $\mu =0,$ chacun des points de $\mathrm {C} _{0}$ est son propre conséquent.

Je supposerai de plus que, pour $\mu =0,$ la courbe $\mathrm {C} _{0}$ est fermée.

Reportons-nous au Chapitre VII, tome I ; nous avons vu aux n^os 107 et suivants que, dans le cas de la Dynamique, les exposants caractéristiques sont développables suivant les puissances de ${\sqrt {\overset {}{\mu }}}$ et sont d’ailleurs deux à deux égaux et de signe contraire. Nous supposerons qu’il en est ainsi.

Nous avons alors en réalité deux surfaces asymptotiques correspondant aux deux exposants égaux et de signe contraire $\alpha$ et $-\alpha \,;$ nous avons donc deux courbes $\mathrm {C} _{0}$ qui iront se couper au point $\mathrm {M} _{0}.$

Nous distinguerons quatre branches de courbe

$\mathrm {C} _{0}',\quad \mathrm {C} _{0}'',\quad \mathrm {C} _{1}',\quad \mathrm {C} _{1}''$

aboutissant toutes quatre au point $\mathrm {M} _{0}\,;$ $\mathrm {C} _{0}'$ et $\mathrm {C} _{0}''$ correspondront à l’exposant $\alpha ,$ $\mathrm {C} _{1}'$ et $\mathrm {C} _{1}''$ à l’exposant $-\alpha .$

Fig. 6.

Ces diverses branches de la courbe sont représentées sur la fig. 6. La branche $\mathrm {C} _{0}'$ est la branche $\mathrm {M} _{0}\mathrm {P} _{0}\mathrm {P} _{1}\mathrm {A} _{0}\mathrm {A} _{1},$ la branche $\mathrm {C} _{0}''$ est la branche $\mathrm {M} _{0}\mathrm {E} _{0}\mathrm {E} _{1}\,;$ la branche $\mathrm {C} _{1}'$ est la branche $\mathrm {M} _{0}\mathrm {Q} _{1}\mathrm {Q} _{0}$ et la branche $\mathrm {C} _{1}''$ est la branche $\mathrm {M} _{0}\mathrm {R} _{1}\mathrm {R} _{0}\mathrm {B} _{1}\mathrm {B} _{0}.$

Ces quatre branches de courbe sont évidemment invariantes.

Maintenant, pour $\mu =0,$ $\mathrm {C} _{0}'$ se confond avec $\mathrm {C} _{1}',$ $\mathrm {C} _{0}''$ avec $\mathrm {C} _{1}''$ et (si nous supposons que, pour $\mu =0,$ la courbe $\mathrm {C} _{0}$ que nous appellerons alors $\mathrm {C} _{0}^{0}$ est fermée) ces quatre branches de courbe iront s’appliquer sur la courbe fermée $\mathrm {C} _{0}^{0}.$

On peut déduire de là que, pour $\mu$ très petit, ces branches de courbe différeront peu les unes des autres ; que $\mathrm {C} _{0}'$ s’écartera peu de $\mathrm {C} _{1}',$ $\mathrm {C} _{0}''$ de $\mathrm {C} _{1}''$ et que $\mathrm {C} _{0}'$ suffisamment prolongé ira passer très près de $\mathrm {C} _{1}''$ suffisamment prolongé.

J’ai marqué sur la figure divers points de ces branches de courbe et leurs conséquents. Ainsi $\mathrm {A} _{1},$ $\mathrm {B} _{1},$ $\mathrm {E} _{1},$ $\mathrm {P} _{1},$ $\mathrm {Q} _{1},$ $\mathrm {R} _{1}$ sont respectivement les conséquents de $\mathrm {A} _{0},$ $\mathrm {B} _{0},$ $\mathrm {E} _{0},$ $\mathrm {P} _{0},$ $\mathrm {Q} _{0},\,\mathrm {R} _{0}.$

Ce que nous remarquerons d’abord, c’est que les points $\mathrm {A} _{1},$ $\mathrm {A} _{0},$ $\mathrm {B} _{1},$ $\mathrm {B} _{0}$ se succèdent bien (comme nous l’avons supposé au début du n^o 308) dans l’ordre $\mathrm {A} _{1}\mathrm {A} _{0}\mathrm {B} _{1}\mathrm {B} _{0}$ quand on parcourt de $\mathrm {A} _{1}$ à $\mathrm {B} _{0}$ la courbe invariante formée des deux branches $\mathrm {C} _{0}'$ et $\mathrm {C} _{1}''.$

Cette courbe invariante n’est pas fermée, mais elle diffère peu de la courbe fermée $\mathrm {C} _{0}^{0}.$

Examinons, en ce qui la concerne, les cinq hypothèses du n^o 308. La première, comme nous l’avons vu, doit toujours être rejetée. La seconde ne se présentera pas non plus.

Elle ne pourrait se présenter, en effet, que si la surface asymptotique (7) avait une ligne double.

Nous avons dit que les $\Phi _{i}$ sont développables suivant les puissances de $\mathrm {A} e^{\alpha t}\,;$ soit donc

$\Phi _{i}=\Phi _{i}^{0}+\mathrm {A} e^{\alpha t}\Phi _{i}^{1}+\mathrm {A} ^{2}e^{2\alpha t}\Phi _{i}^{2}+\ldots .$

Si notre surface avait une ligne double, cette ligne double devrait satisfaire aux équations (1) ; en effet, la surface asymptotique est engendrée par une infinité de lignes satisfaisant à ces équations de telle sorte que, si deux nappes de cette surface venaient à se couper, l’intersection ne pourrait être autre chose qu’une de ces lignes.

Comme $\Phi _{i}$ dépend à la fois du temps $t$ et du paramètre $\mathrm {A} ,$ nous mettrons ce fait en évidence en écrivant

$\Phi _{i}=\Phi _{i}(t,\mathrm {A} ).$

S’il y avait une ligne double, nous devrions avoir les trois identités

$\Phi _{i}(t,\mathrm {A} )=\Phi _{i}(t',\mathrm {B} )\qquad (i=1,\,2,\,3),$

où $\mathrm {A}$ et $\mathrm {B}$ sont deux constantes et où $t'$ est une fonction de $t\,;$ ces trois identités devraient subsister quel que soit $t.$

En différentiant, on aura

${\frac {d\Phi _{i}}{dt}}={\frac {d\Phi _{i}}{dt'}}{\frac {dt'}{dt}}\cdot$

Mais, en vertu des équations (1), on aura

${\frac {d\Phi _{1}}{dt}}=\mathrm {X} \left[\Phi _{1}(t,\mathrm {A} ),\,\Phi _{2}(t,\mathrm {A} ),\,\Phi _{3}(t,\mathrm {A} )\right]$

et de même

${\frac {d\Phi _{1}}{dt'}}=\mathrm {X} \left[\Phi _{1}(t',\mathrm {B} ),\,\Phi _{2}(t',\mathrm {B} ),\,\Phi _{3}(t',\mathrm {B} )\right],$

d’où

${\begin{aligned}{\frac {d\Phi _{i}}{dt}}&={\frac {d\Phi _{i}}{dt'}},&{\frac {dt'}{dt}}&=1,\end{aligned}}$

d’où

$t'=t+h,$

$h$ étant une constante.

On tirerait de là

$\Phi _{i}^{0}(t)+\mathrm {A} e^{\alpha t}\Phi _{i}^{1}(t)+\mathrm {A} ^{2}e^{2\alpha t}\Phi _{i}^{2}(t)=\Phi _{i}^{0}(t+h)+\mathrm {C} e^{\alpha t}\Phi _{i}^{1}(t+h)+\ldots ,$

où

$\mathrm {C} =\mathrm {B} e^{\alpha h}.$

L’identité devant être vraie pour $t=-\infty ,$ d’où

$\mathrm {A} e^{\alpha t}=\mathrm {C} e^{\alpha t}=0,$

il vient

$\Phi _{i}^{0}(t)=\Phi _{i}^{0}(t+h),$

d’où $h=o,$ d’où

$\Phi _{i}^{0}(t)+\mathrm {A} e^{\alpha t}\Phi _{i}^{1}(t)+\ldots =\Phi _{i}^{0}(t)+\mathrm {C} e^{\alpha t}\Phi _{i}^{1}(t)+\ldots$

ou

$\mathrm {A} \Phi _{i}^{0}(t)+\mathrm {A} ^{2}e^{\alpha t}\Phi _{i}^{2}(t)+\ldots =\mathrm {C} \Phi _{i}^{0}(t)+\mathrm {C} ^{2}e^{\alpha t}\Phi _{i}^{2}(t)+\ldots$

ou, en faisant encore $t=-\infty ,$

$\mathrm {A} =\mathrm {C} =\mathrm {B} .$

Les deux valeurs $\mathrm {A}$ et $\mathrm {B}$ étant égales, il n’y a pas de Ligne double.

C. Q. F. D.

La troisième hypothèse est celle qu’il convient d’adopter.

Passons à la quatrième ; pour voir si elle doit être rejetée, il faut chercher à se rendre compte de l’ordre de grandeur des distances $\mathrm {A} _{1}\mathrm {A} _{0}$ et $\mathrm {A} _{0}\mathrm {B} _{0}\,:$ c’est ce que nous ferons dans les diverses applications qui vont suivre.

Enfin, la cinquième hypothèse se ramène toujours à la première, comme nous l’avons vu.

Extension des résultats précédents.

310.Nous avons fait plus haut sur les équations (1) des hypothèses très particulières ; mais toutes ne sont pas également nécessaires.

Considérons, en effet, un domaine $\mathrm {D}$ simplement connexe et faisant partie du demi-plan $(y=0,x>0),$ et supposons que l’on sache d’une manière quelconque que, si le point $(x,y,z)$ se trouve à l’origine du temps en un point $\mathrm {M} _{0}$ de ce domaine, $\omega$ va en croissant constamment de 0 à $2\pi$ quand $t$ croît de 0 à $t_{0}\;;$ de telle façon que la courbe satisfaisant aux équations (1) et passant par le point $\mathrm {M} _{0},$ en la supposant prolongée depuis ce point $\mathrm {M} _{0}$ jusqu’à sa nouvelle rencontre avec le demi-plan, n’est jamais tangente à un plan passant par l’axe des $z.$

Alors on pourra définir, comme au n^o 305, le conséquent du point $\mathrm {M} _{0},$ et il est clair que tout ce qui précède sera encore applicable aux figures qui se trouvent à l’intérieur du domaine $\mathrm {D} .$

Il ne sera pas nécessaire que les courbes qui satisfont aux équations (1) et qui viennent rencontrer le demi-plan en dehors de $\mathrm {D}$ soient assujetties à ne jamais être tangentes à un plan passant par l’axe des $z.$ Il ne sera pas nécessaire non plus que $x=y=0$ soit une solution des équations (1).

Alors, si $\mathrm {C} _{0}$ est une courbe fermée intérieure à $\mathrm {D}$ et si $\mathrm {C} _{1}$ est sa conséquente, les deux courbes seront extérieures l’une à l’autre ou se couperont.

Les résultats du n^o 308 seront également applicables aux courbes invariantes qui ne sortiront pas du domaine $\mathrm {D} \,;$ et, si même une courbe invariante sort du domaine $\mathrm {D}$ quand elle est suffisamment prolongée, les résultats seront encore applicables à la portion de cette courbe qui est intérieure à ce domaine.

311.Considérons maintenant, au lieu d’un domaine plan $\mathrm {D} ,$ une aire courbe $\mathrm {S}$ simplement connexe. Par un point $\mathrm {M} _{0}$ de cette aire courbe faisons passer une courbe $\gamma$ satisfaisant aux équations (1) et prolongeons cette courbe jusqu’à ce qu’elle rencontre de nouveau $\mathrm {S} \,;$ le nouveau point d’intersection $\mathrm {M} _{1}$ pourra encore s’appeler le conséquent de $\mathrm {M} _{0}.$

Si nous considérons deux points, $\mathrm {M} _{0}$ et $\mathrm {M} _{0}',$ très voisins l’un de l’autre, leurs conséquents seront, en général, très voisins l’un de l’autre ; il y aurait exception si le point $\mathrm {M} _{1}$ se trouvait sur le bord de $\mathrm {S} ,$ ou si la courbe $\gamma$ touchait la surface au point $\mathrm {M} _{1}$ ou au point $\mathrm {M} _{0}.$ Sauf ces cas d’exception, les coordonnées de $\mathrm {M} _{1}$ sont des fonctions analytiques des coordonnées de $\mathrm {M} _{0}.$

Pour éviter ces cas d’exception, je considérerai un domaine $\mathrm {D}$ faisant partie de $\mathrm {S}$ et tel que la courbe $\gamma ,$ issue d’un point $\mathrm {M} _{0}$ intérieur à $\mathrm {D} ,$ vienne recouper $\mathrm {S}$ en un point $\mathrm {M} _{1}$ qui ne vienne jamais sur le bord de $\mathrm {S} \,;$ tel aussi que la courbe $\gamma$ ne touche $\mathrm {S}$ ni en $\mathrm {M} _{0},$ ni en $\mathrm {M} _{1}.$ Je supposerai enfin que ce domaine $\mathrm {D}$ est simplement connexe.

Adoptons un système particulier de coordonnées que j’appellerai, par exemple, $\xi ,$ $\eta$ et $\zeta$ et pour lesquelles je supposerai seulement ce qui suit :

1^o Quand $|\xi |$ et $|\eta |$ seront plus petits que 1, les coordonnées rectangulaires $x,$ $y$ et $z$ seront des fonctions analytiques et uniformes de $\xi ,$ $\eta$ et $\zeta ,$ qui seront périodiques de période $2\pi$ par rapport à $\zeta .$

2^o À un point $(x,y,z)$ de l’espace ne pourra correspondre plus d’un système de valeurs de $\xi ,\eta ,\zeta$ tel que

(λ)

$|\xi |<1,\quad |\eta |<1,\quad 0<\zeta <2\pi .$

3^o Quand on fait $\zeta =0,$ ou $\zeta =2\pi$ et qu’on fait varier $\xi$ et $\eta$ de $-1$ à $+1,$ le point $x,y,z$ décrit la surface $\mathrm {S} ,$ ou une portion de cette surface comprenant le domaine $\mathrm {D} .$

4^o Des conditions (1) et (2) il résulte que le déterminant fonctionnel $\Delta$ de $\xi ,\eta ,\zeta$ par rapport à $x,y,z$ n’est jamais infini ni nul quand les inégalités (λ) sont remplies.

5^o On peut transformer les équations (1) en les mettant sous la forme

(1 bis)

${\begin{aligned}{\frac {d\xi }{dt}}&=\Xi ,&{\frac {d\eta }{dt}}&=\mathrm {H} ,&{\frac {d\zeta }{dt}}&=\mathrm {Z} ^{\star }.\end{aligned}}$

Je supposerai que $\mathrm {Z} ^{\star }$ reste positif pour

$|\xi |<1,\quad |\eta |<1,\quad \zeta =0.$

Les équations (1 bis) admettront l’invariant intégral

$\int {\frac {\mathrm {M} }{\Delta }}\,d\xi \,d\eta \,d\zeta ,$

et les équations

(3 bis)

${\begin{aligned}{\frac {d\xi }{d\zeta }}&={\frac {\Xi }{\mathrm {Z} ^{\star }}},&{\frac {d\eta }{d\zeta }}&={\frac {\mathrm {H} }{\mathrm {Z} ^{\star }}},&{\frac {d\zeta }{d\zeta }}&=1\end{aligned}}$

admettront l’invariant intégral

$\int {\frac {\mathrm {MZ} ^{\star }}{\Delta }}\,d\xi \,d\eta \,d\zeta$

Soit $\mathrm {F} _{0}$ une figure quelconque faisant partie de $\mathrm {D}$ et $\mathrm {F} ,$ sa conséquente ; supposons que les différents points de $\mathrm {F} _{0}$ et de $\mathrm {F} _{1}$ se déplacent de telle façon que $\xi$ et $\eta$ restent constants et que $\zeta$ croisse de 0 à $\varepsilon ,$ $\varepsilon$ étant très petit ; la figure $\mathrm {F} _{0}$ engendrera un volume $\Phi _{0},$ et la figure $\mathrm {F} _{1}$ engendrera un volume $\Phi _{1}\,;$ l’intégrale

$\int {\frac {\mathrm {MZ} ^{\star }}{\Delta }}\,d\xi \,d\eta \,d\zeta =\varepsilon \int {\frac {\mathrm {MZ} ^{\star }}{\Delta }}\,d\xi \,d\eta$

aura même valeur pour $\Phi _{0}$ et pour $\Phi _{1}\,;$ donc l’intégrale double

$\int {\frac {\mathrm {MZ} ^{\star }}{\Delta }}\,d\xi \,d\eta ,$

analogue à l’intégrale (5) du n^o 305, aura même valeur pour $\mathrm {F} _{0}$ et $\mathrm {F} _{1}.$ Elle est d’ailleurs essentiellement positive.

Il résulte de là que les résultats du n^o 306 sont applicables aux courbes fermées $\mathrm {C} _{0}$ situées à l’intérieur de $\mathrm {D} ,$ et que ceux du n^o 308 sont applicables aux courbes invariantes $\mathrm {K} ,$ ou du moins à la portion de ces courbes qui est à l’intérieur de $\mathrm {D} .$

Même une courbe invariante sort du domaine $\mathrm {D}$ quand elle est suffisamment prolongée, les résultats seront encore applicables à la portion de cette courbe qui est intérieure à ce domaine.

Application aux équations de la Dynamique.

312.Soit $\mathrm {F}$ une fonction des quatre variables $x_{1},\,x_{2},\,y_{1},\,y_{2}\,;$ formons les équations canoniques

(1)

${\begin{aligned}{\frac {dx_{i}}{dt}}&={\frac {d\mathrm {F} }{dy_{i}}},&{\frac {dy_{i}}{dt}}&=-{\frac {d\mathrm {F} }{dx_{i}}}\cdot \end{aligned}}$

Je supposerai, comme je le fais d’ordinaire :

1^o Que $\mathrm {F}$ est une fonction périodique de $y_{1}$ et $y_{2}\,;$

2^o Que $\mathrm {F}$ dépend d’un paramètre $\mu$ et est développable suivant les puissances de ce paramètre sous la forme

$\mathrm {F} =\mathrm {F} _{0}+\mu \,\mathrm {F} _{1}+\mu ^{2}\,\mathrm {F} _{2}+\ldots ;$

3^o Que $\mathrm {F} _{0}$ est fonction seulement de $x_{1}$ et de $x_{2}.$

Cela posé, nous aurons l’intégrale

(2)

$\mathrm {F} =\mathrm {C} ,$

$\mathrm {C}$ étant une constante.

Cela posé, donnons à $\mathrm {C}$ une valeur déterminée une fois pour toutes et soit $\mathrm {M}$ un point mobile dont les coordonnées rectangulaires sont

$[1+\varphi (x_{1})\cos y_{1}]\cos y_{2},\quad [1+\varphi (x_{1})\cos y_{1}]\sin y_{2},\quad \varphi (x_{1})\sin y_{1}.$

La fonction $\varphi (x_{1})$ est une fonction de $x_{1}$ que je me réserve de déterminer plus complètement dans la suite.

Supposons d’abord que $\mathrm {F} ,$ qui dépendra de $x_{2}$ d’une manière quelconque, soit développable suivant les puissances croissantes de $x_{1}\cos {y_{1}}$ et $x_{1}\sin {y_{1}}.$ Il en résultera que, pour $x_{1}=0,$ la fonction $\mathrm {F}$ ne dépendra plus de $y_{1}$ et, d’autre part, que la fonction $\mathrm {F}$ ne changera pas quand on changera $x_{1}$ en $-x_{1}$ et $y_{1}$ en $y_{1}+\pi .$ Nous supposerons alors que $\varphi (x_{1})$ est une fonction impaire de $x_{1}$ qui croît de 0 à 1 and $x_{1}$ croît de 0 à $+\infty \,;$ on pourra prendre par exemple

$\varphi (x_{1})={\frac {x_{1}}{\sqrt {1+x_{1}^{2}}}}\cdot$

Si l’on adopte cette hypothèse, le point $\mathrm {M}$ sera toujours à l’intérieur d’un tore de rayon 1, tangent à l’axe des $z.$

À chaque point $\mathrm {M}$ intérieur à ce tore, correspondront une infinité de systèmes de valeurs de $x_{1},$ $y_{1}$ et $y_{2}\,;$ mais ces systèmes ne seront pas essentiellement distincts les uns des autres, puisqu’on passe de l’un à l’autre en augmentant $y_{1}$ ou $y_{2}$ d’un multiple de $2\pi$ ou en changeant $x_{1}$ en $-x_{1}$ et $y_{1}$ en $y_{1}+\pi .$

Si l’on se donne $x_{1},\,y_{1}$ et $y_{2},$ $x_{2}$ s’en déduira à l’aide de l’équation(2). Supposons que les variables $x$ et $y$ varient conformément aux équations (1), le point $\mathrm {M}$ correspondant décrira une certaine courbe que j’appellerai trajectoire.

Par chaque point intérieur au tore passe une trajectoire et une seule.

Il est aisé de voir quelle est la forme de ces trajectoires pour $\mu =0.$

Pour $\mu =0,$ les équations différentielles se réduisent à

${\begin{aligned}{\frac {dx_{i}}{dt}}&=0,&{\frac {dy_{i}}{dt}}&=-{\frac {d\mathrm {F} _{0}}{dx_{i}}}\cdot \end{aligned}}$

Les $x_{i}$ sont donc des constantes, ce qui montre que nos trajectoires sont situées sur des tores, et les $y_{i}$ sont des fonctions linéaires du temps ; car

$-{\frac {d\mathrm {F} _{0}}{dx_{i}}}=n_{i},$

ne dépendant que des $x_{i},$ est une constante.

Si le rapport $n_{1}:n_{2}$ est commensurable, les trajectoires sont des courbes fermées ; elles ne sont pas fermées, au contraire, si ce rapport est incommensurable.

Soient $m_{1},\,m_{2},\,p_{1},\,p_{2}$ quatre entiers tels que

$m_{1}p_{2}-m_{2}p_{1}=1\,;$

posons

${\begin{alignedat}{5}y_{1}'&=&{}{}&m_{1}y_{1}&{}+{}&m_{2}y_{2},\\y_{2}'&=&{}{}&p_{1}y_{1}&{}+{}&p_{2}y_{2},\\x_{1}'&=&{}{}&p_{2}x_{1}&{}-{}&p_{1}x_{2},\\x_{2}'&=&{}-{}&m_{2}x_{1}&{}+{}&m_{1}x_{2}.\end{alignedat}}$

L’identité

$x_{1}'y_{1}'+x_{2}'y_{2}'=x_{1}y_{1}+x_{2}y_{2}$

montre qu’en passant des variables $x_{i},\,y_{i}$ aux variables $x_{i}',\,y_{i}',$ on n’altère pas la forme canonique des équations.

Nous supposerons que $n_{2}$ ne s’annule pas quand $x_{1}$ reste inférieur à une certaine limite $a.$ Alors ${\frac {dy_{2}}{dt}}$ conservera toujours le même signe et l’on aura, par exemple,

${\frac {dy_{2}}{dt}}>0.$

Cette inégalité, vraie pour $\mu =0,$ le sera encore pour les petites valeurs de $\mu .$

Alors les relations

${\begin{aligned}y_{2}&=0,&|x_{1}|&<a-\varepsilon \end{aligned}}$

définiront un certain domaine plan $\mathrm {D}$ qui aura d’ailleurs la forme d’un cercle.

Les trajectoires issues d’un point de ce domaine ne seront alors jamais tangentes à un plan passant par l’axe des $z,$ du moins avant d’avoir recoupé de nouveau le demi-plan $y_{2}=0.$ Notre domaine pourra donc jouer le rôle du domaine $\mathrm {D}$ du n^o 310.

Les équations (1) admettent l’invariant intégral

$\int dx_{1}\,dx_{2}\,dy_{1}\,dy_{2},$

d’où l’on déduit le suivant à l’aide de l’intégrale $\mathrm {F} =\mathrm {const.}$

$\mathrm {J} =-\int {\frac {dx_{1}\,dy_{1}\,dy_{2}}{\dfrac {d\mathrm {F} }{dx_{2}}}}\cdot$

Mais ${\frac {d\mathrm {F} }{dx_{2}}}$ est égal à $-{\frac {dy_{2}}{dt}}$ et par conséquent négatif. L’invariant $\mathrm {J}$ est alors un invariant positif.

Les résultats des n^os 306 et 308 sont donc applicables aux courbes tracées dans le domaine $\mathrm {D} .$

Cela posé, soit $b$ une valeur de $x_{1}$ plus petite que $a-\varepsilon$ et telle que les valeurs correspondantes de $n_{1}$ et de $n_{2}$ satisfassent à la relation

$m_{1}n_{1}+m_{2}n_{2}=0,$

où $m_{1}$ et $m_{2}$ sont deux entiers premiers entre eux.

La courbe

$x_{1}=b,$

qui est une circonférence, sera une courbe invariante pour $\mu =0.$

En supposant toujours $\mu =0,$ les trajectoires issues des divers points de cette circonférence auront pour équation générale

${\begin{aligned}y_{1}&=n_{1}t+\mathrm {const.} ,&y_{2}&=n_{2}t+\mathrm {const.} ,\end{aligned}}$

d’où

$y_{1}={\frac {n_{1}}{n_{2}}}y_{2}+\mathrm {const.}$

Pour avoir les conséquents successifs d’un point donné, il suffira de faire successivement

$y_{2}=0,\quad y_{2}=2\pi ,\quad y_{2}=4\pi ,\quad \ldots ,\quad y_{2}=2k\pi .$

Pour passer d’un point à son conséquent il suffit donc d’augmenter $y_{1}$ de

${\frac {2\pi n_{1}}{n_{2}}}=-{\frac {2\pi m_{2}}{m_{1}}},$

d’où il suit que tous les points de la circonférence invariante $x_{1}=b$ coïncideront avec leur $m_{1}\!\!$^ième conséquent.

Ce point et ses $m_{1}-1$ premiers conséquents sont distribués sur cette circonférence dans un ordre circulaire qu’il est aisé de retrouver quand on connaît les deux entiers $m_{1}$ et $m_{2}\,;$ je l’appellerai l’ordre $\Omega .$

Ne supposons plus $\mu =0\,;$ les équations (1), d’après le Chapitre III, admettront encore des solutions périodiques peu différentes des solutions

${\begin{aligned}x_{1}&=b,&y_{1}&=n_{1}t+\mathrm {const.} ,&y_{2}&=n_{2}t+\mathrm {const.} \end{aligned}}$

Elles en admettront au moins deux dont l’une instable et l’autre stable. À chacune de ces solutions périodiques correspondra une trajectoire fermée ; je considère une de ces trajectoires que j’appelle $\mathrm {T}$ et qui correspondra à une solution instable, afin que par $\mathrm {T}$ passent deux surfaces asymptotiques.

Soit $\mathrm {M} _{0}$ le point où cette trajectoire perce le demi-plan $y_{2}=0,$ $\mathrm {M} _{1},$ $\mathrm {M} _{2},\,\ldots$ ses conséquents successifs (fig. 7). Le point $M_{0}$ coïncidera avec son $m_{1}\!\!$^ième conséquent $\mathrm {M} _{m}.$

Je joins le point $\mathrm {M} _{k}$ au centre de la circonférence $x_{1}=b\,;$ le rayon ainsi mené coupera la circonférence en un point $\mathrm {M} _{k}'$ très voisin de $\mathrm {M} _{k}.$ Les divers points $\mathrm {M} _{k}'$ se succéderont sur la circonférence dans l’ordre circulaire $\Omega .$

J’ai fait la figure en supposant, pour fixer les idées, $m_{1}=5,$ $m_{2}=2.$ La trajectoire fermée $\mathrm {T}$ coupe le demi-plan aux cinq points $\mathrm {M} _{0},$ $\mathrm {M} _{1},$ $\mathrm {M} _{2},$ $\mathrm {M} _{3},$ $\mathrm {M} _{4}.$ Par cette trajectoire passent deux surfaces asymptotiques qui se coupent.

L’intersection de ces surfaces asymptotiques avec le demi-plan se composera de diverses courbes ; nous aurons deux courbes se coupant en $\mathrm {M} _{0},$ deux en $\mathrm {M} _{1},$ deux en $\mathrm {M} _{2},$ deux en $\mathrm {M} _{3},$ deux en $\mathrm {M} _{4}.$ Toutes ces courbes sont représentées sur la figure.

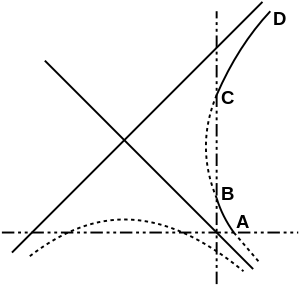
Fig. 7.

Considérons en particulier les deux courbes qui passent en $\mathrm {M} _{0}\,;$ nous distinguerons quatre branches de courbe, à savoir $\mathrm {M} _{0}\mathrm {A} _{0},$ $\mathrm {M} _{0}\mathrm {B} _{2},$ $\mathrm {M} _{0}\mathrm {P} _{0},$ $\mathrm {M} _{0}\mathrm {Q} _{0}\,;$ les deux premières sont représentées en trait plein, les deux dernières en trait pointillé ; la première et la troisième, comme la deuxième et la quatrième sont dans le prolongement l’une de l’autre.

De même à chacun des points $\mathrm {M}$ aboutiront quatre branches de courbe dont deux sont représentées en trait plein et deux en trait pointillé et qui sont deux à deux dans le prolongement l’une de l’autre.

Soit $\mathrm {A} _{0}$ un point de la branche $\mathrm {M} _{0}\mathrm {B} _{0}\,;$ par $\mathrm {A} _{0}$ menons un rayon allant au centre de la circonférence $x_{1}=b$ et prolongeons ce rayon jusqu’en $\mathrm {B} _{0}$ à sa rencontre avec la courbe en trait plein $\mathrm {M} _{3}\mathrm {B} _{0}.$ Comme $\mu$ est très petit et que toutes nos courbes diffèrent très peu de la circonférence $x_{1}=b,$ le segment $\mathrm {A} _{0}\mathrm {B} _{0}$ sera très petit.

Nous voyons alors que $\mathrm {M} _{1}\mathrm {A} _{1},$ $\mathrm {M} _{2}\mathrm {A} _{2},$ $\mathrm {M} _{3}\mathrm {A} _{3},$ $\mathrm {M} _{4}\mathrm {A} _{4},$ $\mathrm {M} _{0}\mathrm {A} _{5}$ sont les conséquents successifs de $\mathrm {M} _{0}\mathrm {A} _{0}\,;$ que $\mathrm {M} _{4}\mathrm {B} _{1}$ $\mathrm {M} _{0}\mathrm {B} _{2},$ $\mathrm {M} _{1}\mathrm {B} _{3},$ $\mathrm {M} _{2}\mathrm {B} _{4},$ $\mathrm {M} _{4}\mathrm {B} _{5}$ sont ceux de $\mathrm {M} _{3}\mathrm {B} _{0}$ et enfin que $\mathrm {A} _{1}\mathrm {B} _{1},$ $\mathrm {A} _{2}\mathrm {B} _{2},\,\ldots ,$ $\mathrm {A} _{5}\mathrm {B} _{5}$ sont ceux de $\mathrm {A} _{0}\mathrm {B} _{0}.$

Les arcs $\mathrm {A} _{1}\mathrm {B} _{1},$ $\mathrm {A} _{2}\mathrm {B} _{2},\,\ldots ,$ $\mathrm {A} _{5}\mathrm {B} _{5}$ ne sont plus rectilignes en général, mais sont des arcs de courbe très petits.

La partie de la figure en trait plein reproduit alors les fig. 1 ou 2 du n^o 308 ; et l’ensemble de nos courbes en trait plein représente une courbe invariante $\mathrm {K} .$

J’ai fait la figure dans la première hypothèse qui, comme nous l’avons vu, doit être rejetée ainsi que la cinquième ; d’après ce que j’ai dit au n^o 309, il en est de même de la deuxième.

Il faut examiner la quatrième avec plus de détail. Pour cela, cherchons l’équation de nos surfaces asymptotiques. D’après ce que nous avons vu au n^o 207, cette équation peut s’obtenir de la façon suivante :

On forme une fonction $\mathrm {S}$ qui est développable suivant les puissances de ${\sqrt {\overset {}{\mu }}},$ de telle sorte que

$\mathrm {S} =\mathrm {S} _{0}+{\sqrt {\overset {}{\mu }}}\,\mathrm {S} _{1}+\ldots +\mu ^{\frac {p}{2}}\mathrm {S} _{p}+\ldots .$

Quant à $\mathrm {S} _{p},$ c’est une fonction périodique de période $2\pi$ par rapport à $y_{2}'$ et $4\pi$ par rapport à $y_{1}'.$

Nous aurons ensuite

${\begin{aligned}x_{1}'&={\frac {d\mathrm {S} }{dy_{1}'}},&x_{2}'&={\frac {d\mathrm {S} }{dy_{2}'}},\\\end{aligned}}$

(4)

$x_{1}=m_{1}\,{\frac {d\mathrm {S} }{dy_{1}'}}+m_{2}\,{\frac {d\mathrm {S} }{dy_{2}'}}\cdot$

L’équation (4) est l’équation de la surface asymptotique.

Si la série $\mathrm {S}$ était convergente, la périodicité des $\mathrm {S} _{p}$ entraînerait cette conséquence que nos courbes devraient être fermées et que les deux points $\mathrm {A} _{0}$ et $\mathrm {B} _{0}$ coïncideraient. Mais il n’en est pas ainsi (cf. n^o 225, et sqq.).

Que signifie alors l’équation (4) ? Elle ne peut être vraie qu’au point de vue formel ; c’est-à-dire que si $\Sigma _{p}$ est la somme des $p+1$ premiers termes de la série $\mathrm {S}$ de telle façon que

$\Sigma _{p}=\mathrm {S} _{0}+{\sqrt {\overset {}{\mu }}}\,\mathrm {S} _{1}+\ldots +\mu ^{\frac {p}{2}}\mathrm {S} _{p},$

l’équation

(4 bis)

$x_{1}=m_{1}\,{\frac {d\Sigma _{p}}{dy_{1}'}}+m_{2}\,{\frac {d\Sigma _{p}}{dy_{2}'}}$

sera vraie aux quantités près de l’ordre $\mu ^{\frac {p+1}{2}}.$

Mais l’équation (4 bis) représente une surface fermée et $p$ est aussi grand que l’on veut.

Nous devons donc conclure que la distance $\mathrm {A} _{0}\mathrm {B} _{0}$ est un infiniment petit d’ordre infini (cf. n^os 225 et suivants). D’autre part, la distance $\mathrm {A} _{0}\mathrm {A} _{5}$ (ou $\mathrm {B} _{0}\mathrm {B} _{5}$) est de l’ordre de ${\sqrt {\overset {}{\mu }}}$ et est par conséquent infiniment petit d’ordre ${\tfrac {1}{2}}\cdot$

La distance $\mathrm {A} _{0}\mathrm {B} _{0}$ est donc infiniment petite par rapport à $\mathrm {A} _{0}\mathrm {A} _{1},$ ce qui montre que la quatrième hypothèse doit être rejetée.

La seule hypothèse possible est donc la troisième.

Donc les deux arcs $\mathrm {A} _{0}\mathrm {A} _{5}$ et $\mathrm {B} _{0}\mathrm {B} _{5}$ se coupent.

Application au problème restreint.

313.Je vais appliquer les principes précédents au problème du n^o 9 et j’adopterai les notations de ce numéro ; nous aurons par conséquent les équations canoniques

${\begin{aligned}{\frac {dx_{i}'}{dt}}&={\frac {d\mathrm {F} '}{dy_{i}'}},&{\frac {dy_{i}'}{dt}}&=-{\frac {d\mathrm {F} '}{dx_{i}'}},\end{aligned}}$

où l’on a posé

(5)

$\left\{{\begin{aligned}x_{1}'&=\mathrm {L} ,&x_{2}'&=\mathrm {G} ,\\y_{1}'&=l,&y_{2}'&=g-t,\\\end{aligned}}\right.$

et, d’autre part,

${\begin{aligned}\mathrm {F} '&=\mathrm {R} +\mathrm {G} =\mathrm {F} _{0}+\mu \,\mathrm {F} _{1}+\ldots ,\\\mathrm {F} _{0}&={\frac {1}{{2}x_{1}'^{2}}}+x_{2}'.\end{aligned}}$

Posons maintenant

${\begin{aligned}x_{1}&=\mathrm {L} -\mathrm {G} ,&x_{2}&=\mathrm {L} +\mathrm {G} ,\\2y_{1}&=l-g+t,&2y_{2}&=l+g-t\,;\end{aligned}}$

les équations conserveront la forme canonique et deviendront

${\begin{aligned}{\frac {dx_{i}'}{dt}}&={\frac {d\mathrm {F} '}{dy_{i}}},&{\frac {dy_{i}'}{dt}}&=-{\frac {d\mathrm {F} '}{dx_{i}}}\,;\end{aligned}}$

on aura d’ailleurs

$\mathrm {F} _{0}={\frac {2}{(x_{1}+x_{2})^{2}}}+{\frac {x_{2}-x_{1}}{2}},$

d’où

${\begin{aligned}n_{1}&={\frac {+4}{(x_{1}+x_{2})^{3}}}+{\frac {1}{2}},&n_{2}&={\frac {+4}{(x_{1}+x_{2})^{3}}}-{\frac {1}{2}}\cdot \end{aligned}}$

Si nous supposons l’excentricité très petite, $\mathrm {L}$ et $\mathrm {G}$ différeront très peu en valeur absolue ; donc L’une des deux quantités $x_{1}$ et $x_{2}$ est très petite.

J’observe de plus que les égalités

$\mathrm {L} ={\sqrt {\overset {}{a}}},\qquad \mathrm {G} ={\sqrt {a(1-e^{2})}}$

montrent que $\mathrm {G}$ est toujours plus petit que $\mathrm {L}$ en valeur absolue. Donc $x_{1}$ et $x_{2}$ sont essentiellement positifs.

Supposons $x_{1}$ très petit, la fonction $\mathrm {F} '$ sera une fonction de $a$ et de $l+g-t$ développable en outre suivant les puissances de $e\cos {}g$ et de $e\sin {}g.$ Ce sera donc aussi une fonction de $x_{2}$ et de $y_{2}$ développable en outre suivant les puissances de

${\sqrt {{\overset {}{x}}_{1}}}\cos y_{1}$ et ${\sqrt {{\overset {}{x}}_{1}}}\sin y_{1}.$

Elle sera périodique de période $2\pi$ tant en $y_{1}$ qu’en $y_{2}.$

Si, au contraire, c’est $x_{2}$ qui est très petit, la fonction $\mathrm {F} '$ sera une fonction de $x_{1}$ et de $y_{1},$ développable en outre suivant les puissances de

${\sqrt {{\overset {}{x}}_{2}}}\cos y_{2}$ et ${\sqrt {{\overset {}{x}}_{2}}}\sin y_{2}.$

Mais nous supposons nos quatre variables $x$ et $y$ liées par l’équation des forces vives

$\mathrm {F} =\mathrm {C} \,;$

cette équation se réduit approximativement à

$\mathrm {F} _{0}=\mathrm {C} .$

Construisons la courbe $\mathrm {F} _{0}=\mathrm {C}$ en prenant $x_{1}$ et $x_{2}$ comme les coordonnées d’un point dans un plan.

L’équation peut s’écrire

$(x_{1}+x_{2})^{2}(2\mathrm {C} +x_{1}-x_{2})=4.$

Cette courbe a deux asymptotes

${\begin{aligned}x_{1}+x_{2}&=0,&x_{2}-x_{1}&=2\mathrm {C} \end{aligned}}$

et elle est symétrique par rapport à la première de ces deux asymptotes.

Mais il importe de remarquer que la seule partie de la courbe qui nous soit utile est celle qui est située dans le premier quadrant

$x_{1}>0,\quad x_{2}>0.$

Suivant les valeurs de $\mathrm {C} ,$ la courbe peut présenter une des formes représentées par les deux figures suivantes :

Fig. 8.

Les axes de coordonnées sont représentés en trait mixte, les asymptotes et les parties utiles de la courbe en trait plein, les parties inutiles de la courbe en trait pointillé.

Nous supposerons que l’on donne à $\mathrm {C}$ une valeur telle que la courbe présente la forme de la fig. 9 et qu’elle comprenne deux arcs utiles $\mathrm {AB}$ et $\mathrm {CD} .$ Nous n’envisagerons d’ailleurs que l’arc $\mathrm {AB} .$

Remarquons que quand on parcourt cet arc $\mathrm {AB} ,$ $x_{1}$ décroît constamment de $\mathrm {OA}$ à zéro, $x_{2}$ croît constamment de zéro à $\mathrm {OB}$ et ${\frac {x_{2}}{x_{1}}}$ croît constamment de zéro à $+\infty .$

Si nous construisons maintenant la courbe $\mathrm {F} =\mathrm {C}$ en regardant $y_{1}$ et $y_{2}$ comme des constantes et $x_{1}$ et $x_{2}$ comme les coordonnées d’un point dans un plan, la courbe différera peu de $\mathrm {F} _{0}=\mathrm {C}$ et pourra encore être représentée par la fig. 9 ; elle aura un arc utile $\mathrm {AB}$ et quand on parcourra cet arc le rapport ${\frac {x_{2}}{x_{1}}}$ croîtra constamment de zéro à $+\infty .$

Fig. 9.

On est ainsi conduit au mode de représentation géométrique suivant : on représentera la situation du système par le point dont les coordonnées rectangulaires sont

${\begin{array}{c}{\dfrac {{\sqrt {{\overset {}{x}}_{2}}}\cos y_{2}}{{\sqrt {{\overset {}{x}}_{2}+4x_{1}}}-2{\sqrt {{\overset {}{x}}_{1}}}\cos y_{1}}},\quad {\dfrac {{\sqrt {{\overset {}{x}}_{2}}}\sin y_{2}}{{\sqrt {{\overset {}{x}}_{2}+4x_{1}}}-2{\sqrt {{\overset {}{x}}_{1}}}\cos y_{1}}},\\[0.75ex]{\dfrac {2{\sqrt {{\overset {}{x}}_{1}}}\sin y_{1}}{{\sqrt {{\overset {}{x}}_{2}+4x_{1}}}-2{\sqrt {{\overset {}{x}}_{1}}}\cos y_{1}}}\cdot \end{array}}$

Ces trois fonctions sont développables suivant les puissances de ${\sqrt {{\overset {}{x}}_{1}}}\cos {y_{1}}$ et ${\sqrt {{\overset {}{x}}_{1}}}\sin {y_{1}},$ si $x_{1}$ est très petit, et suivant celles de ${\sqrt {{\overset {}{x}}_{2}}}\cos {y_{2}}$ et ${\sqrt {{\overset {}{x}}_{2}}}\sin {y_{2}},$ si $x_{2}$ est très petit. Elles ne dépendent que du rapport ${\frac {x_{1}}{x_{2}}}.$

À chaque système de valeurs de $y_{1}$ et de $y_{2}$ et à chaque point de l’arc utile $\mathrm {AB}$ correspond ainsi un point de l’espace et un seul.

Le déterminant fonctionnel des trois coordonnées par rapport à $y_{1},\,y_{2}$ et au rapport ${\sqrt {\frac {{\overset {}{x}}_{1}}{x_{2}}}}$ conserve toujours le même signe.

Nous pouvons donc appliquer les résultats du numéro précédent à l’intérieur de tout domaine $\mathrm {D}$ où $n_{2}$ ne s’annule pas.

Or $n_{2}$ s’annule pour $x_{1}+x_{2}=2.$

Mais si l’on a $x_{1}+x_{2}=2,$ $x_{1}>0,$ $x_{2}>0,$ on aura évidemment

${\frac {2}{(x_{1}+x_{2})^{2}}}+{\frac {x_{2}-x_{1}}{2}}<{\frac {2}{(x_{1}+x_{2})^{2}}}+{\frac {x_{2}+x_{1}}{2}}={\frac {3}{2}}\cdot$

Or, le premier membre de cette égalité est $\mathrm {F} _{0},$ et en construisant la courbe $\mathrm {F} _{0}=\mathrm {C} ,$ nous avons supposé que nous nous trouvions dans le cas de la fig. 9 ; or le cas de la fig. 9 suppose

$\mathrm {C} >{\frac {3}{2}}\cdot$

Comme $\mathrm {F} _{0}$ diffère très peu de $\mathrm {F}$ et par conséquent de $\mathrm {C} ,$ nous ne pourrons avoir à la fois

$\mathrm {C} >{\frac {3}{2}},\quad \mathrm {F} _{0}<{\frac {3}{2}}$

(à moins que $\mathrm {C}$ ne soit très voisin de sa limite ${\tfrac {3}{2}}$, ce que nous ne supposerons pas).

On n’aura donc pas, dans les conditions où nous nous sommes placés, $n_{2}=0.$

Ainsi les résultats du numéro précédent sont applicables et si l’on construit les surfaces asymptotiques et que l’on envisage l’intersection de ces surfaces avec le demi-plan $y_{2}=0,$ les deux arcs analogues à ceux que nous avons appelés plus haut $\mathrm {A} _{0}\mathrm {A} _{5}$ et $\mathrm {B} _{0}\mathrm {B} _{5}$ se couperont.

J’ajouterai encore un mot :

Les coordonnées du troisième corps par rapport au grand et au petit axe de l’ellipse qu’il décrit sont, d’après une formule bien connue,

${\begin{alignedat}{3}\mathrm {L} ^{2}&(\cos l&{}+{}&\ldots ),\\\mathrm {LG} &(\sin l&{}+{}&\ldots ),\end{alignedat}}$

On voit ainsi que, quand $\mathrm {G}$ change de signe, la seconde de ces coordonnées change de signe.

Il en résulte que la planète troublée circule dans le même sens que la planète troublante si $\mathrm {G}$ est positif et en sens contraire si $\mathrm {G}$ est négatif.