Théorie mathématique de la lumière/2/Chap.09

Henri Poincaré

Théorie mathématique de la lumière

Georges Carré, 1892 (2, p. 199-226).

CHAPITRE IX

DIFFRACTION DES ONDES CONVERGENTES

123. Ondes cylindriques. — Soit une onde cylindrique, ayant pour axe $\mathrm {O} x\,;$ si les vibrations sont parallèles à $\mathrm {O} x,$

$\eta =\zeta =0$

et la condition de transversalité devient

$\theta ={\frac {d\xi }{dx}}=0.$

$\xi$ ne dépend donc que de $y,\,z,\,t.$

Posons

${\begin{aligned}y&=\rho \cos \omega \\z&=\rho \sin \omega .\\\end{aligned}}$

$\xi$ deviendra une fonction de $\rho ,\,\omega ,\,t.$

L’équation

(1)

$\Delta \xi +\alpha ^{2}\xi =0,$

à laquelle doit satisfaire $\xi ,$ prend en fonction de $\rho ,\,\omega ,$ la forme :

(2)

${\frac {d^{2}\xi }{d\rho ^{2}}}+{\frac {1}{\rho }}\,{\frac {d\xi }{d\rho }}+{\frac {1}{\rho ^{2}}}\,{\frac {d^{2}\xi }{d\omega ^{2}}}+\alpha ^{2}\xi =0.$

$\xi$ est une fonction périodique de $\omega$ et peut être développé suivant la formule de Fourier :

${\begin{alignedat}{6}\xi =\lambda _{0}&+\lambda _{1}\cos \omega &&+\lambda _{2}\cos 2\omega &&+\cdots +\lambda _{n}\cos n\omega \\&+\mu _{1}\sin \omega &&+\mu _{2}\sin 2\omega &&+\cdots +\mu _{n}\sin n\omega ,\\\end{alignedat}}$

$\lambda _{0},\,\lambda _{1}\,\dots \,\lambda _{n},\,\mu _{0},\,\mu _{1}\,\dots \,\mu _{n}$ étant des fonctions de $\rho .$

Substituons à $\xi$ cette valeur dans (2).

$\xi =\sum \lambda _{n}\cos n\omega +\sum \mu _{n}\sin n\omega$

${\frac {d^{2}\xi }{d\omega ^{2}}}=\sum -n^{2}\lambda _{n}\cos n\omega +\sum -n^{2}\mu _{n}\sin n\omega .$

Le premier membre de (2) doit être identiquement nul : les coefficients de $\cos n\omega$ et de $\sin n\omega$ doivent être nuls identiquement :

$\lambda _{n}$ satisfait donc à l’équation différentielle :

(3)

${\frac {d^{2}\lambda _{n}}{d\rho ^{2}}}+{\frac {1}{\rho }}\,{\frac {d\lambda _{n}}{d\rho }}-{\frac {n^{2}}{\rho ^{2}}}\,\lambda _{n}+\alpha ^{2}\lambda _{n}=0.$

Faisons $\;\alpha =1\qquad \lambda _{n}=u.$

(4)

${\frac {d^{2}u}{d\rho ^{2}}}+{\frac {1}{\rho }}\,{\frac {du}{d\rho }}+u\left(1-{\frac {n^{2}}{\rho ^{2}}}\right)=0.$

$\lambda _{n}$ doit rester fini pour $\rho =0.$ Les seules solutions de l’équation (4) qui restent finies pour $\rho =0$ sont de la forme

$u=\mathrm {A} \mathrm {J} _{n}(\rho ),$

$\mathrm {A}$ étant une constante et $\mathrm {J} _{n}(\rho )$la fonction de Bessel :

$\mathrm {J} _{n}(\rho )={\frac {\left({\dfrac {\rho }{2}}\right)^{n}}{n!}}\left[1-{\frac {\left({\dfrac {\rho }{2}}\right)^{2}}{1.(n+1)}}+{\frac {\left({\dfrac {\rho }{2}}\right)^{4}}{1.2..(n+1)(n+2)}}-{\frac {\left({\dfrac {\rho }{2}}\right)^{6}}{1.2.3.(n+1)(n+2)(n+3)}}\cdots \right]$

Pour avoir $\lambda _{n}$ il suffit de changer $\rho$ en $\alpha \rho \,:$

$\lambda _{n}=\mathrm {A} _{n}\mathrm {J} _{n}(\alpha \rho ).$

De même :

$\mu _{n}=\mathrm {B} _{n}\mathrm {J} _{n}(\alpha \rho ).$

Substituons ces valeurs de $\lambda _{n}$ et de $\mu _{n}$ dans $\xi ,$ il vient ;

${\begin{aligned}\xi &=\mathrm {A} _{0}\mathrm {J} _{0}(\alpha \rho )+\mathrm {J} _{1}(\alpha \rho )\left(\mathrm {A} _{1}\cos \omega +\mathrm {B} _{1}\sin \omega \right)\\&+\mathrm {J} _{2}(\alpha \rho )\left(\mathrm {A} _{2}\cos {2\omega }+\mathrm {B} _{2}\sin {2\omega }\right)+\!\cdots \!+\mathrm {J} _{n}(\alpha \rho )\left(\mathrm {A} _{n}\cos {n\omega }+\mathrm {B} _{n}\sin {n\omega }\right)\\\end{aligned}}$

124. Nous allons appliquer cette formule à l’étude des phénomènes qui se passent au voisinage d’une ligne focale.

Fig. 29.

Soient un miroir en forme de cylindre parabolique (fig. 29), $\mathrm {ASB}$ la parabole de base ; nous supposerons que les extrémités $\mathrm {A}$ et $\mathrm {B}$ sont également distantes de $\mathrm {S} \,:$ le plan mené par l’axe $\mathrm {SF}$ de la parabole parallèlement aux génératrices du cylindre sera un plan de symétrie.

Une onde plane tombe sur ce cylindre : les plans d’onde sont perpendiculaires à l’axe $\mathrm {SF} .$ D’après la théorie géométrique de la réflexion, les rayons réfléchis passent par le foyer $\mathrm {F}$ et les ondes réfléchies passent par la ligne focale, menée en $\mathrm {F}$ parallèlement aux génératrices du cylindre. Les rayons formeraient donc un faisceau limité par les plans parallèles aux génératrices, dont les traces sur le plan de la figure sont $\mathrm {AFA'}$ et $\mathrm {BFB'} .$

Prenons la ligne focale comme axe des $x\,;$ comme plan des $xy$ le plan contenant cet axe et l’axe $\mathrm {SF}$ de la parabole : ce sera le plan de symétrie. Posons ensuite :

${\begin{aligned}y&=\rho \cos \omega \\z&=\rho \sin \omega .\\\end{aligned}}$

Supposons que la vibration soit parallèle à $\mathrm {O} x\,;$ nous pourrons écrire :

$\xi =f(\rho ,\omega )\cos pt+f_{1}(\rho ,\omega )\sin pt,$

$\xi$ doit vérifier l’équation

$\Delta \xi +\alpha ^{2}\xi =0.$

Nous avons trouvé que $\xi$ devait alors être de la forme^[1] :

${\begin{alignedat}{6}\xi =\mathrm {A} _{0}\mathrm {J} _{0}(\alpha \rho )&+\mathrm {A} _{1}\mathrm {J} _{1}(\alpha \rho )\cos \omega &&+\mathrm {A} _{2}\mathrm {J} _{2}(\alpha \rho )\cos 2\omega &&+\cdots \\&+\mathrm {B} _{1}\mathrm {J} _{1}(\alpha \rho )\sin \omega &&+\mathrm {B} _{2}\mathrm {J} _{2}(\alpha \rho )\sin 2\omega &&+\cdots \\\end{alignedat}}$

$\mathrm {A_{0},\,A_{1},\,\dots ,\,B_{0},\,B_{1},\,\dots }$ ne dépendent pas de $\rho$ et de $\omega ,$ mais sont fonctions de $t.$

${\begin{aligned}\mathrm {A} _{n}&=\mathrm {A} '_{n}\cos pt+\mathrm {A} ''_{n}\sin pt\\\mathrm {B} _{n}&=\mathrm {B} '_{n}\cos pt+\mathrm {B} ''_{n}\sin pt.\\\end{aligned}}$

Le plan des $xy$ étant un plan de symétrie, $\xi$ ne change pas quand on remplace $\omega$ par $-\omega ,$ les termes qui contiennent les sinus doivent donc être nuls, et l’expression de $\xi$ se réduire à :

${\begin{aligned}\xi &=\sum \mathrm {A} _{n}\mathrm {J} _{n}(\alpha \rho )\cos n\omega \\[1ex]&=\sum \mathrm {A} _{2n}\mathrm {J} _{2n}(\alpha \rho )\cos 2n\omega +\sum \mathrm {A} _{2n+1}\mathrm {J} _{2n+1}(\alpha \rho )\cos(2n+1)\omega .\\\end{aligned}}$

Si $\rho$ devient très grand, nous pourrons calculer une valeur asymptotique de $\xi .$ Nous avons donné déjà (85) une formule asymptotique pour $\mathrm {J} _{0}(\rho )\,:$

$\mathrm {J} _{0}(\rho )={\sqrt {\frac {2}{\pi \rho }}}\,\cos \left(\rho -{\frac {\pi }{4}}\right)\cdot$

D’autre part, les fonctions $\mathrm {J}$ sont liées par la relation de récurrence :

$n\mathrm {J} _{n}(\rho )={\frac {\rho }{2}}\left[\mathrm {J} _{n-1}(\rho )+\mathrm {J} _{n+1}(\rho )\right]$

ou

$\mathrm {J} _{n-1}(\rho )+\mathrm {J} _{n+1}(\rho )={\frac {2n}{\rho }}\,\mathrm {J} _{n}(\rho )$

quand $\rho$ devient très grand, le second membre tend vers $0$ et approximativement :

$\mathrm {J} _{n-1}(\rho )+\mathrm {J} _{n+1}(\rho )=0$

d’où :

${\begin{aligned}\mathrm {J} _{2n}(\rho )&=(-1)^{n}\mathrm {J} _{0}\\\mathrm {J} _{2n+1}(\rho )&=(-1)^{n}\mathrm {J} _{1}.\\\end{aligned}}$

Pour calculer $\mathrm {J} _{1},$ nous ferons usage de la relation

${\frac {d\mathrm {J} _{1}}{d\rho }}=\mathrm {J} _{0}(\rho ),$

d’où nous tirerons :

$\mathrm {J} _{1}={\sqrt {\frac {2}{\pi \rho }}}\,\sin \left(\rho -{\frac {\pi }{4}}\right)\cdot$

En effet différencions :

${\frac {d\mathrm {J} _{1}}{d\rho }}={\sqrt {\frac {2}{\pi \rho }}}\,\cos \left(\rho -{\frac {\pi }{4}}\right)-{\frac {1}{\rho }}{\sqrt {\frac {1}{2\pi \rho }}}\,\sin \left(\rho -{\frac {\pi }{4}}\right)$.

Le second terme contenant $\rho$ en dénominateur est négligeable, et il reste

${\frac {d\mathrm {J} _{1}}{d\rho }}={\sqrt {\frac {2}{\pi \rho }}}\,\cos \left(\rho -{\frac {\pi }{4}}\right)=\mathrm {J} _{0}(\rho ).$

D’une manière générale, nous aurons quel que soit $n\,:$

$\mathrm {J} _{n}(\rho )={\sqrt {\frac {2}{\pi \rho }}}\,\cos \left(\rho -{\frac {\pi }{4}}-n\,{\frac {\pi }{2}}\right)\cdot$

Posons pour abréger :

$\mathrm {H} ={\sqrt {\frac {2}{\pi \alpha \rho }}}\quad$ et $\quad \alpha \rho -{\frac {\pi }{4}}=\psi$

$\mathrm {J} _{n}(\alpha \rho )=\mathrm {H} \cos \left(\psi -n\,{\frac {\pi }{2}}\right)$

et pour $\rho$ très grand, nous aurons :

${\begin{aligned}\xi &=\sum \mathrm {H} \mathrm {A} _{2n}(-1)^{n}\cos \psi \cos 2n\omega \\[0.75ex]&+\sum \mathrm {H} \mathrm {A} _{2n+1}(-1)^{n}\sin \psi \cos(2n+1)\omega ,\\\end{aligned}}$

ce que j’écrirai :

(1)

$\xi =\mathrm {HB} \cos \psi +\mathrm {HC} \sin \psi$

avec

${\begin{aligned}\mathrm {B} &=\sum \mathrm {A} _{2n}(-1)^{n}\cos 2n\omega \\[1ex]\mathrm {C} &=\sum \mathrm {A} _{2n+1}(-1)^{n}\cos(2n+1)\omega .\\\end{aligned}}$

Remarquons que les coefficients $\mathrm {A} _{n}$ et par conséquent $\mathrm {B}$ et $\mathrm {C}$ dépendent du temps. $\mathrm {B}$ ne contient que des multiples pairs de $\omega$ et ne change pas quand on remplace $\omega$ par $\pi -\omega .$

Au contraire $\mathrm {C} ,$ qui ne renferme que des multiples impairs de $\omega ,$ change de signe quand $\omega$ se change en $\pi -\omega .$

125. Cette expression donne la valeur de $\xi$ quand on s’écarte beaucoup du foyer. Mais à une grande distance du foyer, il n’y aura pas de diffraction sensible ; nous pourrons donc admettre que l’amplitude qui est en raison inverse de ${\sqrt {\rho }},$ est égale à $\mathrm {H}$ à l’intérieur du faisceau et à $0$ à l’extérieur. Il convient d’observer de plus que l’onde est convergente en-deçà du foyer et divergente au-delà.

Soit $\beta$ la demi-ouverture $\mathrm {SFA}$ du miroir.

Pour les valeurs de $\omega$ comprises entre $0$ et $+\beta ,$ l’onde est convergente, d’où :

$\xi =\mathrm {H} \cos \left(\alpha \rho -{\frac {\pi }{4}}+pt\right)=\mathrm {H} \cos(\psi +pt)$

Pour $\omega$ compris entre $+\beta$ et $\pi -\beta ,$ on est en dehors du faisceau et il n’y a pas de lumière :

$\xi =0.$

Pour $\omega$ compris entre $\pi -\beta$ et $\pi ,$ l’onde est divergente et l’on a :

$\xi =\mathrm {H} \cos(\psi -pt)$

En comparant cette expression de $\xi$ à l’expression (1) et identifiant les coefficients de $\cos \psi$ et de $\sin \psi ,$ nous trouverons :

${\begin{aligned}0<\omega <\beta \;\;&\left\{{\begin{aligned}\mathrm {B} &=\cos pt\\[0.75ex]\mathrm {C} &=\sin pt\\\end{aligned}}\right.\\[0.75ex]\beta <\omega <\pi -\beta \;\;&\left\{{\begin{aligned}\mathrm {B} &=0\\[0.75ex]\mathrm {C} &=0\\\end{aligned}}\right.\\[0.75ex]\pi -\beta <\omega <\pi \;\;&\left\{{\begin{aligned}\mathrm {B} &=\cos pt\\[0.75ex]\mathrm {C} &=\sin pt\\\end{aligned}}\right.\\\end{aligned}}$

Ces fonctions $\mathrm {B}$ et $\mathrm {C}$ sont donc définies entre $0$ et $\pi$ et par conséquent entre $-\pi$ et $+\pi .$ Il suffit pour étendre la définition à ce second intervalle de changer $\omega$ en $\pi -\omega ,$ ce qui modifie le signe de $\mathrm {C}$ sans changer celui de $\mathrm {B} .$

La formule de Fourier permet alors de calculer les coefficients $\mathrm {A} \,;$ on trouve :

${\begin{aligned}\mathrm {A} _{2n}&=(-1)^{n}\,{\frac {\sin 2n\beta }{2n}}\,{\frac {4}{\pi }}\\[0.75ex]\mathrm {A} _{2n+1}&=(-1)^{n}\,{\frac {\sin(2n+1)\beta }{2n}}\,{\frac {4}{\pi }}\\\end{aligned}}$

126. Revenons à présent à la valeur exacte de $\xi \,:$ dans le plan des $xz,$ qui est le plan mené par la ligne focale perpendiculairement à l’axe $\mathrm {SF} ,$ l’expression asymptotique de $\xi$ serait nulle.

Pour ce plan focal, $\omega ={\frac {\pi }{2}}$ et par suite :

${\begin{aligned}\cos(2n+1)\omega &=0\\\cos 2n\omega &=(-1)^{n}\\\end{aligned}}$

Donc :

$\xi =\sum \mathrm {A} _{2n}(-1)^{n}\mathrm {J} _{2n}(\alpha \rho ).$

Pour achever le calcul nous allons nous servir de l’expression de $\mathrm {J} _{2n}(\alpha \rho ),$ sous forme d’intégrale définie suivant les sinus et cosinus des multiples de $\varphi .$ On sait que :

${\begin{aligned}e^{{\sqrt {-1}}\,\alpha \rho \,\sin \varphi }&=\mathrm {J} _{0}+2{\sqrt {-1}}\,\mathrm {J} _{1}\sin \varphi +2\mathrm {J} _{2}\cos 2\varphi +2{\sqrt {-1}}\,\mathrm {J} _{3}\sin 3\varphi \\[1ex]&=\mathrm {J} _{0}+2\sum \mathrm {J} _{2n}\cos 2n\varphi +2{\sqrt {-1}}\sum \mathrm {J} _{2n+1}\sin(2n+1)\varphi \\\end{aligned}}$

En développant $e^{{\sqrt {-1}}\,\alpha \rho \,\sin \varphi }$ par la formule de Fourier et comparant, il vient :

${\begin{aligned}2\pi \mathrm {J} _{0}&=\int _{0}^{2\pi }e^{{\sqrt {-1}}\,\alpha \rho \,\sin \varphi }\,d\varphi \\[1ex]2\pi \mathrm {J} _{2n}&=\int _{0}^{2\pi }e^{{\sqrt {-1}}\,\alpha \rho \,\sin \varphi }\cos 2n\varphi \,d\varphi \\\end{aligned}}$

Substituons ces valeurs dans l’expression de $\xi \,:$

$2\pi \xi =\int _{0}^{2\pi }e^{{\sqrt {-1}}\,\alpha \rho \,\sin \varphi }\sum \mathrm {A} _{2n}(-1)^{n}\cos 2n\varphi \,d\varphi$

Comme l’intégrale est définie et que les limites sont des constantes numériques nous pouvons changer $\varphi$ en $\omega$ et écrire :

${\begin{aligned}2\pi \xi &=\int _{0}^{2\pi }e^{{\sqrt {-1}}\,\alpha \rho \,\sin \omega }\sum \mathrm {A} _{2n}(-1)^{n}\cos 2n\omega \,d\omega \\[0.75ex]&=\int _{0}^{2\pi }\mathrm {B} e^{{\sqrt {-1}}\,\alpha \rho \,\sin \omega }\,d\omega .\\\end{aligned}}$

$\mathrm {B}$ et $\sin \omega$ ne changent pas quand on remplace $\omega$ par $\pi -\omega ,$ donc :

(3)

$2\pi \xi =2\int _{-{\frac {\pi }{2}}}^{+{\frac {\pi }{2}}}\mathrm {B} e^{{\sqrt {-1}}\,\alpha \rho \,\sin \omega }\,d\omega$

Or, nous avons trouvé :

${\begin{array}{rcl}\mathrm {Pour} \;\;0<\omega <\beta &&\mathrm {B} =\cos pt\\\pi -\beta <\omega <\pi &&\mathrm {B} =0\\\end{array}}$

Par conséquent, dans le plan focal, $\xi$ s’exprime donc par l’intégrale :

$\pi \xi =\int _{-\beta }^{+\beta }\cos pt\,e^{{\sqrt {-1}}\,\alpha \rho \,\sin \omega }\,d\omega$

analogue aux intégrales de Fresnel.

Il est à remarquer que la même méthode est applicable sans aucun changement si l’intensité du faisceau convergent au lieu d’être indépendante de $\omega$ dans toute l’étendue de ce faisceau et nulle à l’extérieur du faisceau comme nous l’avons supposé, variait suivant une loi tout à fait quelconque. La formule (3) serait encore vraie.

127. Ondes sphériques. — Soit une onde sphérique qui de convergente devient divergente.

Prenons le foyer comme origine des coordonnées polaires définies par :

${\begin{aligned}x&=r\sin \theta \cos \omega \\y&=r\sin \theta \sin \omega \\z&=r\cos \theta .\end{aligned}}$

Nous voulons trouver une fonction $\xi$ de $r,\,\theta ,\,\omega$ qui vérifie l’équation :

(1)

$\Delta \xi +\alpha ^{2}\xi =0$

À cet effet il est nécessaire de donner la définition des fonctions sphériques et quelques-unes de leurs propriétés.

On appelle fonction sphérique d’ordre $n$ une fonction $\mathrm {X} _{n}$ de $\theta$ et de $\omega ,$ qui multipliée par $r^{n}$ donne un polynôme $\mathrm {P} _{n}$ homogène de degré $n$ en $x,\,y,\,z$ et satisfaisant à l’équation

$\Delta \mathrm {P} _{n}=0$

Une fonction quelconque $\xi$ de $(r,\,\theta ,\,\omega )$ peut se mettre sous la forme :

$\xi =\sum \mathrm {F} _{n}\mathrm {X} _{n}$

$\mathrm {F} _{n}$ dépendant seulement de $r.$

Écrivons que $\xi$ vérifie l’équation (1) :

${\frac {d^{2}\xi }{dx^{2}}}=\sum {\frac {d^{2}(\mathrm {F_{n}X_{n}} )}{dx^{2}}}=\sum \mathrm {X} _{n}{\frac {d^{2}\mathrm {F} _{n}}{dx^{2}}}+2\sum {\frac {d\mathrm {X} _{n}}{dx}}{\frac {\mathrm {F} _{n}}{dx}}+\sum \mathrm {F} _{n}{\frac {d^{2}\mathrm {X} _{n}}{dx^{2}}}$

$\Delta \xi =\sum \mathrm {X} _{n}\Delta \mathrm {F} _{n}+2\sum \left({\frac {d\mathrm {X} _{n}}{dx}}{\frac {d\mathrm {F} _{n}}{dx}}+{\frac {d\mathrm {X} _{n}}{dy}}{\frac {d\mathrm {F} _{n}}{dy}}+{\frac {d\mathrm {X} _{n}}{dz}}{\frac {d\mathrm {F} _{n}}{dz}}\right)+\sum \mathrm {F} _{n}\Delta \mathrm {X} _{n}.$

Le second terme est nul, en effet :

${\frac {d\mathrm {F} _{n}}{dx}}={\frac {x}{r}}{\frac {d\mathrm {F} _{n}}{dr}},\;\mathrm {etc.}$

${\frac {d\mathrm {X} _{n}}{dx}}{\frac {d\mathrm {F} _{n}}{dx}}+{\frac {d\mathrm {X} _{n}}{dy}}{\frac {d\mathrm {F} _{n}}{dy}}+{\frac {d\mathrm {X} _{n}}{dz}}{\frac {d\mathrm {F} _{n}}{dz}}={\frac {1}{r}}{\frac {d\mathrm {F} _{n}}{dr}}\left[x{\frac {d\mathrm {X} _{n}}{dx}}+y{\frac {d\mathrm {X} _{n}}{dy}}+z{\frac {d\mathrm {X} _{n}}{dz}}\right]$

Mais d’après le théorème des fonctions homogènes le facteur entre $\left[\quad \right]$ est nul : car $\mathrm {X} _{n}$ est une fonction homogène de degré $0$ de $(x,\,y,\,z),$ puisque $\theta$ et $\omega$ sont de degré $0$ en $(z\,y\,x)$ et que $\mathrm {X} _{n}$ ne dépend pas de $r.$

Donc :

$\Delta \xi =\sum \mathrm {X} _{n}\Delta \mathrm {F} _{n}+\sum \mathrm {F} _{n}\Delta \mathrm {X} _{n}.$

D’après la définition des fonctions sphériques :

(2)

$0=\Delta \mathrm {P} _{n}=\Delta r^{n}\mathrm {X} _{n}=\mathrm {X} _{n}\Delta r^{n}+r^{n}\Delta \mathrm {X} _{n}.$

Si $\mathrm {F} _{n}$ ne dépend que de $r\,:$

$\Delta \mathrm {F} _{n}={\frac {d^{2}\mathrm {F} _{n}}{dr^{2}}}+{\frac {2}{r}}\,{\frac {d\mathrm {F} _{n}}{dr}}\cdot$

Appliquons cette formule à $r^{n}\,:$

$\Delta r^{n}=n(n-1)r^{n-2}+2nr^{n-2}=n(n+1)r^{n-2}.$

Remplaçons $\Delta r^{n}$ par sa valeur dans (2) :

$0=\mathrm {X} _{n}n(n+1)r^{n-2}+r^{n}\Delta \mathrm {X} _{n}$

(3)

${\frac {\Delta \mathrm {X} _{n}}{\mathrm {X} _{n}}}=-{\frac {n(n+1)}{r^{2}}}\cdot$

Tirons de cette équation la valeur de $\Delta \mathrm {X} _{n}$ et portons-la dans $\Delta \xi ,$ il vient :

(4)

$\Delta \xi =\sum \mathrm {X} _{n}\left(\Delta \mathrm {F} _{n}-{\frac {n(n+1)}{r^{2}}}\,\mathrm {F} _{n}\right)\cdot$

L’équation (1) peut alors se mettre sous la forme :

(5)

$\sum \mathrm {X} _{n}\left[{\frac {d^{2}\mathrm {F} _{n}}{dr^{2}}}+{\frac {2}{r}}{\frac {d\mathrm {F} _{n}}{dr}}+\mathrm {F} _{n}\left(\alpha ^{2}-{\frac {n(n+1)}{r^{2}}}\right)\right]=0.$

Le premier membre doit être nul identiquement, ce qui exige que le terme général soit nul. La fonction $\mathrm {F} _{n}$ doit donc vérifier l’équation différentielle :

(6)

${\frac {d^{2}\mathrm {F} _{n}}{dr^{2}}}+{\frac {2}{r}}{\frac {d\mathrm {F} _{n}}{dr}}+\mathrm {F} _{n}\left(\alpha ^{2}-{\frac {n(n+1)}{r^{2}}}\right)=0.$

La seule solution de cette équation qui reste finie pour $r=0$ est un polynôme entier en $\cos \alpha r,$ $\sin \alpha r,$ et ${\frac {1}{r}}\cdot$

Posons :

$\mathrm {U} _{n}={\frac {\mathrm {D} ^{n}(u^{2}-1)^{n}}{2^{n}n!}}$

$\mathrm {R} _{n}=\int _{-1}^{+1}e^{{\sqrt {-1}}\,\alpha ru}\mathrm {U} _{n}\left({\sqrt {-1}}\right)^{n}\,du.$

Cette expression est une fonction de $r\,;$ c’est un polynôme entier en $e^{{\sqrt {-1}}\,\alpha r},$ $e^{-{\sqrt {-1}}\,\alpha r}$ et ${\frac {1}{r}},$ par suite en $\cos \alpha r,$ $\sin \alpha r$ et ${\frac {1}{r}},$ c’est la solution cherchée.

On vérifie d’ailleurs aisément que l’on a :

$\mathrm {R} _{n}={\sqrt {\frac {\pi }{2\alpha r}}}\,\mathrm {J} _{n+{\frac {1}{2}}}(\alpha r)\cdot$

Donc

$\mathrm {F} _{n}=\mathrm {A} _{n}\mathrm {R} _{n},$

$\mathrm {A} _{n}$ ne dépendant que du temps et

$\xi =\sum \mathrm {A} _{n}\mathrm {R} _{n}\mathrm {X} _{n}.$

Les fonctions sphériques contiennent, comme cas particuliers, les polynômes de Legendre.

$\mathrm {X} _{n}(\theta )={\frac {\mathrm {D} ^{n}}{(d\cos \theta )^{n}}}{\frac {\left(\cos ^{2}\theta -1\right)^{n}}{2^{n}n!}}\cdot$

Pour déterminer $\mathrm {A} _{n}$ on pourrait procéder comme dans le cas précédent.

Lorsque $r$ est très grand, le premier terme de $\mathrm {R} _{n}$ contenant ${\frac {1}{r}},$ est seul sensible et la valeur asymptotique de $\mathrm {R} _{n}$ s’exprime par :

${\begin{array}{ll}\mathrm {R} _{n}=\pm {\dfrac {\sin \alpha r}{r}}&\mathrm {pour} \;n\;\mathrm {pair} \,;\\[1ex]\mathrm {R} _{n}=\pm {\dfrac {\cos \alpha r}{r}}&\mathrm {pour} \;n\;\mathrm {impair} .\\\end{array}}$

Pour $r$ très grand nous aurons donc :

$r\xi =\sum \mathrm {A} _{2n}(-1)^{n}\sin \alpha r\;\mathrm {X} _{2n}+\sum \mathrm {A} _{2n+1}(-1)^{n}\cos \alpha r\;\mathrm {X} _{2n+1},$

ce que je puis écrire :

$r\xi =\mathrm {B} \sin \alpha r+\mathrm {C} \cos \alpha r$

avec

$\mathrm {B} =\sum \mathrm {A} _{2n}(-1)^{n}\mathrm {X} _{2n};\qquad \mathrm {C} =\sum \mathrm {A} _{2n+1}(-1)^{n}\mathrm {X} _{2n+1}.$

Mais en un point très éloigné du foyer nous pouvons regarder la lumière observée comme constituée par la superposition d’un faisceau convergent et d’un faisceau divergent.

Soit alors :

$r\xi =f_{1}(\omega ,\theta )\cos(\alpha r+pt)$

l’équation du faisceau convergent. La fonction $f_{1}(\omega ,\theta )$ peut être regardée comme une des données de la question. Soit :

$r\xi =f_{2}(\omega ,\theta )\cos(\alpha r-pt),$

celle du faisceau divergent. Nous devons avoir :

$\mathrm {B} \sin \alpha r+\mathrm {C} \cos \alpha r=f_{1}\cos(\alpha r+pt)+f_{2}\cos(\alpha r-pt),$

ou en identifiant :

${\begin{aligned}\mathrm {B} &=(f_{2}-f_{1})\sin pt\\[0.5ex]\mathrm {C} &=(f_{2}+f_{1})\cos pt.\\\end{aligned}}$

Quand on passe d’une direction à la direction diamétralement opposée, c’est-à-dire quand on change $\omega$ en $\omega +\pi ,$ et $\theta$ en $\pi -\theta ,$ $\mathrm {B}$ qui ne contient que des fonctions sphériques d’ordre pair ne changera pas, et $\mathrm {C}$ qui ne contient que des fonctions sphériques d’ordre impair changera de signe. On peut en conclure que :

$f_{2}(\omega ,\,\theta )=-f_{1}(\omega +\pi ,\,\pi -\theta ).$

On remarquera le changement de signe impliqué par cette formule ; c’est une confirmation des résultats des § 107 et suivants.

Connaissant $f_{2}$ et $f_{1},$ on en déduira sans peine $\mathrm {B}$ et $\mathrm {C}$ et par conséquent les coefficients $\mathrm {A} _{n}.$ La connaissance de ces coefficients permettrait d’étudier les phénomènes d’interférence au voisinage du foyer. On n’arriverait pas toutefois à une formule relativement simple et élégante, comme celle que nous avons obtenue dans le cas des ondes cylindriques.

128. Polarisation par diffraction. — On a attribué à cette question de la polarisation par diffraction une très grande importance, on espérait arriver par l’étude de ces phénomènes à décider entre la théorie de Fresnel et la théorie de Neumann, c’est-à-dire à décider si le plan de polarisation est perpendiculaire ou parallèle à la direction de la vibration.

Par une application inexacte du principe de Huyghens, on avait obtenu des résultats qui ne furent pas confirmés par l’expérience, et les espérances qu’on avait conçues ne se justifièrent point.

Voici à peu près comment on raisonnait pour appliquer le principe de Huyghens.

Supposons un écran plan : prenons le plan de cet écran
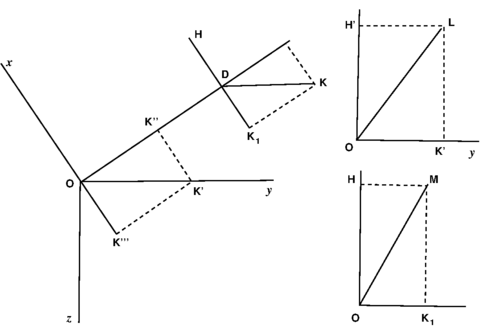
Fig. 30. comme plan des $xy\,:$ soient dans cet écran une ou plusieurs fentes parallèles à l’axe des $x,$ et indéfinies (c’est le cas d’un réseau). Sur cet écran tombe une onde plane parallèle au plan des $xy,$ c’est-à-dire un faisceau de rayons parallèles à $\mathrm {O} z.$ Soit $\mathrm {O} z$ un de ces rayons : par suite de la diffraction nous aurons de l’autre côté de l’écran des rayons déviés dans différentes directions, mais tous parallèles au plan des $yz.$ Nous appellerons ce plan des $yz$ plan de diffraction (fig. 30).

Considérons un de ces rayons diffractés $\mathrm {OD} .$ Deux cas sont à distinguer :

1^o Supposons la vibration incidente parallèle à $\mathrm {O} x,$ c’est-à-dire perpendiculaire au plan de diffraction par raison de symétrie ; sur le rayon diffracté, la vibration en un point $\mathrm {D}$ sera encore parallèle à $\mathrm {O} x,$ dirigée par exemple suivant $\mathrm {DH} ,$ seulement l’amplitude sera différente, elle sera diminuée dans un certain rapport ;

2^o Si la vibration incidente est parallèle à $\mathrm {O} y,$ c’est-à-dire parallèle au plan de diffraction, on ne peut pas admettre qu’en $\mathrm {D}$ la vibration soit encore parallèle à $\mathrm {O} y,$ puisqu’elle ne serait plus perpendiculaire au rayon $\mathrm {OD} .$

Décomposons la vibration incidente $\mathrm {OK} '$ en deux autres : l’une $\mathrm {OK} ''$ dirigée suivant le rayon $\mathrm {OD} ,$ l’autre $\mathrm {OK} '''$ perpendiculaire à $\mathrm {OD} .$ La vibration $\mathrm {OK} ''$ étant longitudinale ne sera pas transmise par l’éther ; seule la seconde sera transmise et en $\mathrm {D}$ nous aurons une vibration telle que $\mathrm {DK_{1}} ,$ perpendiculaire à $\mathrm {OD}$ dans le plan de diffraction. En appliquant les formules de Fresnel on trouve que :

${\frac {\mathrm {DH} }{\mathrm {OH} '}}={\frac {\mathrm {DK} }{\mathrm {OK} '}}={\frac {\mathrm {DK} _{1}}{\mathrm {OK} '''}}\cdot$

Le triangle $\mathrm {DKK} _{1}$ est donc rectangle et semblable au triangle $\mathrm {OK'K''} .$

Si la vibration $\mathrm {OL}$ n’est parallèle ni à $\mathrm {O} x$ ni à $\mathrm {O} y,$ on la décomposera en deux autres $\mathrm {OH}$ et $\mathrm {OK'}$ respectivement dirigées suivant ces axes.

Au point $\mathrm {D} ,$ $\mathrm {OH'}$ donnera une vibration $\mathrm {DH}$ parallèle à $\mathrm {O} x$ et $\mathrm {OK'}$ une vibration $\mathrm {DK} ,$ parallèle à $\mathrm {O} y.$ La résultante de ces deux vibrations est DM, et il est facile de voir que :

${\frac {\mathrm {DH} }{\mathrm {OH} '}}={\frac {\mathrm {DK} }{\mathrm {OK} '}}={\frac {\mathrm {DK} _{1}}{\mathrm {OK} '''}}={\frac {\mathrm {DK} _{1}}{\mathrm {OK} '\cos \theta }}$

ou

${\frac {\mathrm {DK} _{1}}{\mathrm {DH} }}={\frac {\mathrm {OK} '}{\mathrm {OH} '}}\,\cos \theta ,$

en appelant $\theta$ l’angle $z\mathrm {OD} .$

Donc

${\frac {\mathrm {DK} _{1}}{\mathrm {DH} }}<{\frac {\mathrm {OK} '}{\mathrm {OH} '}}$

ou

$\mathrm {tg} (\mathrm {HDM} )<\mathrm {tg} (\mathrm {H'OL} ).$

L’angle de la vibration avec $\mathrm {O} x$ diminue donc par le fait de la diffraction.

Si nous adoptons la théorie de Fresnel, le plan de polarisation est perpendiculaire à la vibration, la diffraction rapproche donc le plan de polarisation du plan de diffraction.

Dans la théorie de Neumann au contraire, le plan de polarisation étant parallèle à la vibration s’éloigne du plan de diffraction.

129. Cette opinion est encore assez répandue malgré les difficultés qu’ont rencontrées les expériences.

On admet que les théories de la réflexion et de la réfraction ne peuvent trancher la question, parce qu’elles nécessitent la connaissance des conditions aux limites, tandis que dans la diffraction il suffit d’appliquer le principe de Huyghens, sans que les conditions aux limites interviennent.

Cette opinion partagée par Stokes et Holtzmann ne peut se soutenir, comme nous allons le voir.

Rappelons en effet quel est l’énoncé exact du principe de Huyghens.

$\xi$ étant une fonction quelconque qui vérifie l’équation fondamentale

${\frac {d^{2}\xi }{dt^{2}}}=\mathrm {V} ^{2}\Delta \xi ,$

et peut représenter une composante de la vibration :

$\xi =\int \left({\frac {d\xi '}{dn}}\,\varphi -{\frac {d\varphi }{dn}}\,\xi '\right){\frac {d\omega '}{4\pi }},$

d’après les notations que nous avons adoptées. Cette relation a été démontrée rigoureusement en s’appuyant seulement sur l’équation fondamentale.

Si nous employons le langage de la théorie électromagnétique, $\mathrm {X,\,Y,\,Z}$ seront les composantes de la force électrique, $\alpha ,\,\beta ,\,\gamma$ celles de la force magnétique, et ces six fonctions vérifient l’équation fondamentale. Le théorème s’applique donc à ces six fonctions :

${\begin{aligned}\mathrm {X} &=\int \left({\frac {d\mathrm {X} '}{dn}}\,\varphi -{\frac {d\varphi }{dn}}\,\mathrm {X} '\right){\frac {d\omega '}{4\pi }}\\[1ex]\cdots &\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \;\mathrm {etc.} \\[1ex]\alpha &=\int \left({\frac {d\alpha '}{dn}}\,\varphi -{\frac {d\varphi }{dn}}\,\alpha '\right){\frac {d\omega '}{4\pi }}\\[1ex]\cdots &\cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \;\mathrm {etc.} \\\end{aligned}}$

Pour faire usage de ces formules nous avons supposé que sur la surface $\mathrm {S} ,$ dont une portion est occupée par l’écran, les valeurs de $\xi$ et de ${\frac {d\xi }{dn}}$ sont celles que donne la théorie géométrique des ombres : mais ce n’est là qu’une approximation, puisqu’en réalité, au voisinage de l’écran, se produisent des franges très fines, qui dépendent des conditions aux limites (cf. § 104), Pour voir si cette approximation est toujours légitime, voyons quelles en sont les conséquences, et pour cela appliquons ces formules à la polarisation par diffraction.

Si d’abord le plan de polarisation est parallèle au plan de diffraction, c’est-à-dire perpendiculaire aux fentes du réseau, la force électrique est parallèle à $\mathrm {O} x,$ et comme un plan perpendiculaire à $\mathrm {O} x$ est un plan de symétrie de la figure :

$\mathrm {Y} =\mathrm {Z} =0,$

la force électrique sera partout parallèle à Ox.

Si le plan de polarisation est perpendiculaire au plan de diffraction, la force magnétique parallèle au plan de polarisation sera parallèle à $\mathrm {O} x$ dans les rayons incidents ; par raison de symétrie, il en sera de même dans les rayons diffractés et

$\beta =\gamma =0.$

Dans le premier cas on peut appliquer la formule à $\mathrm {X} ,$ dans le second cas à $\alpha \,;$ en supposant que $\mathrm {X} ',$ ${\frac {d\mathrm {X} '}{dn}},$ $\alpha ',$ ${\frac {d\alpha '}{dn}}$ ont même valeur que dans la théorie géométrique des ombres, ce qui nous donnera une valeur approchée de $\mathrm {X}$ et de $\alpha .$

Dans le premier cas, la connaissance de $\mathrm {X}$ nous permettra de calculer facilement $\alpha ,\,\beta$ et $\gamma \,;$ de même dans le deuxième cas, connaissant $\alpha ,$ nous pourrons calculer $\mathrm {X,\,Y,\,Z}$ par les relations :

${\begin{aligned}\mathrm {K} {\frac {d\mathrm {X} }{dt}}&={\frac {d\gamma }{dy}}-{\frac {d\beta }{dz}}\\[1ex]\mathrm {K} {\frac {d\mathrm {Y} }{dt}}&={\frac {d\alpha }{dz}}-{\frac {d\gamma }{dx}}\\[1ex]\mathrm {K} {\frac {d\mathrm {Z} }{dt}}&={\frac {d\beta }{dx}}-{\frac {d\alpha }{dy}}\\\end{aligned}}$

qui ici se simplifient : en effet par raison de symétrie $\mathrm {X} =0$ et comme $\beta =\gamma =0,$ il reste seulement

(1)

${\begin{aligned}\mathrm {K} {\frac {d\mathrm {Y} }{dt}}&={\frac {d\alpha }{dz}}\\[1ex]\mathrm {K} {\frac {d\mathrm {Z} }{dt}}&=-{\frac {d\alpha }{dy}}\\\end{aligned}}$

130. Mais il peut sembler tout aussi légitime d’appliquer les mêmes procédés de calcul à la force magnétique dans le premier cas, ou à la force électrique dans le deuxième cas. Il est aisé de voir qu’on arrivera ainsi à des résultats tout à fait différents.

Plaçons-nous en effet dans le deuxième cas et appliquons le principe de Huyghens à la force électrique, il viendra :

${\begin{aligned}\mathrm {Y} &=\int \left({\frac {d\mathrm {Y} '}{dn}}\,\varphi -{\frac {d\varphi }{dn}}\,\mathrm {Y} '\right){\frac {d\omega '}{4\pi }}\\[1ex]\mathrm {Z} &=\int \left({\frac {d\mathrm {Z} '}{dn}}\,\varphi -{\frac {d\varphi }{dn}}\,\mathrm {Z} '\right){\frac {d\omega '}{4\pi }}\cdot \\\end{aligned}}$

Si l’on suppose que $\mathrm {Z} ',\,{\frac {d\mathrm {Z} '}{dn}},\,\mathrm {Y} '$ et ${\frac {d\mathrm {Y} '}{dn}}$ aient même valeur que dans la théorie géométrique des ombres, $\mathrm {Z} '$ et ${\frac {d\mathrm {Z} '}{dn}}$ devraient être nuls en tous les points de la surface $\mathrm {S} ,$ et par conséquent $\mathrm {Z}$ devrait être nul dans tout l’espace.

Or ce résultat est incompatible avec les équations (1).

$\mathrm {Z}$ ne peut être nul, puisque $\alpha$ est fonction de $y\,;$ d’ailleurs, s’il était nul, la condition de transversalité ne serait plus satisfaite.

On peut encore s’en rendre compte d’une manière un peu différente.

Dans le plan de l’écran, nous devons avoir comme partout :

${\frac {d\mathrm {X} }{dx}}+{\frac {d\mathrm {Y} }{dy}}+{\frac {d\mathrm {Z} }{dz}}=0$

ou comme $\mathrm {X} =0$

${\frac {d\mathrm {Y} }{dy}}+{\frac {d\mathrm {Z} }{dz}}=0.$

Or ${\frac {d\mathrm {Y} }{dy}}$ n’est pas nul ; en effet, si ${\frac {d\mathrm {Y} }{dy}}$ était nul, on aurait $\mathrm {Y} =\mathrm {const} ,$ ce qui est impossible puisque $\mathrm {Y}$ est nul sur les parties non éclairées ; il faut donc aussi que ${\frac {dZ}{dz}}\neq 0.$

131. Nous avons fait une hypothèse, à savoir que la théorie géométrique des ombres est applicable dans le plan de l’écran. D’après ce qui précède, cette hypothèse ne peut être légitime à la fois pour la force électrique et pour la force magnétique. Il n’y a aucune raison de supposer, comme on le fait d’ordinaire, qu’elle soit plus approchée pour l’un de ces deux vecteurs que pour l’autre, et encore bien moins que ce soit précisément pour celui des deux qui, dans la théorie élastique, représente en grandeur et direction la vibration des molécules d’éther.

Précédemment nous avions le droit de négliger les franges voisines de l’écran (cf. § 104) parce que ces franges étaient très fines vis-à-vis des franges situées à distance finie. Mais, quand il s’agit de la polarisation, deux cas peuvent se présenter : la déviation est très petite, ou elle a une valeur finie.

Si la déviation est très petite, l’approximation que nous avons faite est légitime, mais la rotation du plan de polarisation étant de l’ordre de $(1-\cos \theta )$ est très petite du deuxième ordre ; si $\theta$ est très petit, du premier ordre. On ne peut donc rien observer. Mais, au contraire, si la déviation est très grande, c’est qu’on a employé des réseaux à fentes extrêmement fines ; les franges anormales, voisines de l’écran, occupent alors une portion notable de la fente, et l’approximation n’est plus suffisante.

Les phénomènes étudiés par Stokes dépendent donc des conditions aux limites, tout comme les phénomènes de réflexion et de réfraction et pas plus qu’eux ne permettent de décider entre les théories de Fresnel et de Neumann.

132. Résultats des expériences. — Les expériences avec les réseaux présentent quelques difficultés ; les réseaux étant tracés sur verre, il y a à la fois réfraction et diffraction, et chacun de ces phénomènes fait tourner le plan de polarisation. Il y a lieu de se demander quel est celui qui précède l’autre.

Stokes a trouvé qu’aucune des deux formules ne représentait bien les expériences ; il a néanmoins conclu en faveur de la théorie de Fresnel. Holtzmann arrive au résultat opposé.

M. Eisenlohr a supposé que l’éther transmet les vibrations longitudinales, mais on les atténuant. Les formules s’accordent mieux avec les expériences, ce qui tient probablement à ce qu’elles renferment un paramètre de plus.

Enfin Quincke a trouvé des résultats très divergents, dépendant de la nature du réseau.

M. Gouy a réalisé des expériences, où il fait usage d’une méthode toute différente. L’écran est constitué par un biseau extrêmement aigu, tel que le tranchant d’un rasoir (fig. 31) ;
Fig. 31. à l’aide d’une lentille convergente $\mathrm {L} ,$ il concentre un faisceau de rayons lumineux, sur le bord même de l’écran. Une partie de ce faisceau est transmise directement, une autre est réfléchie sur le bord de l’écran et, enfin le reste est diffracté.

M. Gouy observe cette lumière diffractée, à l’aide d’un microscope $\mathrm {M}$ à long foyer, qui est mis au point sur le bord de l’écran et peut tourner autour d’un axe coïncidant avec le bord de l’écran. Il a pu ainsi observer des déviations atteignant $160$ degrés. Le maximum de lumière s’observe dans une direction faisant avec la seconde face du biseau un angle égal à l’angle du rayon incident avec la première face. Si nous appelons avec M. Gouy intérieure, la portion du faisceau comprise entre le faisceau transmis et la seconde face de l’écran, et extérieure, l’autre portion, nous trouverons que du côté intérieur la lumière diffractée est polarisée parallèlement au bord de l’écran, perpendiculairement au plan de diffraction ; du côté extérieur, au contraire, elle est polarisée perpendiculairement au bord de l’écran, parallèlement au plan de diffraction. La théorie de Stokes est impuissante à expliquer ces phénomènes. J’ai cherché s’il en serait de même d’une théorie plu» complète.

133. L’expérience montre que les phénomènes sont d’autant plus nets que le métal de l’écran est plus réfléchissant ou autrement dit se rapproche le plus d’être un conducteur parfait. Je me suis alors placé dans le cas limite où cet écran serait un conducteur parfait. Dans ces conditions la force électrique doit être perpendiculaire à l’écran. Supposons que la force électrique dans le rayon incident soit parallèle au bord de l’écran, c’est-à-dire que ce rayon soit polarisé dans le plan de diffraction ; par raison de symétrie, il en sera encore de même pour les rayons réfléchis et diffractés. La composante tangentielle de la force électrique doit être nulle sur la surface du conducteur. Ce conducteur a la forme d’un cylindre dont les génératrices sont perpendiculaires au plan de la figure. Donc la force électrique n’a pas de composante normale, et si la composante tangentielle est nulle, la force totale sera nulle aussi. La force électrique décroît donc quand on se rapproche de l’écran, ainsi que l’intensité de la lumière diffractée.

Supposons que la force magnétique $\alpha$ soit parallèle au bord de l’écran, la condition aux limites est que sur le bord de l’écran

${\frac {d\alpha }{dn}}=0,$

puisque la composante tangentielle de la force électrique est dans ce cas proportionnelle à ${\frac {d\alpha }{dn}}\cdot$ La lumière ne s’éteindra plus quand on se rapprochera des faces du biseau. La lumière polarisée parallèlement au bord de l’écran ne tend pas vers $0.$ Ces considérations font comprendre comment, si la lumière incidente est naturelle, la lumière diffractée du côté intérieur est polarisée parallèlement au bord de l’écran.

134. J’ai effectué le calcul en supposant que le bord de l’écran était un tranchant géométrique ; que l’angle du biseau était nul, que !a lumière incidente était concentrée par une lentille cylindrique et que l’angle du faisceau était nul.

Dans le cas où les rayons incidents et diffractés sont également inclinés sur les faces du biseau, $\delta$ étant la déviation comptée positivement vers l’intérieur, j’ai trouvé pour l’amplitude :

$1-{\frac {1}{\sin {\frac {1}{2}}\delta }}$

quand le plan de polarisation est parallèle au plan de diffraction, et

$1+{\frac {1}{\sin {\frac {1}{2}}\delta }}$

si ces deux plans sont perpendiculaires.

Pour $\delta =\pi$ la première composante est nulle. Quand on change $\delta$ en $-\delta ,$ les composantes s’échangent ; ce qui est conforme à l’observation.

Cependant il y a une difficulté : la première composante devient infinie pour $\delta =0.$ Cela tient sans doute à ce que le faisceau incident n’est pas, comme je l’ai supposé, limité par une surface géométrique.

Enfin M. Gouy a observé que la lumière diffractée avait une intensité maximum quand les angles des rayons incidents et diffractés avec les faces du biseau étaient égaux. La formule complète donne au contraire un minimum. Cela tient probablement à ce que le bord de l’écran est arrondi et qu’il faut faire intervenir non pas les angles, mais la longueur de l’arc compris entre les points de contact des deux rayons ; le maximum de lumière devant sans doute correspondre au minimum de cette longueur.

135. Il n’y a pas lieu, du reste, d’insister davantage sur cette comparaison entre la théorie et l’expérience ; car je n’ai pu faire le calcul qu’en me supposant placé dans des conditions très simples et, par conséquent, très éloignées de la réalité.

Mais il y a un point qui mérite d’attirer l’attention. La polarisation par diffraction est dans les expériences qui nous occupent beaucoup plus intense que la polarisation par réflexion. La théorie qui précède, quelque grossière qu’elle soit, nous permet de nous rendre compte de ce fait.

En effet, supposons-nous placés dans le cas limite d’une surface métallique parfaitement conductrice, et supposons de plus que la force électrique soit dans l’onde incidente perpendiculaire au plan de réflexion. À la surface du métal, la force électrique totale, qui est la somme algébrique de la force électrique incidente et de la force électrique réfléchie, devra être nulle. La force réfléchie sera donc égale en grandeur à la force incidente, et l’intensité de la lumière réfléchie sera égale à celle de la lumière incidente.

Mais dans le problème qui nous occupe les conditions sont très différentes, et ce qui intervient, ce n’est pas la force électrique réfléchie, mais la force électrique totale, laquelle est nulle. L’une des composantes disparaissant à peu près complètement, la polarisation est très intense.

En d’autres termes, il se produit entre le rayon incident et le rayon réfléchi une véritable interférence ; de telle sorte que, les deux rayons interférents étant presque naturels, le rayon résultant soit au contraire fortement polarisé.

C’est à cette explication, d’ailleurs, que M. Fizeau avait eu recours pour expliquer des phénomènes très curieux qu’il a décrits dans le tome LII des Comptes rendus et qui présentent, malgré leur plus grande complexité, une évidente parenté avec ceux qu’a découverts M. Gouy.

Une dernière remarque : j’ai employé le langage de la théorie électro-magnétique parce qu’il m’a paru plus commode. Mais il ne faudrait pas en conclure que les expériences de M. Gouy condamnent la théorie élastique, et confirment celle de Maxwell. Les deux théories conduisent aux mêmes équations. Tout ce que l’une explique, l’autre l’explique également. L’hypothèse sur laquelle reposait la théorie du § 128 est seule condamnée par ces expériences.

1. Pour plus de détails sur les propriétés de ces équations et des fonctions $\mathrm {J} _{0}(\rho ),$ voir Tisserand, Traité de mécanique céleste.