Leçons sur les hypothèses cosmogoniques (Poincaré, 1911)/Chapitre 05

Henri Poincaré

Leçons sur les hypothèses cosmogoniques

Libraire scientifique A. Hermann et fils, 1911 (p. 83-115).

CHAPITRE v.

HYPOTHÈSE DE M. DU LIGONDÈS.^[1]

---

67.Le point très original de la théorie de M. du Ligondès consiste dans l’idée qu’il se fait du chaos primitif :

« À l’origine l’Univers se réduisait à un chaos général extrêmement rare, formé d’éléments divers mus en tous sens et soumis à leurs attractions mutuelles…

« Ce chaos s’est partagé en lambeaux qui ont donné naissance, par voie de condensation progressive, à tous les Mondes de l’Univers. » (Formation mécanique du système du Monde, p. 14.)

Nous sommes loin, on le voit, de la nébuleuse de Laplace qui tournait tout d’une pièce avec une vitesse de rotation bien uniforme. Les tourbillons et gyrations intestines dont Faye dotait sa nébuleuse primitive sont aussi supprimés. Nous sommes, en quelque sorte, « revenus aux idées de Kant, avec le mouvement en plus, non pas le mouvement régulier de la rotation ou des tourbillons, mais le mouvement sans ordre apparent. » (p. 14.)

Nous devons donc nous représenter l’un quelconque des lambeaux nébuleux en lesquels le chaos initial s’est partagé, par suite de la tendance de toutes les molécules à se porter vers les régions les plus denses, comme formé par un très grand nombre de masses séparées, s’attirant les unes les autres, se mouvant en tous sens et pouvant arriver à se choquer de temps à autre. Les vitesses de tous ces projectiles ne sont soumises à aucune loi : la seule loi sera celle des grands nombres :

« Nous ne faisons aucune hypothèse sue la nature de ces mouvements ; nous les abandonnons entièrement à ce qu’on est convenu d’appeler le hasard. C’est en cela que l’hypothèse dont nous allons développer les conséquences diffère essentiellement de toutes celles qui ont été émises jusqu’ici ; c’est ce qui lui donne un caractère de vraisemblance et de généralité qui doit, a priori, la faire préférer à toute autre. L’hypothèse de Kant, malgré son apparente simplicité, est moins générale que la nôtre, puisque la matière y est primitivement en repos ; le repos n’est qu’un cas particulier du mouvement. » (p. 15.)

68.Examinons maintenant comment M. du Ligondès fait, d’un des lambeaux chaotiques, naître le système solaire.

Observons tout de suite — c’est là un point capital — que M. du Ligondès n’est pas en contradiction avec le principe des aires, comme l’était M. Kant qui supposait sa nébuleuse initiale partant du repos. Les projectiles dont se compose le lambeau ont leurs vitesses distribuées au hasard. Considérons alors les vecteurs qui représentent le moment de la quantité de mouvement de chacun de ces projectiles par rapport au centre de gravité du lambeau : ces vecteurs seront orientés dans tous les sens et auront des grandeurs diverses ; et, puisque le mouvement est supposé complètement désordonné, la somme géométrique de tous ces vecteurs sera très petite par rapport à leur somme arithmétique, c’est-à-dire par rapport à ce qu’elle serait si tous ces vecteurs avaient même direction ; mais en général elle ne sera pas nulle. Or, cette somme géométrique, c’est précisément le moment de rotation total du système, moment qui doit demeurer constant à partir de l’instant où le lambeau considéré est suffisamment séparé des autres pour pouvoir être regardé comme isolé. Il n’y a donc, a priori, aucune contradiction à faire sortir le système solaire d’un pareil lambeau nébuleux chaotique.

69.Cherchons à nous faire une idée de la somme géométrique et de la somme arithmétique des vecteurs dont nous venons de parler, et du rapport de ces deux sommes. La somme géométrique, nous la connaissons, c’est le moment de rotation actuel du système solaire. Pour essayer d’évaluer grossièrement la somme arithmétique, assimilons la nébuleuse chaotique initiale à une sphère homogène ayant une masse $\mathrm {M}$ égale à la masse totale du système solaire, et un rayon $\mathrm {R}$ égal à 100 000 unités astronomiques^[2]. À l’intérieur d’une telle sphère homogène, l’attraction est proportionnelle à la distance au centre et toutes les molécules décrivent des ellipses dans le même temps. Pour calculer ce temps, considérons une molécule décrivant une orbite circulaire ayant justement pour rayon 100 000 unités. Cette molécule se mouvant comme si toute la masse de la nébuleuse était concentrée au centre, sa duré de révolution se calculera suivant la troisième loi de Képler : elle aura pour valeur (100 000)^{$^{\frac {3}{2}}$}, soit environ 30 millions d’années. Une molécule $m$ décrivant dans ce temps une ellipse d’axes $2a$ et $2b$ aura donc pour moment de rotation

$m={\frac {2\pi ab}{30\,000\,000}},$

et la somme arithmétique des moments de rotation de toutes les molécules sera

$\mathrm {S} _{a}={\frac {2\pi }{30\times 10^{6}}}\sum mab,$

la somme $\textstyle \sum$ étant étendue à toutes les molécules qui constituent la nébuleuse. Pour calculer cette somme nous aurions besoin de connaître l’ellipse décrite par chaque molécule. Or, nous n’avons pas la moindre idée de la façon dont varient ces ellipses d’une molécule à l’autre, et il semble difficile de faire à ce sujet une hypothèse qui puisse se justifier. Mais, cherchant ici seulement un ordre de grandeur, nous remarquons que, pour la plupart des molécules, $a$ et $b$ sont comparables au rayon $\mathrm {R}$ de la nébuleuse sphérique et nous nous contentons d’écrire, avec une approximation grossière

${\begin{aligned}\mathrm {S} _{a}&={\frac {2\pi \mathrm {R} ^{2}}{30\times 10^{6}}}\sum m\\[0.5ex]&={\frac {2\pi \mathrm {R} ^{2}}{30\times 10^{6}}}\mathrm {M} .\end{aligned}}$

Quant à la somme géométrique $\mathrm {S} _{g}$, qui est le moment de rotation du système solaire, voici comment on peut l’évaluer. Le calcul montre que la sphère, homogène de rayon $\mathrm {R} =$ 100 000 unités devrait, pour avoir un moment de rotation égal à celui du système solaire, tourner sur elle-même d’un seul bloc en 10¹² années. Son moment de rotation, égal au produit de son moment d’inertie par sa vitesse angulaire, aurait alors pour expression

$\mathrm {S} _{g}={\frac {2}{5}}\mathrm {MR} ^{2}\times {\frac {2\pi }{10^{12}}}\cdot$

Le rapport ${\frac {\mathrm {S} _{g}}{\mathrm {S} _{a}}}$ de la somme géométrique à la somme arithmétique des moments de rotation des molécules est donc de l’ordre de 30 × 10⁶/10¹², soit à peu près de l’ordre de 1/30 000^[3].

Il faut donc penser que, dans le lambeau nébuleux chaotique d’où est sorti le système solaire, le hasard a établi cette légère prédominance des moments de rotation dans un certain sens. Pour d’autres lambeaux, la prédominance a pu être plus forte : ce fut le cas de ceux qui ont donné naissance à des systèmes d’étoiles doubles. M. du Ligondès remarque en effet que les étoiles doubles ont en général un moment de rotation beaucoup plus grand^[4] que celui du système solaire (car, pour ce dernier, la masse presque totale du système se trouve concentrée près du centre de gravité).

70.Chaque molécule décrivant approximativement une ellipse autour du centre de la nébuleuse, l’état chaotique persisterait indéfiniment s’il ne se produisait pas de chocs entre les différents projectiles. Mais ces projectiles se rencontreront inévitablement de temps à autre, et de leurs chocs résultera un double effet :

1^o Une concentration de la nébuleuse, une tendance à la formation d’un noyau central se produira, car deux projectiles qui se heurtent se collent ensemble et n’en forment plus qu’un ; il y a perte de force vive, ce qui se traduit par une chute des matériaux vers le centre.

2^o Le sphéroïde qu’est la nébuleuse chaotique initiale s’aplatira. Considérons, en effet, le plan du maximum des aires, perpendiculaire au moment de rotation résultant du système. Parallèlement à ce plan il y a (pour ainsi dire par définition) une légère prépondérance de molécules tournant dans un certain sens, tandis que parallèlement à un plan perpendiculaire à celui-là, cette prépondérance n’existe pas. Les chances de chocs seront donc moins nombreuses dans le plan équatorial du maximum des aires, où le mouvement est un peu orienté, que dans un plan méridien, où les mouvements se font indifféremment dans tous les sens. Il en résulte évidemment une tendance du sphéroïde à s’aplatir suivant la perpendiculaire au plan du maximum des aires.

71.Montrons que cet aplatissement, une fois commencé, va s’accentuer. Assimilons la nébuleuse aplatie à un ellipsoïde homogène. À l’intérieur d’un tel ellipsoïde, l’attraction au point $x,\,y,\,z$ a pour composantes

$-\alpha ^{2}x,\qquad -\beta ^{2}y,\qquad -\gamma ^{2}z,$

$\alpha ^{2},\,\beta ^{2},\,\gamma ^{2}$ étant trois constantes^[5]. La trajectoire d’une molécule quelconque sera définie par les équations différentielles

(1)

$\left\{{\begin{aligned}{\frac {d^{2}x}{dt^{2}}}+\alpha ^{2}x&=0,\\[0.5ex]{\frac {d^{2}y}{dt^{2}}}+\beta ^{2}y&=0,\\[0.5ex]{\frac {d^{2}z}{dt^{2}}}+\gamma ^{2}z&=0,\end{aligned}}\right.$

dont les intégrales générales sont

${\begin{alignedat}{3}x&=\mathrm {A} &&\cos \alpha t{}+{}\mathrm {B} &&\sin \alpha t,\\y&=\mathrm {A} _{1}&&\cos \beta t{}+{}\mathrm {B} _{1}&&\sin \beta t,\\z&=\mathrm {A} _{2}&&\cos \gamma t{}+{}\mathrm {B} _{2}&&\sin \gamma t.\end{alignedat}}$

La trajectoire donne donc, en projection sur chaque axe, un mouvement pendulaire simple, mais les périodes de ces trois mouvements pendulaires ne sont pas égales. On aura donc dans l’espace une courbe analogue aux courbes connues, dans le plan, sous le nom de courbes de Lissajous.

Dans le cas actuel les trois constantes $\alpha ,$ $\beta ,$ $\gamma$ varient lentement avec le temps, puisque l’ellipsoïde commence par s’aplatir. Nous sommes donc en présence d’une question analogue à celle qui a été étudiée au Chapitre précédent (n^o 64, p. 75). Si nous posons

$\mathrm {H} (x,t)={\frac {\alpha ^{2}x^{2}}{2}},$

la première équation (1) s’écrit

${\frac {d^{2}x}{dt^{2}}}+{\frac {d\mathrm {H} }{dx}}=0.$

Si $\mathrm {H}$ ne dépendait pas de $t,$ cette équation multipliée par ${\frac {dx}{dt}}$ et intégrée donnerait l’équation des forces vives

${\frac {1}{2}}\left({\frac {dx}{dt}}\right)^{2}+\mathrm {H} =\mathrm {T} ,$

où $\mathrm {T}$ serait une constante. Ici, où $\mathrm {H}$ varie lentement avec $t,$ nous posons cette même équation, qui servira de définition à $\mathrm {T} .$ La dérivée de $\mathrm {T}$ par rapport au temps est alors

${\frac {d\mathrm {T} }{dt}}={\frac {d\mathrm {H} }{dt}}={\frac {x^{2}}{2}}{\frac {d(\alpha ^{2})}{dt}}\cdot$

Pendant une oscillation ${\frac {d(\alpha ^{2})}{dt}}$ peut être regardé comme constant, et $x^{2}$ a pour valeur moyenne ${\frac {x_{0}^{2}}{2}},$ $x_{0}$ désignant l’élongation maxima ; on a donc pour la valeur moyenne de ${\frac {d\mathrm {T} }{dt}}$ pendant une oscillation

(2)

${\frac {d\mathrm {T} }{dt}}={\frac {x_{0}^{2}}{4}}{\frac {d(\alpha ^{2})}{dt}}\cdot$

D’autre part, ${\frac {dx}{dt}}$ s’annulant pour $x=x_{0},$ la constante des forces vives $\mathrm {T}$ a pour valeur

$\mathrm {T} =\mathrm {H} _{0}={\frac {\alpha ^{2}x_{0}^{2}}{2}},$

d’où

(3)

${\frac {d\mathrm {T} }{dt}}={\frac {\alpha ^{2}}{2}}{\frac {d(x_{0}^{2})}{dt}}+{\frac {x_{0}^{2}}{2}}{\frac {d(\alpha ^{2})}{dt}}\cdot$

La comparaison des équations (2) et (3) donne

${\frac {\alpha ^{2}}{2}}{\frac {d(x_{0}^{2})}{dt}}+{\frac {x_{0}^{2}}{4}}{\frac {d(\alpha ^{2})}{dt}}=0,$

c’est-à-dire

$\alpha {\frac {d(x_{0}^{2})}{dt}}+x_{0}^{2}{\frac {d\alpha }{dt}}=0,$

ou encore

$x_{0}^{2}\alpha ={\text{const.}}$

Donc, quand $\alpha$ augmente, l’amplitude des oscillations parallèlement à l’axe des $x$ diminue. Or, quand l’ellipsoïde, en gardant la même masse, s’aplatit suivant l’axe des $x,$ $\alpha$ augmente visiblement. En réalité, dans le cas actuel, $\alpha ,$ $\beta$ et $\gamma$ vont tous trois en augmentant, mais c’est $\alpha$ qui augmente le plus vite si l’axe des $x$ est perpendiculaire au plan du maximum des aires. L’aplatissement commencé s’accentuera donc de plus en plus.

72.C’est ainsi que M. du Ligondès rend compte du double fait d’une condensation centrale et d’une tendance à l’aplatissement ; le noyau central donnera le Soleil, et les matériaux extérieurs donneront autour de lui une sorte de disque lenticulaire équatorial qui, s’aplatissant de plus en plus, deviendra lui-même instable : ce disque pourra se résoudre finalement en anneaux qui se transformeront en planètes.

Nous avons ainsi expliqué la tendance des trajectoires à s’orienter parallèlement au plan équatorial du maximum des aires. Mais pourquoi les trajectoires des différents projectiles tendent-elles à devenir et à rester circulaires ? Lorsqu’un projectile en heurte un autre, il y a perte de force vive se traduisant par une diminution du grand axe de l’orbite de ce projectile. Cette diminution du grand axe est-elle accompagnée d’une diminution ou d’une augmentation de l’excentricité ? Pour nous en rendre compte, supposons qu’un de nos projectiles soit très gros (ce sera, si l’on veut, une planète déjà presque formée), les autres étant relativement petits : le gros projectile subira alors, du fait de ses chocs contre tous les petits, un effet analogue à celui d’une résistance de milieu. Or, nous verrons au Chapitre suivant qu’une résistance de milieu a en général pour effet de diminuer l’excentricité de l’orbite de la planète qui la subit, c’est-à-dire de rapprocher cette orbite de la forme circulaire.

73.Si l’on compare la conception de M. du Ligondès à la théorie cinétique des gaz, on ne peut s’empêcher de remarquer un contraste frappant. M. du Ligondès remplit l’espace de projectiles qui le sillonnent en tous sens. Les chocs de ces projectiles produisent l’évolution du chaos, sa transformation en un système planétaire bien ordonné. Dans la théorie cinétique, les molécules des gaz sont de même assimilées à des boulets se croisant dans toutes les directions, mais leurs chocs, au lieu d’amener une différenciation, produisent au contraire l’homogénéité parfaite de la masse gazeuse. Nous sommes donc, semble-t-il, devant un paradoxe^[6], puisque des prémisses en apparence identiques conduisent, ici et là, à des conséquences diamétralement opposées. En réalité, dans les deux cas, le second principe de la thermodynamique (Principe de Carnot-Clausius, ou de dégradation de l’énergie) trouve son application, mais de deux façons différentes. En effet, les prémisses, quoi qu’il paraisse tout d’abord, ne sont nullement les mêmes : les projectiles de la théorie des gaz sont supposés parfaitement élastiques, tandis que les projectiles cosmiques de M. du Ligondès sont plutôt mous. Aussi, au moment du choc, deux molécules gazeuses rebondissent l’une sur l’autre comme deux balles élastiques, sans perte de force vive ; tandis que deux projectiles cosmiques qui se heurtent se collent ensemble avec dégagement de chaleur, et par suite avec perte de force vive. Différence de nature des projectiles, voilà la vraie cause de l’apparent paradoxe que nous signalions.

Mais il convient d’insister et de pousser plus loin ce parallèle entre la théorie cinétique des gaz et la Cosmogonie de M. du Ligondès.

74.Théorème du viriel. — Considérons un système mécanique formé d’un grand nombre de points matériels. Soient $m$ la masse de l’un d’eux, $x,$ $y,$ $z$ ses coordonnées, $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z}$ les composantes de la force qui agit sur lui. On a

${\begin{aligned}m{\frac {d^{2}x}{dt^{2}}}&=\mathrm {X} ,\\[0.75ex]m{\frac {d^{2}y}{dt^{2}}}&=\mathrm {Y} ,\\[0.75ex]m{\frac {d^{2}z}{dt^{2}}}&=\mathrm {Z} .\end{aligned}}$

Posons

$\mathrm {U} =\sum m\left(x{\frac {dx}{dt}}+y{\frac {dy}{dt}}+z{\frac {dz}{dt}}\right)$

et

$\mathrm {V} =\sum m\left(x\mathrm {X} +y\mathrm {Y} +z\mathrm {Z} \right),$

les sommes $\textstyle \sum$ s’étendant à toutes les molécules. La quantité $\mathrm {V}$ s’appelle le viriel du système.

Calculons ${\frac {d\mathrm {U} }{dt}}$ :

${\frac {d\mathrm {U} }{dt}}\!=\!\sum \!m\!\left[\left({\frac {dx}{dt}}\right)^{2}\!\!+\!\left({\frac {dy}{dt}}\right)^{2}\!\!+\!\left({\frac {dz}{dt}}\right)^{2}\right]\!+\!\sum \!m\!\left(x{\frac {d^{2}x}{dt^{2}}}\!+\!y{\frac {d^{2}y}{dt^{2}}}\!+\!z{\frac {d^{2}z}{dt^{2}}}\right).$

La première somme $\textstyle \sum$ n’est autre que la force vive $2\mathrm {T} ,$ la seconde somme n’est autre que le viriel $\mathrm {V} .$ On a donc

(4)

${\frac {d\mathrm {U} }{dt}}=2\mathrm {T} +\mathrm {V} .$

Supposons que tous les points restent à distance finie et que leurs vitesses restent aussi finies : dans ce cas $\mathrm {U}$ sera toujours fini. Prenant les valeurs moyennes des deux membres de l’équation (4) pendant un intervalle de temps très long $t_{0}-t_{1},$ il vient

${\frac {1}{t_{1}-t_{0}}}(\mathrm {U} _{1}-\mathrm {U} _{0})={\text{moyenne de }}(2\mathrm {T} +\mathrm {V} ).$

Or, $\mathrm {U} _{1},\,\mathrm {U} _{0}$, valeurs de $\mathrm {U}$ aux époques $t_{1},$ $t_{0}$, sont finies, et $t_{1}-t_{0}$ est aussi grand qu’on le veut. On peut donc dire que pendant un temps très long la valeur moyenne du second membre est nulle : ce que nous écrivons, en surmontant les lettres d’un trait pour indiquer qu’il s’agit de valeurs moyennes,

(5)

$2{\overline {\mathrm {T} }}+{\overline {\mathrm {V} }}=0.$

Tel est le théorème du viriel.

75.Faisons d’abord l’application de ce théorème à un gaz renfermé dans un vase. Étant données deux molécules gazeuses m₁ et m₂, leur viriel a pour expression

$(x_{1}\mathrm {X} _{1}+y_{1}\mathrm {Y} _{1}+z_{1}\mathrm {Z} _{1})+(x_{2}\mathrm {X} _{2}+y_{2}\mathrm {Y} _{2}+z_{2}\mathrm {Z} _{2}).$

Quelles sont les forces $\mathrm {X} _{1},\,\mathrm {Y} _{1},\,\mathrm {Z} _{1},$ $\mathrm {X} _{2},\,\mathrm {Y} _{2},\,\mathrm {Z} _{2},$ appliquées à ces deux molécules ? Nous pouvons négliger les actions mutuelles des molécules, sauf aux moments des chocs, d’ailleurs au moment d’un choc on a

${\begin{aligned}x_{1}&=x_{2},&y_{1}&=y_{2},&z_{1}&=z_{2},\end{aligned}}$

puisque les deux molécules sont au contact ; et d’autre part

${\begin{aligned}\mathrm {X} _{1}+\mathrm {X} _{2}&=0,&\mathrm {Y} _{1}+\mathrm {Y} _{2}&=0,&\mathrm {Z} _{1}+\mathrm {Z} _{2}&=0.\end{aligned}}$

puisque la réaction est égale et opposée à l’action. Le viriel dû aux chocs des molécules entre elles est donc nul, au moins en première approximation^[7].

Mais il faut tenir compte aussi des chocs des molécules contre les parois du vase : à ces chocs est due la pression $p$ du gaz. La force exercée sur un élément $d\omega$ de surface dont la normale extérieure fait avec les axes les angles $\alpha ,$ $\beta ,$ $\gamma$ a pour composantes

${\begin{aligned}-p\cos \alpha \,d\omega &,&-p\cos \beta \,d\omega &,&-p\cos \gamma \,d\omega &.\end{aligned}}$

Le viriel ${\overline {\mathrm {V} }}$ dû aux chocs contre la paroi a donc pour expression

${\overline {\mathrm {V} }}=-p\iint (x\cos \alpha +y\cos \beta +\cos \gamma )\,d\omega ,$

l’intégrale étant étendue à toute la surface. Or, on a

$\iint x\cos \alpha \,d\omega =\iint y\cos \beta \,d\omega =\iint z\cos \gamma \,d\omega =v,$

$v$ désignant le volume total du vase ; par suite

${\overline {\mathrm {V} }}=-3pv,$

et l’équation (5) du viriel donne

$3pv=2{\overline {\mathrm {T} }}.$

Cette relation, due à Clausius, traduit la loi de Mariotte et Gay-Lussac, car la force vive moyenne $2{\overline {\mathrm {T} }}$ est proportionnelle à la température absolue du gaz.

76.Appliquons maintenant le théorème du viriel à la nébuleuse chaotique de M. du Ligondès. Ici nous n’avons plus de parois, mais nous ne pouvons plus négliger l’attraction mutuelle des projectiles. Appelant $r$ la distance de deux masses $m_{1}$ et $m_{2},$ nous désignons par

$\mathrm {W} =\sum _{i,k}m_{i}m_{k}\varphi (r)$

la fonction des forces. Calculons le viriel : la force $(\mathrm {X} _{i},\,\mathrm {Y} _{i},\,\mathrm {Z} _{i})$ qui s’exerce sur $m_{i}$ par suite de l’action de $m_{k}$ a pour composante suivant l’axe des $x$

$\mathrm {X} _{i}=m_{i}m_{k}\varphi '(r){\frac {x_{i}-x_{k}}{r}}\,;$

la masse $m_{i},$ fournit donc, dans le viriel, le terme

$\mathrm {X} _{i}x_{i}=m_{i}m_{k}\varphi '(r){\frac {x_{i}-x_{k}}{r}}x_{i}.$

La masse $m_{k}$ fournit de même le terme

$\mathrm {X} _{k}x_{k}=m_{i}m_{k}\varphi '(r){\frac {x_{k}-x_{i}}{r}}x_{k}.$

La somme de ces deux termes est

$m_{i}m_{k}\varphi '(r){\frac {(x_{i}-x_{k})^{2}}{r}}\cdot$

Nous voyons aisément que le viriel total a pour valeur

${\begin{aligned}\mathrm {V} &=\sum _{i,k}m_{i}m_{k}\varphi '(r){\frac {(x_{i}-x_{k})^{2}+(y_{i}-y_{k})^{2}+(z_{i}-z_{k})^{2}}{r}}\\[0.5ex]&=\sum _{i,k}m_{i}m_{k}\varphi '(r)r.\end{aligned}}$

Dans le cas de l’attraction newtonienne, nous avons

$\varphi (r)={\frac {1}{r}}$

et

$\varphi '(r)r=-{\frac {1}{r}}\,;$

par suite

${\begin{aligned}\mathrm {V} &=-\sum _{i,k}m_{i}m_{k}{\frac {1}{r}}\\[0.75ex]&=-\mathrm {W} .\end{aligned}}$

L’équation du viriel donne donc

$2\mathrm {\overline {T}} -\mathrm {\overline {W}} =0.$

D’ailleurs, nous pouvons écrire aussi l’équation des forces vives

$\mathrm {\overline {T}} -\mathrm {\overline {W}} =\mathrm {C} ,$

$\mathrm {C}$ restant constant tant qu’il n’y a pas de choc. De ces deux dernières égalités nous tirons

${\begin{aligned}\mathrm {\overline {T}} &=-\;\mathrm {C} ,\\[0.75ex]\mathrm {\overline {W}} &=-2\mathrm {C} .\end{aligned}}$

Que pouvons-nous conclure de là ? Supposons tout d’abord que les projectiles soient parfaitement élastiques : leurs chocs n’entraînent aucune perte de force vive, et $\mathrm {C}$ reste constant malgré ces chocs. Alors les valeurs moyennes de $\mathrm {T}$ et de $\mathrm {W}$ sont aussi constantes. Or,

$\mathrm {W} =-\sum _{i,k}{\frac {m_{i}m_{k}}{r}}$

augmente avec la concentration ; il n’y aura donc pas tendance à la formation d’un noyau central très condensé. Ce seraient là les conditions d’une masse gazeuse entièrement isolée dans l’espace : cette masse ne se concentre pas indéfiniment, elle admet un certain état final d’équilibre, auquel elle tend d’elle-même à revenir si elle s’en est écartée accidentellement. S’il se produit en un point une petite condensation anormale, elle tend à disparaître d’elle-même.

Au contraire, si les projectiles ont une certaine mollesse — et c’est le cas pour les matériaux cosmiques de M. du Ligondès — la constante des forces vives $\mathrm {C}$ décroît à chacun des chocs, par suite

$\mathrm {\overline {W}} =-2\mathrm {C}$

croîtra sans cesse : c’est dire que les distances $r$ décroîtront en moyenne, et par suite que les chocs provoquent une tendance à la concentration indéfinie^[8].

77.Loi de répartition des vitesses. — Avant de donner la loi de Maxwell sur la répartition des vitesses des molécules gazeuses dans la théorie cinétique, exposons quelques considérations préliminaires.

Envisageons un liquide enfermé dans un vase de forme invariable qu’il remplit complètement. Soient $x,$ $y,$ $z$ les coordonnées d’une molécule liquide, $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z}$ les composantes de sa vitesse, de telle façon que les équations différentielles des trajectoires des molécules s’écrivent

(6)

${\frac {dx}{\mathrm {X} }}={\frac {dy}{\mathrm {Y} }}={\frac {dz}{\mathrm {Z} }}=dt.$

$\mathrm {X} ,\,\mathrm {Y} ,\,\mathrm {Z}$ sont, par hypothèse, des fonctions données de $x,$ $y,$ $z$ et $t.$ Dans ce qui suit, le mouvement sera supposé permanent, en sorte que $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z}$ ne dépendront que de $x,$ $y,$ $z.$ Comme le liquide est incompressible, on aura

(7)

${\frac {d\mathrm {X} }{dx}}+{\frac {d\mathrm {Y} }{dy}}+{\frac {d\mathrm {Z} }{dz}}=0.$

Nous supposerons que le liquide est un mélange de deux autres liquides : un liquide blanc et un liquide rose, par exemple. Si, au début, ces deux liquides ne sont pas mélangés, on prévoit facilement qu’en général les brassages dus aux mouvements des molécules liquides auront pour effet de les mêler et de rendre finalement la masse homogène.

Parmi les molécules liquides distinguons-en un certain nombre (par exemple les molécules du liquide rose), et considérons leur distribution à une certaine époque $t$ à l’intérieur du vase. Appelons $\rho$ la densité du liquide rose^[9] au voisinage du point quelconque $x,\,y,\,z\,;$ nous conviendrons de dire que

$\rho \,dx\,dy\,dz$

est proportionnel à la probabilité pour qu’à l’époque $t$ une molécule rose soit intérieure au petit élément de volume $dx\,dy\,dz.$ La probabilité pour qu’à l’époque $t$ une molécule rose soit intérieure à un certain volume fini sera de même, par définition, proportionnelle à l’intégrale

$\iiint \rho \,dx\,dy\,dz$

étendue à ce volume.

Soit $\psi (x,y,z)$ une fonction quelconque. La valeur moyenne de cette fonction à l’instant $t$ pour les molécules roses sera par définition

${\frac {1}{\mathrm {V} }}\iiint \rho \,\psi (x,y,z)\,dx\,dy\,dz,$

$\mathrm {V}$ désignant le volume total du vase, et l’intégrale étant étendue à tout ce volume. Cette intégrale mesure, si l’on veut, l’espérance mathématique d’un joueur à qui l’on aurait promis une somme $\psi (x,\,y,\,z)$ chaque fois qu’une molécule rose sera intérieure au volume $dx\,dy\,dz.$

Au lieu de considérer l’ensemble des molécules roses à une certaine époque, on pourrait, si on le préférait, considérer une molécule déterminée et la suivre dans son mouvement pendant un temps très long $\mathrm {T} .$ La probabilité pour que cette molécule rose soit intérieure à un volume $v$ serait alors, par définition, le rapport à $\mathrm {T}$ du temps pendant lequel la molécule envisagée a été intérieure à ce volume. De même, la valeur moyenne d’une fonction $\psi$ serait définie comme étant la moyenne, pendant ce temps très long, des valeurs que donnent à $\psi (x,y,z)$ les coordonnées de la molécule en question.

Les mouvements des molécules liquides, définis par les équations (6), auront en général pour effet de faire tendre le liquide, au bout d’un temps suffisamment long, vers un état limite permanent. Dans cet état final la densité $\rho$ du liquide rose devenue indépendante de $t,$ comme le sont $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z} ,$ ne dépendra plus que de $x,$ $y,$ $z.$ Quelle sera cette distribution finale permanente des densités $\rho$ ? Écrivons l’équation de continuité relative au liquide rose

${\frac {d\rho }{dt}}+{\frac {d(\rho \mathrm {X} )}{dx}}+{\frac {d(\rho \mathrm {Y} )}{dy}}+{\frac {d(\rho \mathrm {Z} )}{dz}}=0\,;$

dans l’état final permanent, la dérivée partielle ${\frac {d\rho }{dt}}$ sera nulle ; et cette équation se réduira, en vertu de l’équation (7), à

$\mathrm {X} {\frac {d\rho }{dx}}+\mathrm {Y} {\frac {d\rho }{dy}}+\mathrm {Z} {\frac {d\rho }{dz}}=0.$

Cette équation n’interprète facilement : d’après les équations (6), $\mathrm {X} ,$ $\mathrm {Y} ,$ $\mathrm {Z}$ sont proportionnels aux composantes $dx,$ $dy,$ $dz$ du déplacement élémentaire de la molécule ; on a donc

${\frac {d\rho }{dx}}dx+{\frac {d\rho }{dy}}dy+{\frac {d\rho }{dz}}dz=0.$

Cette équation signifie que, quand l’état permanent est atteint, $\rho$ ne varie pas tout le long de la trajectoire d’une molécule quelconque.

Si donc une trajectoire quelconque remplit le vase tout entier^[10], l’état final permanent donnera

$\rho ={\text{const.}}$

dans tout le vase ; c’est-à-dire que le mouvement aura eu pour résultat le mélange complet des deux liquides. C’est le cas le plus général.

Mais il peut arriver que les équations données (6) admettent une intégrale première

$\mathrm {J} (x,y,z)={\text{const.}}$

Cette équation représente une famille de surfaces, et une trajectoire quelconque est alors située tout entière sur une telle surface. Si elle remplit cette surface, la densité $\rho$ sera constante sur cette surface et la distribution finale des densités sera représentée par

$\rho =f(\mathrm {J} ),$

$f$ étant une fonction quelconque.

De même, si les équations (6) admettent deux intégrales

${\begin{aligned}\mathrm {J} _{1}(x,y,z)&={\text{const.}}&\mathrm {J} _{2}(x,y,z)&={\text{const.}}\end{aligned}}$

on aura comme loi finale de distribution des densités

$\rho =f(\mathrm {J} _{1},\mathrm {J} _{2}).$

78.Après ces préliminaires, envisageons un système mécanique (S) à $n$ degrés de liberté. Sa situation à l’époque $t$ est définie par $n$ paramètres

$q_{1},\,q_{2},\,\dots \,\,q_{n}.$

Son énergie potentielle $\mathrm {U}$ est une fonction de ces variables $q_{i}$. Sa force vive $2\mathrm {T}$ est une fonction des $q_{i}$ et de leurs dérivées $q_{i}'$ par rapport au temps. Si nous posons

${\frac {d\mathrm {T} }{dq_{i}'}}=p_{i}$

nous aurons, pour définir le mouvement du système, les $2n$ équations différentielles suivantes (équations canoniques de Hamilton) :

(8)

${\begin{aligned}{\frac {dq_{i}}{dt}}&={\frac {d\mathrm {E} }{dp_{i}}},&{\frac {dp_{i}}{dt}}&=-{\frac {d\mathrm {E} }{dq_{i}}},\end{aligned}}$

où $\mathrm {E=T+U}$ représente l’énergie totale du système, fonction des $q_{i}$ et des $p_{i}.$ Posant pour abréger

${\begin{aligned}{\frac {d\mathrm {E} }{dp_{i}}}&=\mathrm {Q} _{i},&-{\frac {d\mathrm {E} }{dq_{i}}}&=\mathrm {P} _{i},\end{aligned}}$

les équations (8) s’écrivent

(9)

${\frac {dq_{i}}{\mathrm {Q} _{i}}}={\frac {dp_{i}}{\mathrm {P} _{i}}}=dt.$

Elles sont de la même forme que les équations (6), les $\mathrm {P} _{i}$ et les $\mathrm {Q} _{i}$ étant indépendants de $t.$ De plus, les $\mathrm {P} _{i}$ et les $\mathrm {Q} _{i}$ satisfont évidemment à l’équation

(10)

$\sum {\frac {d\mathrm {Q} _{i}}{dq_{i}}}+\sum {\frac {d\mathrm {P} _{i}}{dp_{i}}}=0,$

de même forme que l’équation d’incompressibilité (7).

Si donc nous considérons

$q_{1},\,q_{2},\,\dots \,q_{n},\,p_{1},\,p_{2},\,\dots \,p_{n}$

comme les coordonnées, dans un espace à $2n$ dimensions, d’une particule matérielle Π, dont la vitesse aurait pour composantes

$\mathrm {Q_{1},\,Q_{2},\,\dots ,\,Q_{n},\,P_{1},\,P_{2},\,\dots ,\,P_{n},}$

nous pourrons dire que les équations (9) sont les équations différentielles de la trajectoire de la particule Π.

Dans cet espace à $2n$ dimensions, considérons fictivement un vase complètement rempli par un liquide incompressible, les molécules de ce liquide se mouvant conformément aux équations (9). Comme les composantes de la vitesse de la particule Π satisfont à l’équation (10) d’incompressibilité, nous pouvons considérer cette particule Π comme étant en suspension dans un pareil liquide fictif qui l’entraîne dans son mouvement.

Ainsi, au mouvement de notre système mécanique (S), nous faisons correspondre, dans l’espace à $2n$ dimensions, la trajectoire d’une particule Π en suspension dans un fluide incompressible.

Si, au lieu d’un seul système mécanique (S), nous en considérons un très grand nombre

(S₁), (S₂), …, (S_m),

obéissant aux mêmes équations (9) de mouvement, mais différant entre eux par les conditions initiales, au lieu d’une seule particule Π, nous aurons à en considérer $m$

Π₁, Π₂, …, Π_m,

toutes en suspension dans le même liquide incompressible. Ces particules Π vont jouer ici le rôle des molécules roses que nous considérions un peu plus haut.

Définissons la probabilité pour qu’à un instant donné $t$, un de nos systèmes pris au hasard parmi nos $m$ systèmes satisfasse à certaines conditions, par exemple pour que sa particule représentative Π soit intérieure à un certain volume $v$ de l’espace à $2n$ dimensions. Si, à cette époque $t$, la densité des particules Π est représentée par $\rho$^[11], la probabilité en question sera, par définition, proportionnelle à l’intégrale $2n$ uple

$\iint \dots \int \rho \,dq_{1}\,dq_{2}\,\dots \,dq_{n}\,dp_{1}\,dp_{2}\,\dots \,dp_{n}$

étendue à ce volume $v$.

Soit $\psi (q_{1},\,q_{2},\,\,\dots \,q_{n},\,p_{1},p_{2},\,\,\dots \,p_{n})$ une fonction quelconque. Sa valeur moyenne, à l’instant $t,$ pour les particules Π sera, par définition,

${\frac {1}{\mathrm {V} }}\iint \dots \int \rho \,\psi \,dq_{1}\,dq_{2}\,\dots \,dq_{n}\,dp_{1}\,dp_{2}\,\dots \,dp_{n},$

$\mathrm {V}$ désignant le volume total du vase dans l’espace à $2n$ dimensions et l’intégrale étant étendue à tout ce volume.

Au lieu de considérer simultanément les $m$ systèmes

(S₁), (S₂), …, (S_m),

on pourrait, si on le préférait, considérer seulement l’un d’entre eux, et le suivre dans son mouvement pendant un temps très long $\mathrm {T} ,$ entre les époques $t_{0}$ et $t_{0}+\mathrm {T} .$ La probabilité pour que ce système satisfasse à certaines conditions serait alors, par définition, le rapport à $\mathrm {T}$ du temps pendant lequel il a satisfait à ces conditions entre les époques $t_{0}$ et $t_{0}+\mathrm {T} .$ On définirait de même la valeur moyenne d’une fonction $\psi (q_{1},\,q_{2},\,\,\dots \,q_{n},\,p_{1},\,p_{2},\,\,\dots \,p_{n})$ comme étant la moyenne, pendant ce temps très long $\mathrm {T} ,$ des valeurs que donnent à $\psi$ les coordonnées de la particule Π représentative du système.

Le liquide fictif de l’espace à $2n$ dimensions va, en général, quelles que soient les conditions initiales, par suite des mouvements intérieurs définis par les équations (9), tendre vers un état limite permanent, comme il arrivait précédemment dans le cas simple de trois dimensions. Le raisonnement fait dans ce cas simple (p. 97) est évidemment général et nous permet de dire qu’une fois l’état permanent atteint, la densité $\rho$ des particules Π ne variera pas tout le long de la trajectoire d’une molécule quelconque.

Si donc une de ces trajectoires emplit le vase tout entier la distribution finale des densités $\rho$ sera

$\rho ={\text{const.}}$

dans tout le vase. Si les équations (9) de mouvement admettent une intégrale première

$\mathrm {J} ={\text{const.}}$

cette distribution finale sera

$\rho =f(\mathrm {J} ).$

Si les équations (9) admettent $k$ intégrales premières

$\mathrm {J} _{1}={\text{const.}},\;\mathrm {J} _{2}={\text{const.}},\;\dots \;\mathrm {J} _{k}={\text{const.}},$

la distribution finale sera

$\rho =f(\mathrm {J} _{1},\,\mathrm {J} _{2},\,\dots ,\,\mathrm {J} _{k})$

Toutefois cette dernière affirmation suppose implicitement que la trajectoire d’une des molécules, qui est située tout entière sur la multiplicité à $2n-k$ dimensions définie par les équations

$\mathrm {J} _{1}={\text{const.}},\;\mathrm {J} _{2}={\text{const.}},\;\dots \;\mathrm {J} _{k}={\text{const.}},$

remplit celle multiplicité. Nous admettrons — c’est en cela que consiste le « postulat de Maxwell » — qu’il en est effectivement ainsi pour les systèmes que nous considérons.

79.Dans le cas qui nous occupe, les équations (8) ou (9) du mouvement admettent une intégrale, celle des forces vives

$\mathrm {E} ={\text{const.}}$

Supposons d’abord que ce soit la seule. La loi de distribution finale des densités $\rho$ est alors

$\rho =f(\mathrm {E} ).$

Supposons un instant, pour simplifier et pour avoir une représentation géométrique, que notre espace n’a que trois dimensions ; alors l’intégrale

$\mathrm {E} ={\text{const.}}$

représente une famille de surfaces ; la loi

$\rho =f(\mathrm {E} )$

nous enseigne que $\rho$ est constant tout le long d’une telle surface, mais peut varier d’une surface à l’autre. Considérons deux surfaces

voisines $\mathrm {E}$ et $\mathrm {E} +d\mathrm {E}$ (fig. 17) ; les normales à $\mathrm {E}$ le long du contour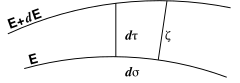

fig.17. d’un petit élément de surface $d\sigma$ définissent, entre ces deux surfaces, un élément de volume

$d\tau =\zeta \,d\sigma ,$

$\zeta$ représentant la distance qui sépare les deux surfaces. La probabilité pour qu’une particule Π soit intérieure à cet élément $d\tau$ est par définition proportionnelle à

$\rho \,d\tau =\rho \zeta \,d\sigma$

de sorte que, si nous restons constamment sur la même surface $\mathrm {E} ,$ nous pouvons dire que la densité superficielle le long de cette surface est représentée par

$\rho '=\rho \zeta \,;$

elle est proportionnelle à $\zeta$, qui visiblement est lui-même proportionnel à

${\frac {1}{\dfrac {d\mathrm {E} }{dn}}}={\frac {1}{\sqrt {\left({\dfrac {d\mathrm {E} }{dx}}\right)^{2}+\left({\dfrac {d\mathrm {E} }{dy}}\right)^{2}+\left({\dfrac {d\mathrm {E} }{dz}}\right)^{2}}}}\cdot$

Restant encore dans le cas de trois dimensions, supposons maintenant que les équations de mouvement admettent deux intégrales

${\begin{aligned}\mathrm {J} _{1}&={\text{const.}},&\mathrm {J} _{2}&={\text{const.}}\end{aligned}}$

L’ensemble de ces deux équations représente une famille de courbes le long desquelles $\rho$ reste constant, tout en pouvant varier d’une courbe à l’autre. Assujettissons $\mathrm {J} _{1}$ à rester compris entre $\mathrm {J} _{1}^{0}$ et $\mathrm {J} _{1}^{0}+d\mathrm {J} _{1}^{0}$, et $\mathrm {J} _{2}$ à rester compris entre entre $\mathrm {J} _{2}^{0}$ et $\mathrm {J} _{2}^{0}+d\mathrm {J} _{2}^{0}$. Nous définissons ainsi un petit tube dont nous appelons $\zeta$ la section droite. Nous pouvons alors prendre des éléments de volume

$d\tau =\zeta \,d\sigma ,$

$d\sigma$ représentant ici l’élément linéaire de la courbe

${\begin{aligned}\mathrm {J} _{1}&=\mathrm {J} _{1}^{0},&\mathrm {J} _{2}&=\mathrm {J} _{2}^{0},\end{aligned}}$

ce qui nous amène à définir le long de cette courbe une densité linéaire

$\rho '=\rho \zeta ,$

proportionnelle à la section droite $\zeta$ du tube ; et ici l’on aura ${\frac {1}{\zeta ^{2}}}$ proportionnel à

$\left[{\frac {\mathrm {D} (\mathrm {J} _{1},\mathrm {J} _{2})}{\mathrm {D} (y,z)}}\right]^{2}+\left[{\frac {\mathrm {D} (\mathrm {J} _{1},\mathrm {J} _{2})}{\mathrm {D} (z,x)}}\right]^{2}+\left[{\frac {\mathrm {D} (\mathrm {J} _{1},\mathrm {J} _{2})}{\mathrm {D} (x,y)}}\right]^{2}\cdot$

Plaçons-nous à présent dans le cas général d’un espace à $2n$ dimensions, et supposons que les équations de mouvement (9) admettent $k$ intégrales

$\mathrm {J} _{1}={\text{const.}},\quad \mathrm {J} _{2}={\text{const.}},\quad \dots ,\quad \mathrm {J} _{k}={\text{const.}}.$

L'ensemble de ces $k$ équations définit une fusille de multiplicités à $2n-k$ dimensions, le long desquelles $\rho$ est constant, tout en pouvant varier de l’une à l’autre. Nous pourrons encore considérer un élément $d\sigma$ d’une de ces multiplicités, et chercher une densité fictive $\rho '$ correspondante : nous trouverons encore

$\rho '=\rho \zeta ,$

${\frac {1}{\zeta ^{2}}}$ étant ici proportionnel à

$\sum \Delta ^{2},$

où les $\Delta$ sont les différents jacobiens d’ordre $k$ qu’on peut former avec les $k$ fonctions $\mathrm {J}$ et les $2n$ variables $q_{i}$ et $p_{i}.$

Le résultat serait le même, et nous trouverions la même densité, fictive $\rho ',$ si nous posions le problème d’une façon un peu différente. Supposons que les équations de mouvement (9), au lieu d’admettre $k$ intégrales, en admettent seulement $h$

(11)

$\mathrm {J} _{1}={\text{const.}},\quad \mathrm {J} _{2}={\text{const.}},\quad \dots ,\quad \mathrm {J} _{h}={\text{const.}}\,;$

mais nous imposons à notre système l’obligation de satisfaire à $k-h$ autres conditions

(12)

$\mathrm {J} _{h+1}={\text{const.}},\quad \mathrm {J} _{h+2}={\text{const.}},\quad \dots ,\quad \mathrm {J} _{k}={\text{const.}},$

que nous nous donnons arbitrairement. En d’autres termes, parmi tous les systèmes qui satisfont aux $h$ conditions (11), nous considérons seulement ceux qui satisfont en même temps aux $k-h$ conditions (12). Et $\rho '\,d\sigma$ sera proportionnel à la probabilité pour qu’un système satisfaisant à la fois aux conditions (11) et (12) ait sa particule représentative Π située sur l’élément $d\sigma$ de la multiplicité à $2n-k$ dimensions définie par les conditions simultanées (11) et (12).

Remarque. — Dans les cas que nous considérerons, les multiplicités à $2n-k$ dimensions que nous aurons à envisager présenteront la symétrie de sphères concentriques ou de cylindres coaxiaux, si bien que la quantité $\zeta$ sera une constante tout le long de la multiplicité envisagée, et il en sera de même de $\rho '$.

80.Appliquons les considérations précédentes à un système mécanique formé par un très grand nombre $n$ de projectiles dont l’action mutuelle dépend seulement des masses et de la distance : ce système sera, si l’on veut, un gaz dont chaque molécule est assimilée à un projectile. Soient $x_{1},$ $x_{2},$ $x_{3}$ les coordonnées du premier projectile dont la masse sera désignée indifféremment par $m_{1},$ $m_{2},$ ou $m_{3}.$ Soient de même $x_{4},$ $x_{5},$ $x_{6}$ les coordonnées du second projectile dont la masse sera désignée indifféremment par $m_{4},$ $m_{5},$ ou $m_{6}\dots$ Et ainsi de suite.

Nous poserons

$q_{i}={\sqrt {m_{i}}}x_{i}$

et

$p_{i}={\sqrt {m_{i}}}{\frac {dx_{i}}{dt}}={\sqrt {m_{i}}}x'_{i}$

L’énergie potentielle $\mathrm {U}$ du système sera une certaine fonction des $x_{i},$ c’est-à-dire des $q_{i}.$ La demi-force vive $\mathrm {T}$ aura pour valeur

$\mathrm {T} ={\frac {1}{2}}\sum m_{i}x_{i}'^{2}={\frac {1}{2}}\sum q_{i}'^{2}={\frac {1}{2}}\sum p_{i}^{2}.$

Et comme on a

$p_{i}={\frac {d\mathrm {T} }{dq_{i}'}},$

les $q_{i}$ et les $p_{i}$ forment un système de variables canoniques ; autrement dit, on aura pour définir le mouvement les équations de Hamilton

(8)

${\begin{aligned}{\frac {dq_{i}}{dt}}&={\frac {d\mathrm {E} }{dp_{i}}},&{\frac {dp_{i}}{dt}}&=-{\frac {d\mathrm {E} }{dq_{i}}},\end{aligned}}$

où $\mathrm {E} =\mathrm {T+U}$ représente l’énergie totale.

En supposant que les positions des molécules ou projectiles soient données, les $q_{i}$ et $\mathrm {U}$ seront des constantes fixées une fois pour toutes. Cherchons alors une loi de probabilité pour les vitesses, c’est-à-dire pour les $p_{i}$. En d’autres termes, cherchons comment les vitesses seront distribuées en moyenne chaque fois que le système repassera par sa configuration initiale (ou par une configuration très voisine).

On conçoit que les considérations développées plus haut trouvent ici leur application. Supposons d’abord que les équations (8) n’admettent pas d’autre intégrale que celle des forces vives

$\mathrm {E} ={\text{const.}}$

Dans l’espace à $2n$ dimensions des coordonnées $q_{i}$ et $p_{i}$, nous aurons alors à considérer la multiplicité à $2n-1$ dimensions

(13)

$\mathrm {E} ={\text{const.}}$

Mais comme on nous a imposé d’avance les positions de toutes les molécules, c’est-à-dire les $q_{i},$ il faudra que nous prenions l’intersection de cette multiplicité avec les plans

$q_{1}={\text{const.}},\quad q_{2}={\text{const.}},\quad \dots ,\quad q_{n}={\text{const.}}$

Cette intersection est une multiplicité M à $n-1$ dimensions. Les $q_{i}$ et $\mathrm {U}$ étant des constantes, l’équation (13) s’écrit simplement

$\mathrm {T} ={\frac {1}{2}}\sum p_{i}^{2}={\text{const.}}\,;$

telle est, dans l’espace à n dimensions des $p_{i},$ l’équation de notre multiplicité M à $n-1$ dimensions.

Cette multiplicité M présente, on le voit, la symétrie d’une sphère ; par suite (d’après la remarque faite à la page 104) la quantité appelée plus haut $\zeta$ et la densité fictive $\rho '$ sont constantes tout le long de cette multiplicité M, que nous pouvons appeler une sphère à $n-1$ dimensions, pour faciliter le langage.

Le point

$p_{1},\,p_{2},\,\dots \,\,p_{n}$

représentatif des vitesses de notre système est donc situé sur cette sphère. Et comme la densité $\rho '$ à la surface de cette sphère est constante, nous pouvons dire que la probabilité, pour que ce point représentatif soit situé dans une certaine région R de cette sphère, est proportionnelle à la surface de cette région R.

Quelle est alors la probabilité pour que $p_{1}$ soit compris entre $p_{1}^{0}$ et $p_{1}^{0}+dp_{1}^{0}$ ? Nous n’aurons qu’à prendre comme région R la zone découpée sur la sphère par les deux plans

$p_{1}=p_{1}^{0},\qquad \,p_{1}=p_{1}^{0}+dp_{1}^{0}\,;$

et la probabilité cherchée sera proportionnelle à la surface de cette zone, surface que nous allons évaluer. Appelons $r$ le rayon de notre sphère à $n-1$ dimensions. Ce rayon est défini par

$\sum p_{i}^{2}=r^{2}\,;$

et nous posons

$r^{2}=nk^{2},$

$n$ étant le nombre des molécules ; la constante $k^{2}$ sera alors la moyenne arithmétique de tous les $p_{i}^{2}$. Si nous posons

$p_{1}^{0}=r\cos \theta ,$

la surface de la zone en question sera proportionnelle à

$\sin ^{n-2}\theta \,d\theta ,$

c’est-à-dire à

$\sin ^{n-3}\theta \,dp_{1}^{0}.$

Mais nous avons

${\begin{aligned}\sin ^{2}\theta &=1-{\frac {{p_{1}^{0}}^{2}}{r^{2}}},\\&=1-{\frac {{p_{1}^{0}}^{2}}{nk^{2}}}\,;\end{aligned}}$

par suite nous pouvons représenter la surface de notre zone par

$\mathrm {A} \left(1-{\frac {{p_{1}^{0}}^{2}}{nk^{2}}}\right)^{\frac {n-3}{2}}\,dp_{1}^{0}\,;$

cette expression représente aussi la probabilité pour que $p_{1}$ soit compris entre $p_{1}^{0}$ et $p_{1}^{0}+dp_{1}^{0}.$ Comme $n$ est très grand, par hypothèse, on peut écrire approximativement^[12]

$\left(1-{\frac {{p_{1}^{0}}^{2}}{nk^{2}}}\right)^{\frac {n-3}{2}}=e^{-{\frac {{p_{1}^{0}}^{2}}{2k^{2}}}},$

ce qui donne à la probabilité la forme

$\mathrm {A} \,e^{-{\frac {{p_{1}^{0}}^{2}}{2k^{2}}}}\,dp_{1}^{0}.$

Telle est l’expression de la loi de Maxwell sur la répartition des vitesses des molécules gazeuses^[13].

Le point

$p_{1},\,p_{2},\,\dots ,\,p_{n},$

étant situé sur la sphère

$\sum p_{i}^{2}=\,{\text{const.}},$

et la densité fictive $\rho '$ étant constante à la surface de cette sphère, tous les $p_{i}^{2}$ ont même valeur moyenne ; ce que nous écrivons

${\overline {p_{i}^{2}}}={\overline {p_{1}^{2}}},$

en surmontant les lettres d’un trait pour indiquer qu’il s’agit de valeurs moyennes. Faisant d’abord $i=2,$ $p_{1}$ et $p_{2}$ sont relatifs à une même molécule, et l’équation précédente montre que cette molécule a même force vive moyenne dans le sens des $x$ et dans le sens des $y.$ Si $p_{i}$ et $p_{1}$ sont relatifs tous deux à l’axe des $x,$ mais à deux molécules différentes, la même équation prouve que ces deux molécules ont, suivant une même direction, la même force vive moyenne. Donc, si l’une des molécules a une masse plus grande que celle de l’autre, sa vitesse moyenne sera plus faible.

81.La démonstration précédente s’applique au cas d’un gaz enfermé dans un vase à la même température que lui. Si le gaz est entièrement libre, cette démonstration demande à être complétée. Dans ce dernier cas, en effet, les équations (8) du mouvement n’admettent pas seulement l’intégrale des forces vives qui s’écrit toujours, les $q_{i}$ étant supposés donnés,

(14)

$\sum p_{i}^{2}={\text{const.}},$

elles admettent aussi les intégrales du centre de gravité^[14]. Si nous projetons la quantité de mouvement de toutes les molécules sur la direction quelconque dont $\varepsilon _{1},\,\varepsilon _{2},\,\varepsilon _{3}$ sont les cosinus directeurs, la somme de ces projections est une constante $\mathrm {A} .$ La première molécule a pour quantité de mouvement en projection sur cette direction

$\varepsilon _{1}m_{1}x'_{1}+\varepsilon _{2}m_{2}x'_{2}+\varepsilon _{3}m_{3}x'_{3}=\varepsilon _{1}{\sqrt {m_{1}}}p_{1}+\varepsilon _{2}{\sqrt {m_{2}}}p_{2}+\varepsilon _{3}{\sqrt {m_{3}}}p_{3}.$

La seconde molécule a de même pour projection de sa quantité de mouvement sur la même direction l’expression

$\varepsilon _{4}{\sqrt {m_{4}}}p_{4}+\varepsilon _{5}{\sqrt {m_{5}}}p_{5}+\varepsilon _{6}{\sqrt {m_{6}}}p_{6},$

où l’on a posé, pour plus de symétrie dans les notations,

${\begin{aligned}\varepsilon _{4}&=\varepsilon _{1},&\varepsilon _{5}&=\varepsilon _{2},&\varepsilon _{6}&=\varepsilon _{3}.\end{aligned}}$

Et ainsi de suite. L’intégrale du mouvement du centre de gravité, en projection sur la direction envisagée, s’écrit donc

(15)

$\sum \varepsilon _{i}{\sqrt {m_{i}}}p_{i}=\mathrm {A} \,;$

dans cette égalité on a posé

${\begin{alignedat}{5}\varepsilon _{1}&{}=\varepsilon _{4}&{}={}&\varepsilon _{7}&{}={}&\dots &{}={}&\varepsilon _{3\nu -2}&{}={}&\dots ,\\\varepsilon _{2}&{}=\varepsilon _{5}&{}={}&\varepsilon _{8}&{}={}&\dots &{}={}&\varepsilon _{3\nu -1}&{}={}&\dots ,\\\varepsilon _{3}&{}=\varepsilon _{6}&{}={}&\varepsilon _{9}&{}={}&\dots &{}={}&\varepsilon _{3\nu }&{}={}&\dots .\end{alignedat}}$

Nous devons, dans l’espace à $n$ dimensions, couper la sphère (14) par le plan (15) : l’intersection est une sphère à $n-2$ dimensions dont nous appelons $p_{i}^{0}$ les coordonnées du centre. Pour avoir ce centre, nous abaissons de l’origine la perpendiculaire sur le plan (15) ; nous obtenons les équations

$p_{i}^{0}=\varepsilon _{i}{\sqrt {m_{i}}}k,$

qui expriment que les $p_{i}^{0}$ sont proportionnels aux cosinus directeurs de la normale au plan (15) ; et pour déterminer la constante $k,$ nous écrivons que le point $p_{i}^{0}$ est situé dans le plan (15), ce qui donne

$k\sum \varepsilon _{i}^{2}m_{i}=\mathrm {A} .$

Ayant ainsi obtenu le centre de notre sphère à $n-2$ dimensions, transportons-y l’origine en posant

$p_{i}=p'_{i}+p_{i}^{0}.$

La sphère (14) devient alors

$\sum {p'_{i}}^{2}+2\sum p'_{i}p_{i}^{0}+\sum {p_{i}^{0}}^{2}={\text{const.}}$

or, on a

${\begin{aligned}\sum p'_{i}p_{i}^{0}&=k\sum \varepsilon _{i}{\sqrt {m_{i}}}p'_{i}\\[0.5ex]&=k\left[\sum \varepsilon _{i}{\sqrt {m_{i}}}p_{i}-\sum \varepsilon _{i}{\sqrt {m_{i}}}p_{i}^{0}\right]\\[0.5ex]&=k\left[\mathrm {A} -\mathrm {A} \right]\\[0.5ex]&=0\,;\end{aligned}}$

par suite, l’équation de la sphère (14) s’écrit

$\sum {p'_{i}}^{2}={\text{const.}}$

Il faut couper cette sphère par le plan diamétral (15), devenu

$\sum \varepsilon _{i}{\sqrt {m_{i}}}p'_{i}=0.$

La multiplicité à $n-2$ dimensions qui résulte de cette intersection présente encore la symétrie de la sphère. Un raisonnement identique à celui qui a été fait plus haut montrerait alors que la distribution des $p'_{i}$ satisfait encore à la loi de Maxwell.

Or, si l’on fait successivement

${\begin{aligned}t_{1}&=1,&t_{2}&=0,&t_{3}&=0,\end{aligned}}$

puis

${\begin{aligned}t_{1}&=0,&t_{2}&=1,&t_{3}&=0,\end{aligned}}$

enfin

${\begin{aligned}t_{1}&=0,&t_{2}&=0,&t_{3}&=1,\end{aligned}}$

afin d’utiliser l’ensemble des trois intégrales du centre de gravité, les $p_{i}'$ ne sont autre chose, on le voit aisément, que les variables qui correspondent aux vitesses des molécules par rapport au centre de gravité du système.

Nous pouvons donc dire que dans une masse gazeuse entièrement libre, la distribution des vitesses relatives par rapport au centre de gravité satisfait encore à la loi de Maxwell. En particulier, les diverses molécules auront même force vive moyenne ; si leurs masses sont inégales, les grosses molécules auront, relativement au centre de gravité, une vitesse moyenne plus faible que les petites ; plus les masses des molécules seront grandes, plus leurs vitesses se rapprocheront de celle du centre de gravité.

82.Tout ce qui précède s’applique aux gaz, arrivés à un état stationnaire, et qui, par conséquent, se trouvent dans leur ensemble en état d’équilibre mécanique et thermique. Lorsqu’au contraire la masse gazeuse possède diverses régions où les vitesses et les températures ne sont pas les mêmes, le mécanisme du frottement et de la conductibilité tend à égaliser ces vitesses et ces températures, et à déterminer un état stationnaire. Considérons, en effet, deux portions contiguës A et B où les vitesses moyennes sont différentes, les molécules de B, par exemple, présentant une prépondérance de vitesses dirigées dans un certain sens. Des échanges de molécules s’effectuent entre les régions A et B, et les molécules qui passent de B en A apportent avec elles leur vitesse ; la prépondérance diminuera donc en B et la vitesse augmentera en A : c’est ainsi que le frottement ou la viscosité de la masse gazeuse tend à égaliser les vitesses de A et de B, et à rendre nulle la vitesse relative de l’une des régions par rapport à l’autre. L’ensemble de la masse gazeuse tendra donc vers un état final où elle se mouvra d’un bloc, à la façon d’un corps solide. Si le moment de rotation total était nul initialement, cet état final est une simple translation ; si ce moment de rotation initial existait, l’état final est une translation accompagnée d’une rotation autour d’un certain axe.

Le mécanisme de la conductibilité thermique est entièrement analogue. Reprenons nos deux régions contiguës A et B et supposons la région B plus chaude que la région A. Les molécules de B auront alors une force vive moyenne supérieure à celle des molécules de A ; par suite les molécules qui passent de B en A tendent à échauffer A ; celles qui passent de A en B tendent à refroidir B. Les températures finiront donc par s’égaliser.

Toutefois, si la masse gazeuse est d’un volume considérable, elle n’arrivera à son état final stationnaire tant mécanique que thermique, qu’au bout d’un temps excessivement long^[15]. Mais chaque petit volume atteindra assez rapidement un état d’équilibre local, où les vitesses des molécules satisferont à la loi de Maxwell (il s’agit ici des vitesses relatives par rapport au centre de gravité de la région restreinte envisagée).

83.Revenons maintenant à la nébuleuse chaotique de M. du Ligondès, et voyons dans quelle mesure tout ce qui vient d’être dit sur les vitesses des molécules gazeuses dans la théorie cinétique s’applique aux projectiles qui composent cette nébuleuse. Si ces projectiles étaient parfaitement élastiques, l’assimilation serait complète. Lorsque deux projectiles élastiques de même masse, qui se sont choqués,
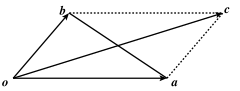
fig.18. rebondissent l’un sur l’autre, la vitesse de leur centre de gravité commun n’a pas changé, la force vive totale non plus ; quant à la vitesse relative de l’un par rapport à l’autre, elle n’a pas changé en grandeur, mais elle a changé en direction. En d’autres termes, si les vecteurs $oa$ et $ob$ représentent (fig. 18) les quantités de mouvement des deux projectiles avant le choc, leur somme géométrique $oc$ n’a pas changé ; leur différence géométrique $ab$ a conservé sa grandeur mais a varié en direction. Telles sont les lois du choc de deux corps élastiques de même masse.

Considérons maintenant deux points matériels A et B de même masse s’attirant (on se repoussant) suivant une loi quelconque fonction de la distance, l’action étant nulle à distance infinie. Quand ces deux points sont très éloignés l’un de l’autre, leurs trajectoires sont rectilignes ; elles s’incurvent (fig. 19) lorsque ces deux points viennent à passer l’un près de l’autre ; puis, la distance augmentant, les deux trajectoires redeviennent rectilignes. La force vive n’a pas changé ; quant à la vitesse relative, lorsque les deux points sont arrivés en A′ et en B′ où les trajectoires sont redevenues sensiblement rectilignes, elle
fig.19. n’a pas varié en grandeur, mois elle a changé en direction. Nous retrouvons donc exactement les mêmes lois que dans le choc de deux corps élastiques ; en effet, le choc de deux corps élastiques peut être regardé comme un cas particulier du problème que nous envisageons. Nous conviendrons de dire que les points matériels A et B, ainsi déviés de leur route, ont subi un demi-choc. Les demi-chocs se font conformément aux lois des corps élastiques.

Les matériaux qui constituent la nébuleuse de M. du Ligondès et qui s’attirent entre eux suivant la loi newtonienne vont ainsi subir un grand nombre de demi-chocs : à ce point de vue ils sont assimilables aux molécules d’une masse gazeuse. Mais, à côté des demi-chocs, il faut distinguer aussi les chocs véritables qui ont lieu lorsque deux projectiles A et B viennent à se toucher physiquement. Ces chocs véritables se font toujours avec perte de force vive, et par suite avec tendance à la concentration, parce que les matériaux cosmiques ne sont pas parfaitement élastiques mais plutôt mous.

Les demi-chocs, dans la nébuleuse, sont certainement beaucoup plus fréquents que les chocs véritables. Par suite, malgré la possibilité de ceux-ci, les vitesses auront tout d’abord une tendance à se répartir selon la loi de Maxwell, les projectiles les plus gros prenant une vitesse moindre que les plus petits. L’effet concentrateur des chocs véritables produira quelques grosses agglomérations. Ces grosses agglomérations, en vertu de la loi de Maxwell (que les demi-chocs tendent toujours à maintenir), prendront une vitesse relative assez faible par rapport au centre de gravité de la région où chacune d’elles se trouve. Comme la nébuleuse entière, assimilée à une masse gazeuse, tend, par suite du frottement, à tourner d’un seul bloc comme le ferait un corps solide, les grosses agglomérations tendront finalement à prendre une vitesse peu différente de celle qui correspond à une rotation uniforme autour d’un axe.

Dans ces conditions, reconnaissons que les inclinaisons des orbites des grosses agglomérations sur le plan équatorial vont tendre à diminuer. Soient O le centre de la nébuleuse, Π le plan équatorial du maximum des aires et V la vitesse actuelle d’une grosse agglomération P (fig. 20). Cette vitesse tend à se rapprocher de la vitesse V′ qui
fig.20. correspondrait à une rotation uniforme autour d’un axe O$z$ perpendiculaire ou plan Π. Or il est manifeste que le plan OPV′ est moins incliné sur le plan Π que le plan OPV. Il y a donc à chaque instant tendance à la diminution de l’inclinaison de l’orbite de P, qui finira par se rapprocher du plan Π.

En même temps, l’excentricité de l’orbite tendra à diminuer. En effet, si PV est la vitesse de la grosse agglomération P en projection sur le plan équatorial (fig. 21), cette vitesse tend à se rapprocher de
fig.21. la vitesse PV′ qui est perpendiculaire au rayon vecteur et qui correspond à la rotation uniforme. L’orbite ayant une fois atteint la forme circulaire, la conservera comme il a été expliqué au Chapitre précédent.

On comprend également, et pour la même raison, pourquoi les orbites des planètes sont toutes directes^[16].

84.Il y a lieu ici de faire une remarque. Si les demi-chocs existaient seuls, comme ils se font conformément aux lois des corps élastiques, la nébuleuse chaotique serait alors entièrement assimilable à une masse gazeuse isolée dont la figure d’équilibre finale serait un sphéroïde très peu aplati et sans forte condensation centrale. Dans l’aplatissement et la concentration de la nébuleuse de M. du Ligondès, le rôle tout à fait essentiel est joué par les chocs véritables. Or, ceux-ci, nous l’avons dit, sont beaucoup moins fréquents que les demi-chocs. Sont-ils néanmoins assez nombreux pour qu’on puisse leur attribuer la transformation de la nébuleuse en système solaire, et n’est-il pas à craindre, au contraire, que l’effet des demi-chocs ne l’emporte ? La question n’est pas tranchée et demanderait à être approfondie.

85.Cherchons maintenant pourquoi les planètes ont un mouvement de rotation direct, excepté celles qui sont les plus éloignées du Soleil. Nous pourrions encore faire intervenir l’influence des marées solaires, telle que nous l’avons expliquée au Chapitre III, Section VI.

Ce n’est pas ce que fait M. du Ligondès. L’intensité de la pesanteur à l’intérieur de la nébuleuse ayant varié avec le temps, depuis l’origine où elle était proportionnelle à la distance au centre jusqu’à l’état final actuel où elle varie en raison inverse du carré de la distance, il admet, comme Faye (Cf. n^o 60, p. 72), qu’il y a eu à chaque distance une période directe et une période rétrograde. La loi par laquelle il représente l’intensité de la pesanteur dans la période intermédiaire est seulement plus compliquée, mais aussi elle est plus voisine de la réalité que celle de Faye. La période directe a duré très peu de temps pour les régions extérieures de Neptune et d’Uranus, aussi ces planètes sont-elles rétrogrades. Elle a duré beaucoup plus longtemps pour les régions des planètes intérieures, et lorsque la période rétrograde est arrivée en ces régions, il était trop tard pour changer le sens de rotation de ces planètes déjà presque complètement formées.

86.M. du Ligondès tente aussi d’expliquer certains faits particuliers offerts par le système solaire. Par exemple, Jupiter se trouve être la plus grosse des planètes, parce que le disque équatorial aplati, générateur des planètes, aurait présenté à la distance correspondant à Jupiter un maximum de densité. Il trouve aussi certaines raisons pour rendre compte des lois suivant lesquelles varient les masses des différentes planètes, leurs distances au Soleil, les inclinaisons de leurs axes.

Disons enfin que, d’après M. du Ligondès, l’ordre des planètes, rangées au point de vue de leur âge, serait le suivant : Jupiter, Neptune, Uranus, Saturne, la Terre, Mars, Vénus, Mercure.

Les considérations développées dans les n^os 85 et 86 nous paraissent avoir moins d’importance que les précédentes. On pourrait les abandonner sans renoncer aux principes fondamentaux de la théorie que nous venons d’exposer. En ce qui concerne le sens de la rotation des planètes, nous avons vu que la théorie des Marées était seule capable d’en rendre compte ; les objections faites aux idées de Faye sur la « période directe » et la « période rétrograde » conserveraient ici leur valeur. D’autre part, il nous semble prématuré de chercher à rendre compte, par des considérations a priori, des lois qui lient les masses des planètes aux grands axes de leurs orbites, à la durée de leur rotation, au nombre et à la répartition de leurs satellites. Si ces considérations étaient justifiées elles devraient s’appliquer aux systèmes planétaires qui entourent toutes les étoiles, et tous ces systèmes devraient être identiques ce qui est bien peu vraisemblable.

1. Lieutenant-Colonel M. du Ligondès : Formation mécanique du système du Monde (Paris, Gauthier-Villars, 1897).
2. L’unité astronomique est la distance moyenne de la Terre au Soleil. Les étoiles les plus voisines du Soleil en sont à une distance de l’ordre de 200 000 unités astronomiques.
3. Ce rapport dépend évidemment du rayon $\mathrm {R}$ que l’on assigne à la nébuleuse initiale, et ce rayon peut être choisi arbitrairement. Si, par exemple, au lieu de prendre $\mathrm {R} =$ 100 000 unités, nous avions pris $\mathrm {R} =$ 30 unités, c’est-à-dire le rayon de l’orbite de Neptune, nous aurions trouvé ${\frac {\mathrm {S} _{g}}{\mathrm {S} _{a}}}$ de l’ordre de 1/500. Contentons-nous de remarquer que ce rapport est toujours petit.
4. 250 fois environ pour la 61^e du Cygne, et plus de 2 000 fois pour α du Centaure.
5. Les axes de coordonnées sont les axes principaux de l’ellipsoïde ; $\alpha ^{2},$ $\beta ^{2},$ $\gamma ^{2}$ sont les trois constantes que nous avons appelées $\mathrm {P} ,$ $\mathrm {Q} ,$ $\mathrm {R}$ au Chap. III, Section VII (p. 55).
6. Nous avons déjà signalé ce point, à propos de l’hypothèse de Kant (Ch. I, n^o 1, p. 2).
7. Si, passant à une seconde approximation, on tenait compte, avec van der Waals, des dimensions finies des sphères d’action des molécules, on trouverait, au lieu de la formule de Mariotte et Gay-Lussac sur laquelle nous tombons plus loin, une formule plus approchée. Nous n’en avons pas besoin ici.
8. Remarquons de plus ce fait curieux : l’énergie cinétique moyenne $\mathrm {T}$ va aussi en augmentant ; les chocs ont pour effet d’augmenter les vitesses. Ce fait est à comparer au suivant que nous rencontrerons au Chapitre prochain : une résistance de milieu a pour effet d’accroître la vitesse linéaire d’une planète ou d’une comète. Nous aurons aussi plus loin (Ch. VIII, n^o 168) l’occasion de constater un autre paradoxe du même genre.
9. $\rho$ sera le rapport du nombre des molécules roses au nombre total des molécules comprises dans un petit volume entourant le point $x,\,y,\,z.$
10. C’est ce qui arrive, par exemple, pour une courbe de Lissajous analogue à celles que nous avons considérées au n^o 71 (p. 87), et qui emplit tout un parallélépipède si les trois constantes $\alpha ,$ $\beta ,$ $\gamma$ du n^o 71 ne sont pas commensurables entre elles.
11. La densité $\rho$ est proportionnelle au nombre de particules Π intérieures à l’unité de volume, au voisinage du point considéré.
12. On sait en effet que $\left(1+{\frac {x}{n}}\right)^{n}$ a pour limite $\mathrm {e} ^{x}$ quand n croît indéfiniment.
13. Si, parmi les $n$ molécules, il s’en trouve deux identiques, on peut les intervertir sans changer la configuration du système ; les deux systèmes ainsi définis satisfont à la même loi de probabilité. S’il se trouve N molécules identiques, on peut les intervertir de N ! façons différentes : on obtient ainsi N ! systèmes satisfaisant à la même loi de probabilité. Cette loi subsiste donc même si l’on ne considère pas comme distincts ces N ! systèmes qui offrent tous la même configuration.
14. Ces intégrales n’existaient pas dans le cas d’un gaz renfermé dans un vase, puisque les molécules étaient soumises aux réactions des parois du vase qui sont des forces extérieures au système.
15. Voir ce qui a été dit au Chap. III, Section IV, au sujet de la faiblesse de l’influence des frottements quand il s’agit de grands volumes fluides.
16. Observons que, dans l’hypothèse de M. du Ligondès, il n’est pas nécessaire de supposer que la différentiation initiale de la nébuleuse s’est faite sous forme d’anneaux : les grosses agglomérations ont pu se produire d’une façon quelconque à son intérieur.