Leçons sur les hypothèses cosmogoniques (Poincaré, 1911)/Chapitre 03
CHAPITRE iii.
ANALYSE DE L’HYPOTHÈSE DE LAPLACE. TRAVAUX DE ROCHE. ÉTUDE DE LA STABILITÉ D’UN ANNEAU. FORMATION DES SATELLITES.
I. — Surfaces de niveau.
14.Nous allons maintenant entrer dans le détail de l’hypothèse de Laplace, et, comme l’a fait Roche[1], soumettre cette hypothèse au calcul.
Considérons la nébuleuse de Laplace, constituée, nous l’avons dit, par un noyau central condensé, entouré d’une atmosphère très ténue, dont la masse est supposée très petite par rapport à celle de la condensation centrale. Les couches atmosphériques sont supposées participer, en vertu des frottements, à la rotation du noyau qu’elles recouvrent, de sorte que l’ensemble est animé d’une vitesse angulaire uniforme . Désignons par la masse du noyau que nous supposons sphérique, et négligeons l’attraction mutuelle des molécules de l’atmosphère. Quelle sera, dans ces conditions, la forme des surfaces de niveau ?
Prenons pour axe des l’axe de rotation de la nébuleuse, pour plan des le plan perpendiculaire à l’axe de rotation mené par le centre de gravité O ; et désignons par
la distance d’un point quelconque à l’origine.
Le potentiel dû à l’attraction du noyau central est
le potentiel dû à la force centrifuge est
L’équation générale des surfaces de niveau (surfaces équipotentielles) s’écrira donc
désignant une constante. Les surfaces de niveau sont donc, comme il était évident a priori, de révolution autour de ox et symétriques par rapport au plan yoz. Nous obtiendrons l’équation des méridiennes de ces surfaces en faisant dans l’équation précédente, ce qui donne
| (1) |
Lorsque la constante est très grande, chaque méridienne (fig. 2)
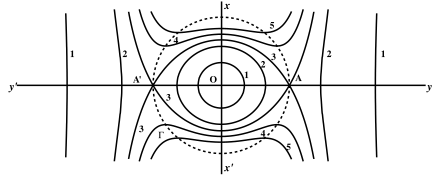
fig.2.
se compose d’une petite courbe entourant l’origine et de deux branches
infinies très éloignées, coupant l’axe des l’ensemble de la méridienne est désigné par 1 dans la figure. Lorsque diminue, la courbe
entourant l’origine se dilate, les deux branches infinies se rapprochent,
et donnent l’ensemble de courbes 2. Si la constante diminue encore,
on obtient la courbe 3 qui présente deux points doubles sur l’axe ,
puis enfin des courbes telles que 4 et 5 qui ne coupent plus l’axe
des
15.Quels seront les points de ces courbes où la tangente sera parallèle à ? On obtiendra ces points en différentiant par rapport à l’équation (1) de ces courbes, ce qui donne
Cette équation est satisfaite pour les points de l’axe des x sont, en effet, des sommets pour nos courbes ; elle est satisfaite également pour
le lieu des points où la tangente sera parallèle à est donc (en dehors de l’axe des ) un cercle de rayon
En chaque point de ce cercle, on a
c’est-à-dire que la force centrifuge est égale et opposée à la composante de la gravité parallèle à En particulier, aux deux points doubles A et A’, la force centrifuge balance exactement la pesanteur.
16.Cela posé, reprenons notre nébuleuse qui tourne tout d’une pièce. Son atmosphère, qui est supposée s’étendre aussi loin que possible, se termine nécessairement à la plus grande des surfaces de niveau dont la méridienne ne dépasse pas le cercle , car, au delà de ce cercle la force centrifuge l’emporterait sur la pesanteur. La surface libre de l’atmosphère est donc engendrée par la révolution de la courbe à points doubles 3 autour de : cette surface présente une arête saillante tout le long de l’équateur. La surface de niveau qui vient immédiatement après n’enveloppe pas complètement les précédentes : elle s’ouvre à l’équateur, puis se développe en deux nappes infinies, comme le montre la figure 2.
Lorsque la nébuleuse se contractera par suite du refroidissement, la vitesse de rotation augmentera, d’après la loi des aires ; le rayon du cercle défini par
diminuera : la surface libre de l’atmosphère se contractera donc, pour ainsi dire, en restant semblable à elle-même. Par suite de cette contraction, la couche fluide qui se trouve en excès descend des pôles vers l’équateur en coulant le long des surfaces de niveau, puis elle s’échappe, comme par une ouverture, par l’arête saillante que nous avons signalée. Elle cesse dès lors de faire partie de l’atmosphère de la nébuleuse : elle forme une zone équatoriale dont les particules continueront à décrire des cercles autour du centre, dans le plan de l’équateur, puisqu’au moment de l’abandon la force centrifuge faisait équilibre à la pesanteur.
Nous comprenons donc maintenant la formation des anneaux de Laplace : elle est due à la présence, sur la méridienne de la surface libre, des deux points doubles A et A’, dont l’importance a été mise en évidence par Roche[2].
II. — Nécessité de l’hypothèse d’une condensation centrale.
17.Dans ce qui précède, nous avons, avec Laplace, supposé une très forte condensation centrale de notre nébuleuse. Aurions-nous pu nous dispenser de cette hypothèse ? Il est facile de voir que non.
Reprenons en effet, en abandonnant cette hypothèse, la détermination de nos surfaces de niveau. Le potentiel dû à la force centrifuge est toujours
Appelant le potentiel dû à l’attraction, nous aurons pour le potentiel total
L’équation des surfaces de niveau sera
et l’équation de leurs méridiennes, dans le plan des sera
Pourrons-nous avoir, pour la surface libre de l’atmosphère une arête saillante, par où la condensation laissera s’échapper des molécules pour former un anneau ? Oui, s’il existe une méridienne présentant des points doubles, ce qui arrivera en général, car les trois équations
détermineront un point double situé sur l’axe des y. En effet, sur cet axe, on a
par raison de symétrie : les deux autres équations déterminent les valeurs de et de
Nous aurons donc bien une méridienne à point double, et de plus, comme nous l’apprend l’équation
en ce point double la force totale, résultante de la gravité et de la force centrifuge, sera nulle.
Donc il y aura, comme précédemment, abandon de molécules dans
le plan de l’équateur. Ces molécules commenceront par décrire des
cercles autour de la nébuleuse qu’elles viennent d’abandonner, puisqu’au moment de l’abandon la force centrifuge contrebalance la
pesanteur. On pourrait croire, à première vue que rien n’est changé et
que l’anneau ainsi formé continuera à se comporter comme un anneau
de Laplace. Il n’en est rien. Représentons, en effet, un anneau AA′
(fig. 3) qui vient de se détacher de la nébuleuse. Ses molécules décrivent des cercles autour de l’axe sous l’action d’une attraction
égale à la force centrifuge. Lorsque le refroidissement aura contracté
la nébuleuse, la force centrifuge sera bien toujours la même, mais
l’attraction, qui est celle d’un corps aplati, aura varié, (tandis que,
dans l’hypothèse de Laplace, l’attraction du noyau sphérique ne variait pas avec la condensation). Il semble donc que les orbites des
molécules ne pourront pas rester circulaires, et qu’elles deviendront
excentriques. Mais nous verrons plus loin, à propos de la théorie de Faye, qu’une planète décrivant une orbite primitivement circulaire et
soumise à une attraction lentement variable d’après une loi quelconque,
conservera une orbite circulaire.

fig.3.
18.On peut encore mettre en évidence la nécessité de supposer une grande condensation à la nébuleuse de Laplace, par les calculs suivants dus à M. Fouché[3]. Nous connaissons le moment de rotation du système solaire : il est approximativement égal au moment de rotation du Soleil autour de son axe, augmenté du moment dû à la révolution de l’ensemble des planètes autour du Soleil, (le moment dû à la rotation de chaque planète autour de son axe étant négligeable). Prenant pour unités le rayon de l’orbite terrestre, la masse du Soleil et le jour moyen, M. Fouché donne les chiffres suivants :
Pour le moment dû à la rotation du Soleil
Pour le moment dû à la révolution des planètes
on voit donc que la plus grande partie du moment de rotation est dû aux planètes, et que le moment de rotation total est égal à
D’après le théorème des aires, ce moment n’a pas dû varier depuis l’origine. Supposons un instant qu’à l’époque où la nébuleuse a abandonné l’anneau qui a formé Neptune, cette nébuleuse était homogène. Son moment de rotation eût été alors comparable à celui d’une sphère homogène, de même masse que le Soleil, s’étendant jusqu’à l’orbite de Neptune et tournant avec la vitesse angulaire actuelle de cette planète. Ce moment de rotation égale
chiffre plus de six cents fois plus grand que le précédent. On voit donc quelle énorme condensation il faut accepter pour réduire le moment de rotation à la six-centième partie de ce qu’il serait dans le cas d’homogénéité,
M. Fouché présente encore la chose d’autre manière. Imaginons, pour prendre un cas simple, la nébuleuse formée d’un noyau sphérique, entouré d’une atmosphère homogène s’étendant jusqu’à l’orbite de Neptune, le tout tournant avec la vitesse angulaire actuelle de cette planète. Le théorème des aires exige que la somme du moment de rotation du noyau et du moment de rotation de l’atmosphère soit égale a
par conséquent le moment de rotation de l’atmosphère est inférieur à
Or, si nous appelons la masse de cette atmosphère, son moment de rotation est comparable à celui d’une sphère homogène de masse , c’est-à-dire à
ce moment devant être inférieur au précédent, il vient
chiffre à peine supérieur à la masse de toutes les planètes réunies. Il faudrait donc que l’atmosphère tout entière de la nébuleuse se fût réduite en planètes, si cette atmosphère avait été homogène.
Les calculs précédents ne sont relatifs qu’à des ordres de grandeur ; mais ils suffisent pour montrer combien est capital, dans la théorie de Laplace, le fait de la condensation centrale.
19.Sans cette condensation, il aurait fallu, dans le calcul des surfaces de niveau, tenir compte de l’attraction des molécules de l’atmosphère les unes sur les autres, ce qui nous aurait donné, pour leurs
méridiennes, des courbes analogues à celles de la figure 4. L’anneau

fig.4.
abandonné aurait eu un profil tel que ACD. Nous allons trouver facilement une limite inférieure à la densité d’un tel anneau. Appliquons
au volume total de l’anneau, c’est-à-dire au volume engendré par la
révolution de ACD autour de , la formule bien connue de Green
où représente un élément du volume, un élément de la surface qui limite ce volume, la dérivée normale intérieure et le potentiel total
dont il a été question plus haut. La stabilité exige qu’à la surface ACD de l’anneau, la force totale soit dirigée vers l’intérieur, c’est-à-dire que
ce qui donne par conséquent
| (2) |
Or, si est la densité de l’anneau, nous avons, d’après la formule de Poisson,
d’ailleurs
par suite
Si nous admettons, pour simplifier, que la densité est uniforme dans tout l’anneau (ou plus généralement, si nous désignons par la densité moyenne de l’anneau), l’inégalité (2) exige que
d’où
nous avons ainsi une limite inférieure de la densité de l’anneau, et a fortiori de la nébuleuse. Lorsqu’on prend pour la vitesse angulaire de Neptune, on trouve pour un chiffre tellement grand que, d’après ce chiffre, la masse totale de la nébuleuse serait très supérieure à celle du Soleil.
III. — Formation successive des anneaux.
20.Revenons à l’hypothèse de Laplace d’une très forte condensation centrale, hypothèse où nous négligeons l’action mutuelle des molécules de l’atmosphère. L’équation des surfaces de niveau est alors, nous l’avons vu dans la Section I,
ces surfaces ont leurs méridiennes représentées sur la figure 2.
Si, dans cette équation, nous changeons
cette équation ne change pas, et la figure 2 est simplement remplacée par son homothétique, le rapport d’homothétie étant c’est un cas de similitude mécanique.
Dans ces conditions,
| le volume | se trouve multiplié par |
| le moment d'inertie | se trouve multiplié par |
| le moment de rotation | se trouve multiplié par |
les deux expressions
ne changent pas. C’est dire que la forme des surfaces de niveau ne dépend que de
si l’on adopte comme variables définissant la nébuleuse et elle ne dépend que de
si l’on adopte comme variables et . À la surface lenticulaire à arête saillante (engendrée par la révolution de la méridienne à points doubles), correspondront toujours pour ces expressions deux valeurs bien déterminées et . Toutes les fois donc que nous aurons
nous dépasserons cette surface lenticulaire et la surface libre s’ouvrira à l’équateur. Nous aurons donc abandon de molécules et formation d’un anneau de Laplace.
21.Que se passera-t-il par suite du refroidissement de notre nébuleuse ? La masse du noyau et le moment de rotation resteront constants, tandis que diminuera ; donc
augmentera et dépassera la limite : il se formera un anneau. Si le refroidissement restait uniforme, ce processus serait continu, et nous aurions une plage continue de vapeurs abandonnées dans tout le plan de l’équateur, et non pas une série discrète d’anneaux séparés les uns des autres.
Pour expliquer la formation successive des anneaux, il faut donc supposer, avec Roche, que le refroidissement n’est pas uniforme. Supposons d’abord le refroidissement purement superficiel. diminuera, mais ne variera pas sensiblement, le moment d’inertie n’ayant guère changé, car la densité de l’atmosphère est très faible. Quant à il reste toujours constant. Donc
diminuant, il ne se formera pas d’anneau. Si, au contraire, le refroidissement est central, demeurera constant, tandis que ira en croissant par suite de la condensation du noyau qui diminue le moment d’inertie. Donc
ira en augmentant, dépassera la limite , et il y aura production d’un anneau.
Mais un refroidissement central ne sera pas suivi immédiatement de la formation d’un anneau. En effet, par suite d’une condensation centrale, la vitesse de rotation du noyau augmentera, celle de la partie superficielle demeurant la même au moins pendant un certain temps, car il faut un certain temps pour que le frottement parvienne à communiquer à la périphérie la vitesse angulaire que possède le noyau. Or, la vitesse angulaire , qui importe pour la formation d’un anneau, c’est celle de la superficie. Pendant un certain intervalle de temps, et restent donc constants, et il ne se forme pas d’anneau.
22.Comment expliquer ces alternances de refroidissement central
et de refroidissement superficiel ? Supposons que notre nébuleuse ait

fig.5.
atteint la forme lenticulaire ABA′B′ (fig. 5), puis, qu’elle se contracte et arrive à la nouvelle forme lenticulaire A1B1A′1B′1 : il se produit alors un anneau équatorial. En même temps une portion de
fluide atmosphérique en excès descend des pôles vers l’équateur,
mettant ainsi brusquement à nu une nouvelle couche A1B1A′1B′1,
qui va se refroidir rapidement. Donc l’instant de l’abandon d’un
anneau est immédiatement suivi d’une période de refroidissement
superficiel, pendant laquelle il ne se formera pas d’anneau. Cette période durera jusqu’à ce que, le refroidissement ayant gagné les parties
centrales, le même mécanisme puisse se renouveler. Nous comprenons ainsi que les anneaux aient pu se produire d’une manière
discontinue.
23.D’après la loi de Bode, la planète de rang se trouve à une distance du Soleil donnée par la formule
et étant deux constantes. Donc, au moment de l’abandon des anneaux successifs, le rayon équatorial de la nébuleuse solaire devait être représenté par cette formule. D’autre part, en vertu de la loi exponentielle du refroidissement, ce rayon, variable avec le temps , devait être représenté par une expression telle que
étant trois constantes. Par suite, l’époque de l’abandon de l’anneau de rang est donnée par l’équation
Or, attribuer à une suite de valeurs entières dans le premier membre de cette équation, revient à attribuer à , dans le second membre, des valeurs équidistantes. Donc les époques où la nébuleuse solaire a abandonné les anneaux successifs ont dû croître en progression arithmétique. Telle est, dans l’ordre d’idées qui nous occupe, la signification de la loi de Bode.
24.Revenons à notre nébuleuse qui abandonne un anneau en
passant, par contraction, de la forme lenticulaire ABA′B′ à la nouvelle forme lenticulaire A1B1A′1B′1 (fig. 5). Il y a lieu de remarquer
que, seules, les molécules qui se trouvaient déjà au voisinage de
l’équateur contribueront à former cet anneau, car les molécules de la portion de fluide atmosphérique en excès qui, des pôles descend vers
l’équateur en s’écoulant sur la surface libre, possédaient primitivement
une vitesse linéaire de circulation d’autant plus petite qu’elles étaient
plus voisines du pôle. Cette vitesse linéaire tendra à diminuer (en vertu
de la loi des aires) quand la molécule se rapprochera de l’équateur.
Les molécules qui affluent ainsi vers l’équateur ne possèdent donc
pas, en y arrivant, la vitesse nécessaire pour décrire un cercle, mais
une vitesse moindre. Chaque particule A partira donc tangentiellement
à l’équateur et décrira, dans le plan de cet équateur, une ellipse AA′
(fig. 6), de foyer O, d’autant plus excentrique que sa vitesse à l’aphélie A est plus faible. Les particules qui partent ainsi successivement de A n’ont pas toutes la même vitesse tangentielle ; mais toutes
celles qui sont animées d’une même vitesse tangentielle décrivent la
même ellipse et donnent une traînée elliptique intérieure à l’atmosphère de la nébuleuse. Il y a ainsi dans le plan de l’équateur des

fig.6.
traînées elliptiques, de toutes orientations et de grandeurs diverses,
qui se croisent entre elles. Les chocs résultant de la coexistence de
toutes ces traînées finiront bientôt par détruire les vitesses radiales et
par ne laisser subsister que la vitesse angulaire de circulation. L’ensemble des particules finira par constituer un système de cercles concentriques que Roche a appelé anneau intérieur, parce que ses particules se meuvent à l’intérieur de l’atmosphère et décrivent des cercles
dont le rayon est plus petit que celui de l’équateur.
Suivant les circonstances, un tel anneau intérieur pourra, ou bien subsister, si la résistance qu’oppose l’atmosphère au mouvement circulaire de ses particules est faible ; ou bien se détruire, si la résistance du milieu atmosphérique est assez forte pour faire tomber ses particules vers le centre. C’est principalement pour expliquer la formation de certains satellites que Roche a fait jouer un rôle aux anneaux intérieurs.
Remarquons que la formation des traînées elliptiques favorise les alternatives entre le refroidissement superficiel et le refroidissement central, des particules primitivement superficielles, et par suite froides, tombant vers le centre. Remarquons aussi qu’avec les anneaux intérieurs, Roche abandonne, au moins en partie, la conception primitive de Laplace, c’est-à-dire la conception d’une nébuleuse entièrement gazeuse. Si, en effet, un anneau intérieur était gazeux, il se mélangerait par diffusion au reste de l’atmosphère et ne pourrait jamais subsister. Il faut supposer que cet anneau est formé par des poussières météoriques tenues en suspension par le gaz de la nébuleuse.
IV. — Discussion de l’hypothèse d’une rotation uniforme.
25.La conception de Laplace repose sur le fait que la nébuleuse est animée d’une rotation uniforme, due au frottement des couches atmosphériques les unes sur les autres. C’est aussi le frottement qui, d’après Laplace, doit, dans les anneaux, augmenter la vitesse des molécules extérieures et diminuer celle des molécules intérieures, jusqu’à rendre uniforme la vitesse angulaire de l’anneau (fig. 1, p. 10).
Le frottement est-il vraiment capable de produire ces effets ? L’observation nous enseigne que, malgré les frottements, l’atmosphère du Soleil et les atmosphères des planètes ne possèdent pas une rotation uniforme. D’ailleurs, Helmholtz a montré combien, pour de grands volumes fluides, l’influence des frottements est longue à se faire sentir. Écrivons, en effet, les équations de l’hydrodynamique :
| (3) |
les trois premières sont les équations de Navier, la dernière est l’équation de continuité.
Dans ces équations désigne le potentiel des forces extérieures, la pression, la densité, le coefficient de viscosité, les composantes de la vitesse.
Si, dans les équations (3), nous multiplions
par une même constante , et que nous ne changions pas
ces équations ne changent pas.
Si donc nous considérons deux volumes fluides et homothétiques l’un de l’autre dans un rapport , et qu’aux points homologues nous ayons les mêmes valeurs initiales de
si, en outre, le coefficient de viscosité est fois plus grand pour le second volume que pour le premier, les phénomènes produits au bout du temps pour le premier volume se produiront pour le second au bout du temps . Le frottement agira donc plus lentement sur le second volume que sur le premier, bien que la viscosité du second volume soit plus forte.
Helmholtz a reconnu que, pour une atmosphère de 8 kilomètres d’épaisseur, le temps nécessaire pour réduire par le frottement de moitié une différence de vitesse est de 42 747 ans, soit 4.104. Ici l’épaisseur de notre atmosphère est le rayon de l’orbite de Neptune, soit 4.109 kilomètres ; le temps nécessaire pour réduire les différences de vitesse de moitié serait donc
années, avec un coefficient de viscosité plus grand que celui de notre atmosphère ; avec le même coefficient de viscosité, cela ferait
années. Il faut donc, si l’on veut que la rotation ait pu se maintenir sensiblement uniforme, que le processus de refroidissement et de production des anneaux ait été excessivement lent.
26.Cette faiblesse de l’influence du frottement, quand il s’agit de grands volumes fluides, nous conduit à rechercher s’il ne serait pas possible d’abandonner l’hypothèse d’une rotation uniforme de la nébuleuse, et à étudier les diverses hypothèses que l’on pourrait faire sur la distribution des vitesses angulaires. Cette question présente beaucoup d’analogie avec le problème suivant : Quelle sera, dans une atmosphère (par exemple l’atmosphère terrestre), la distribution stationnaire des températures ? On pourrait dire, d’une part, que si la température initiale de l’atmosphère n’est pas uniforme, elle le deviendra bientôt par suite de la conductibilité : l’état d’équilibre des températures de l’atmosphère serait donc l’état isotherme. On pourrait penser, d’autre part, supposant la conductibilité négligeable, que les mouvements internes de l’atmosphère et les brassages qui s’y produisent finiront par déterminer, pour les températures, l’état d’équilibre dit adiabatique.
L’observation montre que dans les couches les plus basses de
l’atmosphère, jusqu’à 10 kilomètres environ, on suit la loi adiabatique
parce que ces couches sont brassées constamment par les grandes
perturbations et les cyclones. Plus haut, on retrouve la loi isothermique ; plus haut encore, on ne sait rien. Quoique ni l’un ni l’autre

fig.7.
des deux états ne soit effectivement réalisé par l’atmosphère, nous
pouvons essayer d’étendre ces considérations à la distribution des rotations dans une masse fluide tournant autour d’un axe de révolution
(fig. 7). Décomposons par la pensée la masse fluide en une infinité d’anneaux très déliés, tels que AA′, tournant indépendamment
autour de Chaque anneau possédera une vitesse angulaire , et cette vitesse ω variera d’un anneau à l’autre. Si nous admettons qu’il
y ait frottement des divers anneaux les uns sur les autres, il y aura
tendance à l’uniformisation des vitesses angulaires, et deviendra
bientôt le même pour toute la masse qui, finalement, tournera d’une
seule pièce. Cet état final correspond à l’équilibre isotherme de l’atmosphère dont nous venons de parler, le frottement jouant ici le rôle que
jouait plus haut la conductibilité thermique.
Supposons au contraire que, le frottement étant négligeable, notre masse fluide soit le siège de brassages intérieurs, (ces brassages étant supposés conserver, pour simplifier, la symétrie de révolution de notre masse autour de ). Dans ce cas le moment de rotation de chaque anneau demeurera constant ; et, si on appelle la distance de chaque molécule à l’axe de rotation, l’état permanent de distribution des vitesses angulaires sera défini par l’équation
Cet état (que nous pourrons encore appeler adiabatique) est analogue à l’équilibre adiabatique des températures : chaque anneau emportant avec lui, dans son déplacement, son moment de rotation, comme tout à l’heure chaque particule de l’atmosphère conservait la même quantité de chaleur.
Remarquons que, dans cette distribution adiabatique des rotations, on aurait sur l’axe de rotation. Cet état n’est donc qu’un état limite idéal, dont on pourra s’approcher plus ou moins ; il correspond au cas d’un tourbillon rectiligne dirigé suivant l’axe.
27.Étudions les conditions d’équilibre d’une telle masse fluide tournant d’un mouvement permanent autour d’un axe de révolution (fig. 7), la vitesse angulaire n’étant plus constante, mais variant d’un anneau AA′ à l’autre. Nous reprenons les équations (3) de l’hydrodynamique dans lesquelles nous faisons , car dorénavant nous négligerons le frottement. Les trois premières équations (3) deviennent alors les équations bien connues d’Euler. Chaque molécule tournant, par hypothèse, autour de avec une vitesse angulaire , nous devons faire
et les trois premières équations (3) deviennent
| (4) |
Dans le cas d’isothermie, et sont reliés par la loi de Mariotte ; dans le cas d’adiabatie ils sont reliés par une autre formule ; mais, dans les deux cas, est fonction de et
est une différentielle exacte. Multipliant les équations (4) respectivement par et ajoutant les résultats obtenus, nous trouvons
qui s’écrit
| (5) |
en appelant
la distance d’un point à l’axe de révolution.
Le premier membre de l’équation (5) étant une différentielle exacte, il en est de même du second ; donc ne doit dépendre que de et nous pouvons poser
l’équation (5) s’écrit alors
ce qui nous donne l’intégrale
Les surfaces d’égale pression, qu’on peut encore appeler surfaces de niveau, s’obtiendront en donnant à une valeur constante ; elles auront donc pour équation
Dans l’hypothèse d’un noyau très condensé de masse nous pouvons écrire
ce qui donne pour équation des surfaces d’égale pression
Les méridiennes de ces surfaces s’obtiendront en faisant dans cette équation, ce qui donne
Telle est donc l’équation des méridiennes des surfaces de niveau lorsque la vitesse angulaire n’est plus constante, mais varie avec la distance à l’axe de révolution suivant la loi représentée par
28.La forme de ces méridiennes dépend essentiellement de la fonction . Dans le cas adopté par Laplace et par Roche, est constant ; alors
Nous retombons sur l’équation
qui a donné les courbes représentées par la figure 2 (p. 16).
Si nous supposions que la distribution des vitesses angulaires suit la loi adiabatique, nous aurions, étant une constante, les équations
et
L’équation des méridiennes serait alors
ce qui donnerait les courbes représentées par la figure 8. Les surfaces de niveau auraient donc des formes toutes différentes ne se prêtant pas à la formation d’anneaux.
Remarquons que, dans le cas de la figure 2, si l’on parcourt l’axe
depuis jusqu’à l’infini, la constante commence par décroître,
puis elle passe pur un minimum au point double A et croît ensuite

fig.8.
indéfiniment. Au contraire, dans le cas de la figure 8, la constante
part de passe par un maximum au point A, et ensuite décroît.
Donc, lorsque la quantité
| (6) |
passera par un minimum, quand varie de 0 à les méridiennes présenteront un point double et il y aura formation d’anneaux de Laplace. Lorsque cette quantité passera par un maximum, les méridiennes affecteront une forme analogue à celle de la figure 8, incompatible avec la production d’anneaux.
Dans les deux cas, qu’il y ait maximum ou minimum, la dérivée première de la quantité (6) s’annulera au point correspondant :
ce qui s’écrit
donc en ce point la force centrifuge fait équilibre à la pesanteur. Mais il n’y aura minimum, et par suite formation possible d’anneaux, que si la dérivée seconde est positive, c’est-à-dire si
ce qui s’écrit, en remplaçant par son égal ,
Cette condition exprime simplement que l’expression
croît avec Cette condition n’est pas réalisée dans la distribution dite adiabatique des vitesses, puisqu’alors on a
Nous voyons donc que, pour expliquer la formation des anneaux de Laplace, il est absolument nécessaire de supposer qu’on est très loin de l’adiabatie, et qu’on se rapproche d’une rotation uniforme de la nébuleuse.
V. — Étude de la stabilité d’un anneau. Anneaux de Saturne.
29.Quoi qu’il en soit des discussions précédentes, supposons qu’un anneau ait été formé et examinons les conditions de sa stabilité.
La question a été principalement étudiée pour la constitution et la stabilité des anneaux de Saturne. On peut faire sur la constitution de ces anneaux trois hypothèses : ils sont solides, ou fluides, ou formés d’astéroïdes indépendants très nombreux circulant autour de la planète. Nous allons voir qu’il faut rejeter les deux premières hypothèses pour des raisons mécaniques. La troisième hypothèse, proposée déjà par Cassini en 1715 mais sans preuves à l’appui, semble confirmée par l’expérience : l’anneau intérieur de Saturne est en effet transparent et la lumière le traverse sans trace de réfraction ; ce n’est donc pas un milieu continu. Les observations spectroscopiques montrent, de plus, que la vitesse d’une molécule de l’anneau n’est pas la même sur le bord interne que sur le bord externe.
30.Travaux de Laplace et de Hirn. — Laplace, supposant les anneaux de Saturne solides, a fait remarquer que, si ces anneaux étaient parfaitement réguliers, ils seraient nécessairement instables, car un anneau solide régulier, sous l’influence du plus faible déplacement provoqué par la cause la plus légère, tendrait à tomber sur la surface de la planète.
Supposons, en effet, que le centre de Saturne soit en o, le centre
de l’anneau déplacé étant en C (fig. 9). Soit ab la corde perpendiculaire en o à oC. Il est clair que l’attraction de la planète sur un
arc tel que mn, l’emporte sur son attraction sur un arc tel que m′n′.

fig.9.
Donc le segment amnb de l’anneau est plus attiré par Saturne que le
segment an′m′b. L’anneau tendra par conséquent à s’excentrer davantage et à se joindre à Saturne. Donc un anneau solide ne peut être
stable que s’il est suffisamment irrégulier.
Hirn s’est demandé, d’une part[4], dans l’hypothèse d’anneaux solides, quelle résistance on devrait attribuer à ces anneaux pour qu’ils ne soient pas brisés par l’attraction des satellites. Il est arrivé à cette conclusion : aucun corps connu, si rigide ou si tenace qu’on le suppose, ne saurait résister, sans se rompre, aux efforts qu’il aurait à supporter.
31.Calculs de Maxwell. — J. Clerk Maxwell avait aussi trouvé que les anneaux de Saturne ne pouvaient être solides, car leur stabilité exigerait alors des irrégularités si grandes qu’elles sont inadmissibles. Il examine donc l’hypothèse qui fait des anneaux de Saturne une multitude d’astéroïdes indépendants : il les assimile à des cordons de perles disposées circulairement autour de la planète et affectées de vagues régulières, soit dans le sens du rayon, soit dans le sens transversal ; chaque perle est un petit satellite. Puis il cherche les conditions pour que l’amplitude de ces vagues, nées des perturbations, ne croisse pas indéfiniment. Voici les grandes lignes de l’analyse de Maxwell[5].
32.Prenons d’abord p satellites P1, P2, … Pp, de même masse ( désignant la masse de Saturne), équidistants sur un même cercle

fig.10.
de rayon concentrique à Saturne (fig. 10). La distance de deux
satellites voisins sur ce cercle est une constante :
Un mouvement possible est celui où chaque satellite parcourrait le cercle avec une même vitesse angulaire déterminée par l’attraction de la planète à laquelle s’ajoute la force centrale due à l’attraction de tous les autres satellites. Appelons ce mouvement mouvement normal et cherchons un mouvement plan peu différent de celui-là. Désignons par
le rayon vecteur du satellite Pi et par
son angle polaire. Dans le mouvement normal non troublé, on aurait
et dans un mouvement peu différent, et seront petits ; nous négligerons leurs carrés et produits.
Écrivons, en coordonnées polaires, les équations de mouvement de l’un quelconque des satellites, par exemple du satellite P1 :
| (1) |
désigne la masse de Saturne, et
est le potentiel perturbateur dû à l’attraction de tous les autres satellites sur le satellite P1. (Nous négligeons les attractions exercées sur Saturne par les satellites, attractions qui se compensent d’ailleurs presque exactement.)
Chaque satellite donne ainsi deux équations telles que les équations (1) : il y a donc en tout 2p équations entre les et les . Ces équations devant admettre la solution
les termes indépendants des et des dans ces équations se détruiront et disparaîtront d’eux-mêmes. Si, dans ces 2p équations (1) nous ne conservons que les termes du premier ordre par rapport aux et aux , nous obtenons les équations
| (2) |
où nous avons désigné par
les parties de
qui dépendent effectivement des et des . Les seconds membres des équations (2) sont des fonctions linéaires des et des , puisque nous nous en tenons aux termes du premier ordre. Les équations (2) forment un système d’équations différentielles linéaires à coefficients constants. On pourrait, suivant la méthode classique, les intégrer par des exponentielles de la forme
| (3) |
Substituant ces valeurs dans les équations (2), on aurait un ensemble de 2p équations linéaires homogènes, entre lesquelles on éliminerait les et les On trouverait ainsi une équation de degré 4p en À chaque racine correspondrait pour les équations (2) une solution de la forme (3). Pour que le mouvement normal soit stable, il est nécessaire que et restent toujours petits. Par suite, il faudrait écrire que toutes les valeurs de ont leur partie réelle négative ou nulle. Cette méthode serait longue, aussi Maxwell procède-t-il indirectement. Il cherche pour les équations (2) une solution particulière de la forme
| (4) |
où et désignent des constantes et un entier positif. Il se trouve que, si l’on substitue à et à ces valeurs (4), les seconds membres des équations (2) prennent respectivement la forme
où sont trois constantes dépendant de l’entier . La substitution des valeurs (4) dans les équations (2) conduit donc aux deux équations
homogènes en et en et propres à déterminer et le rapport une fois choisi l’entier [6]. Par l’élimination de et de on obtient l’équation en
| (5) |
À chaque racine de cette équation du quatrième degré correspond pour les équations (2) une solution de la forme (4). Comme, dans ces formules (4), peut recevoir une série de valeurs entières[7], on conçoit la possibilité d’obtenir ainsi les intégrales générales des équations (2).
33.Remarquons que, pour une solution simple telle que la solution (4), la position et la vitesse du satellite Pi à l’époque sont les mêmes que la position et la vitesse du satellite Pi—1 à l’époque
On peut donc dire que le mouvement se communique d’un satellite à l’autre dans le temps
Chaque solution simple représente ainsi une onde ou vague élémentaire propageant le mouvement avec une vitesse angulaire égale à . Le mouvement total est la superposition des mouvements qui correspondent à plusieurs ondes élémentaires. Les ondes les plus dangereuses pour la stabilité sont les ondes courtes, c’est-à-dire celles qui correspondent aux grandes valeurs de ; pour de telles ondes, en effet, deux satellites voisins pourraient se rapprocher d’une façon sensible, et leur action mutuelle ne serait plus très petite par rapport à l’action de Saturne.
34.Pour que le mouvement normal soit stable, il faut que toutes les valeurs de soient réelles : sinon les formules (4) donneraient pour et des exponentielles en croissant indéfiniment. Montrons tout d’abord que, si le nombre des satellites est fini, on peut prendre la masse de chacun d’eux, et par suite la masse totale de l’anneau, assez petite pour assurer la réalité de toutes les valeurs de . En effet, le premier membre de l’équation (5) en est de la forme
Ce premier membre sera donc négatif si, étant très petit, on attribue à la valeur par exemple. Si donc on substitue à dans le premier membre de l’équation (5) les valeurs
on trouvera que ce premier membre prend les signes
Ces quatre changements de signe prouvent que les quatre racines de l’équation (5) sont réelles. Il y a donc stabilité si est suffisamment petit. Bien entendu, si est nul il y aura instabilité, et pourra être d’autant plus grand que le sera lui-même : la stabilité croît avec la rotation, comme il arrive pour une toupie ou un gyroscope.
Si désigne le rapport de la masse de tous les satellites à la masse de Saturne. Maxwell a montré ainsi, qu’il faut, pour qu’il y ait stabilité, que
On voit que si le nombre des satellites augmente indéfiniment, leur masse totale (c’est-à-dire la masse de l’anneau) doit tendre vers zéro ; c’est là un inconvénient de la théorie de Maxwell ; mais c’est un inconvénient artificiel, car l’hypothèse d’un grand nombre de petits satellites répartis sur une seule circonférence est trop simple. Il faudrait supposer une distribution des satellites occupant un certain volume de l’espace ; alors la difficulté signalée disparaîtrait.
35.Limite supérieure de la densité d’un anneau fluide. — Maxwell étend son analyse au cas d’un anneau supposé fluide. Malheureusement, dans cette partie de son Mémoire, les raisonnements manquent parfois de rigueur et même de clarté, aussi faut-il les considérer seulement comme un aperçu, dont la conclusion semble néanmoins, devoir être acceptée.
Décomposons l’anneau supposé fluide en un grand nombre de tranches MNM′N′ par des plans méridiens (fig. 11) et assimilons chaque

fig.11.
tranche à un des satellites précédents Pi. Il s’agit de calculer les
seconds membres des équations (2), c’est-à-dire (en effaçant l’indice i)
On peut concevoir que la quantité
puisse être faite égale à zéro, car elle représente (à un facteur près) le travail élémentaire dû, dans un déplacement radial de la tranche, aux inégalités de l’anneau ; or, ce travail est très petit.
Calculons à présent la quantité
qui représente (à un facteur près) le travail élémentaire dû aux inégalités de l’anneau, dans un déplacement tangentiel de la tranche.
Appelons la densité du fluide dans le mouvement normal et sa densité dans le mouvement troublé. Le théorème de Poisson donne
c’est-à-dire
| (5′) |
puisque dans le mouvement normal on a
Si nous adoptons, pour un instant, un axe des tangent à la circonférence moyenne de l’anneau, nous reconnaissons que la dérivée
est bien plus grande que les deux autres, car c’est dans le sens des que l’onde de condensation se propage, et nous choisissons les ondes les plus défavorables à la stabilité, c’est-à-dire les plus courtes ; l’onde étant très courte les variations dans le sens de la propagation, c’est-à-dire dans le sens de l’axe des sont très rapides ; nous pouvons donc écrire, au lieu de l’équation (5′),
| (6) |
La contraction a eu pour effet de multiplier la densité de la tranche par
elle a multiplié son épaisseur par
comme sa masse totale n’a pas changé, on doit avoir
c’est-à-dire
Alors l’équation (6) donne la suivante :
d’où l’on tire, en intégrant,
Le second membre de la seconde équation (2) est donc
nous avons vu d’ailleurs que le second membre de la première équation (2) peut être pris égal à zéro.
Si maintenant dans les équations (2) nous substituons les valeurs (4) de et de , nous obtenons
et l’élimination de et de entre ces équations conduit à l’équation en
ou
Cette équation bicarrée en doit, s’il y a stabilité, avoir ses racines réelles, ce qui exige que
cette inégalité peut s’écrire ainsi :
Nous savons déjà que la masse de l’anneau et, par suite, sa densité doivent être petites pour qu’il y ait stabilité. Négligeant donc , nous obtenons la condition
d’où nous tirons l’inégalité
| (7) |
qui fixe une limite supérieure à la densité de l’anneau. Maxwell conclut que si l’anneau était liquide sa densité ne pourrait pas surpasser 1300 de celle de la planète. Ce résultat est vrai pour un anneau de poussières cosmiques comme pour un anneau liquide : la stabilité ne peut exister que si la densité est suffisamment petite.
36.Limite inférieure de la densité d’un anneau fluide. — Un calcul que nous avons déjà fait à la fin de la Section II (p. 23), donne une limite inférieure pour la densité d’un anneau fluide homogène supposé tourner d’une seule pièce avec la vitesse angulaire l’anneau n’est stable que si sa densité satisfait à l’inégalité
| (8) |
Le même raisonnement nous permet même de dire que, pour une masse fluide homogène tournant autour d’un axe avec une vitesse angulaire constante et soumise à l’attraction mutuelle de ses molécules, aucune figure n’est stable si l‘inégalité (8) n’est pas satisfaite[8]. Si, dans cette inégalité, nous prenons pour la vitesse angulaire d’un satellite dont l’orbite coïnciderait avec l’anneau de Saturne, nous trouvons que la densité de l’anneau doit être supérieure à 116 de celle de la planète. Cette condition est incompatible avec celle de Maxwell et elle nous force à rejeter l’hypothèse de la fluidité des anneaux de Saturne. Comme ces anneaux ne sont pas non plus solides, d’après Maxwell et d’après Hirn, nous sommes amené à les regarder comme formés d’un grand nombre de corpuscules indépendants : le calcul de Maxwell nous a appris qu’une telle constitution peut être stable si la masse totale de l’anneau est assez petite.
37.La limite inférieure de la densité, donnée par l’inégalité (8), a été trouvée en supposant que la vitesse angulaire est la même pour tout le fluide. Affranchissons-nous de cette hypothèse et considérons, comme dans la Section IV, une masse fluide tournant d’un mouvement permanent autour d’un axe de révolution (fig. 7, p. 30), la vitesse angulaire variant d’un anneau élémentaire AA′ à l’autre. Conservant les notations de la section IV, nous avons (p. 32) la relation
Or, la pression est nulle à la surface et positive à l’intérieur du fluide ; donc
présente un maximum à l’intérieur ; par conséquent il en est de même de l’expression
Il y a donc certainement, à l’intérieur de la masse fluide, un point (ou plusieurs) où l’on a
| (9) |
Or, rappelons-nous que ne dépend que de la distance
à l’axe de rotation ; on a
et comme on a (p. 32)
il vient
d’ailleurs, le théorème de Poisson donne
L’inégalité (9) montre donc qu’il existe à l’intérieur de la masse fluide des points satisfaisant à la condition
| (10) |
Si nous supposions que ne varie pas avec nous retrouverions la limite inférieure de la densité donnée par l’inégalité (8).
38.Nous pouvons même serrer davantage l’inégalité (10). Considérons un anneau fluide dont la méridienne est QQ’ et qui tourne

fig.12.
autour de son axe (fig. 12). Nous venons de dire qu’il existe à
l’intérieur du fluide des points A où est maximum ; le lieu de ces points est ici un cercle d’axe et du rayon oA. Or, en un point
où est maximum, on a, non seulement
mais encore
| (11) |
Pour l’anneau de Saturne nous pouvons poser
étant le potentiel dû à l’attraction de Saturne et étant le potentiel dû à l’attraction de l’anneau sur lui-même. Calculons séparément les trois dérivées secondes en de
au point A de l’axe des (fig. 12) où passe par un maximum. Nous trouvons qu’on a, en ce point A,
et sont de petites quantités positives ; d’ailleurs, au point A considéré, diffère peu de (troisième loi de Képler), et l’on peut écrire approximativement
Il est aisé de se rendre compte de l’erreur commise en écrivant ces équations ; on a remplacé par ; l’équation exacte s’obtient en écrivant
L’erreur commise est donc de l’ordre de ; si les dimensions de la section méridienne de l’anneau sont très petites par rapport au rayon de l’anneau (c’est-à-dire par rapport à ou à ) sera de l’ordre de ; étant l’une des dimensions de la section méridienne, il sera donc négligeable non seulement d’une manière absolue, mais devant , c’est-à-dire devant et qui sont du même ordre que .
Alors les trois inégalités (11) donnent les trois suivantes
La première et la troisième sont satisfaites d’elles-mêmes. De la seconde on tire, en remplaçant par , et se rappelant que et sont positifs, l’inégalité
| (12) |
donnant pour la densité une limite inférieure plus précise que la limite donnée par l’inégalité (10).
Si donc la distribution des vitesses angulaires dans l’anneau est telle que le premier membre de l’inégalité (12) soit positif, il existera une limite inférieure de la densité ; si, au contraire, ce premier membre est négatif il n’en existera pas : or, ce premier membre est positif ou négatif suivant que croît ou décroît quand augmente.
VI. — Rupture des anneaux de Laplace. Formation des planètes.
39.Revenons maintenant aux anneaux abandonnés par la nébuleuse de Laplace dans le plan de son équateur, et montrons qu’il arrivera un moment où ils seront nécessairement instables. Nous venons de trouver, dans la Section précédente, une limite supérieure et une limite inférieure pour la densité d’un anneau fluide. Pour qu’il y ait stabilité on doit avoir à la fois, d’après les inégalités (7) et (12),
| (13) |
À l’instant où l’anneau est abandonné, sa densité est très petite, donc la première inégalité est vérifiée. De plus, les particules de l’anneau se mouvant selon la troisième loi de Képler, on a
et par suite, en différentiant et en divisant par
la seconde inégalité est donc vérifiée aussi.
Donc l’anneau est stable au début. Mais cet état de choses ne peut pas durer. D’abord, par suite du refroidissement, la densité augmentera et la première inégalité pourra cesser d’être satisfaite. Ensuite, le frottement des couches les unes sur les autres tendra, d’après Laplace, à uniformiser la vitesse angulaire qui deviendra constante : la dérivée devenant nulle, les deux inégalités (13) deviennent incompatibles, et l’anneau ne peut pas subsister.
40.D’ailleurs, une cause autre que le frottement agit pour rendre uniforme et nul. Cette cause est celle qu’indique Laplace et que nous avons déjà signalée (Chap. I, p. 10, fig. 1). À l’instant où l’anneau est abandonné, la troisième loi de Képler donne, entre la vitesse angulaire d’une particule et sa distance au centre, la relation
| (14) |
À une époque ultérieure , l’anneau s’est rétréci et a diminué d’épaisseur par suite du refroidissement ; le moment de rotation de chaque particule étant demeuré constant, la nouvelle vitesse angulaire et la nouvelle distance au centre vérifient l’équation
| (15) |
Comparant l’équation (14) à l’équation (15) il vient
| (16) |
L’anneau étant très mince, nous prenons pour unité son rayon moyen et nous posons
et étant de petites quantités. La contraction étant mesurée par le rapport on a
la vitesse angulaire à l’époque est donnée par l’égalité (16) qui s’écrit
Quand la contraction aura atteint la valeur aura atteint, on le voit, une valeur constante
Ce mécanisme concourt donc avec le frottement à uniformiser la vitesse de rotation de l’anneau et à la rendre constante, les particules les plus externes acquérant ainsi une vitesse linéaire plus grande que les plus internes, comme le voulait Laplace pour expliquer la rotation directe des planètes. Malheureusement l’anneau deviendra instable avant que cet état de rotation uniforme ne soit atteint, puisque les deux inégalités (13) seront devenues incompatibles.
41.L’anneau, n’étant plus stable, se rompra en plusieurs parties, qui ne seront encore que des masses gazeuses plus ou moins diffuses, décrivant chacune un cercle autour du Soleil, à la façon d’un satellite. Si toutes ces masses gazeuses étaient juste à la même distance du Soleil elles n’arriveraient pas à se rencontrer. Mais, si leurs distances au Soleil sont un peu différentes, leurs vitesses angulaires le seront aussi, et par suite l’une des masses rejoindra l’autre : si la différence de leurs distances au Soleil est plus petite que la somme des rayons des deux masses, celles-ci se choqueront et se réuniront en une seule. Nous comprenons ainsi comment les diverses masses en lesquelles s’est brisé l’anneau peuvent arriver à se réunir en une seule et à donner une planète unique.
42.Cause de la rotation directe. — Il s’agit maintenant d’expliquer
pourquoi cette planète aura en général un mouvement de rotation
direct, puisque l’explication de Laplace est insuffisante. Considérons
deux masses gazeuses M et M′ provenant de la rupture de l’anneau
et dont les distances au Soleil sont un peu différentes (fig. 13).

fig.13.
D’après la troisième loi de Képler la masse la plus éloignée M′ a
une vitesse moindre que la plus rapprochée M : c’est donc M qui
rejoindra M′, viendra la choquer et se coller à elle. Il semble, à première vue, que la planète résultant de ce choc aura un mouvement de
rotation rétrograde, puisque ses parties internes auront des vitesses
plus grandes que ses parties externes. Mais la masse gazeuse globuleuse, grossièrement ronde, résultant de la réunion de M et de M′,
n’est pas soustraite à toute action extérieure. Elle subit l’attraction
du Soleil ; cette attraction lui fera prendre une forme allongée vers
cet astre, l’attraction solaire tendant toujours à ramener son grand
axe dans cette direction. Il se produira donc dans la masse des
marées internes considérables accompagnées de frottements, qui
tendront à rendre égales la durée de rotation et la durée de révolution. Ce mécanisme ne diffère pas de celui qu’invoquait Laplace pour
expliquer le fait que la Lune présente toujours à la Terre le même
hémisphère (Chap. II, p. 13.)
La masse planétaire arrivera donc à présenter une durée de rotation égale à sa durée de révolution, et à ce moment sa rotation sera devenue directe. La condensation augmentant par suite du refroidissement, cette vitesse de rotation directe tend à augmenter ; mais les marées tendent à la maintenir égale à celle de révolution. Au début, l’influence des marées l’emportera et les deux vitesses seront égales ; puis, l’influence des marées diminuant, la masse planétaire commencera à présenter une libration ; enfin, la condensation se poursuivant, l’influence des marées cessera d’être prépondérante et il y aura une rotation directe plus rapide que la révolution (voir au Chap. VII ce que nous disons à propos de la théorie de Darwin). L’action des marées diminue, en effet, à mesure que la contraction se poursuit, car la marée sur un astre dépend de la différence entre l’attraction solaire à la surface de cet astre et l’attraction solaire en son centre ; cette différence est évidemment plus faible pour un petit astre que pour un gros.
Cette explication de la rotation directe de la plupart des planètes, fondée sur l’action des marées est, semble-t-il, la meilleure. Si les planètes les plus extérieures (Uranus et Neptune) ont une rotation rétrograde, c’est, sans doute, que leur très grand éloignement a rendu la marée solaire très faible et insuffisante à produire la rotation directe.
VII. — Formation des satellites.
43.Nous venons de nous rendre compte comment un anneau de Laplace, en se rompant, a pu se transformer en une masse sphéroïdale généralement animée d’un mouvement de rotation direct. Cette masse sphéroïdale, que nous appellerons nébuleuse planétaire, pourra à son tour engendrer une planète accompagnée de satellites. Cette nébuleuse planétaire, en effet, est comparable à la nébuleuse solaire, mais sous de moindres proportionne Elle pourra, par l’effet de la condensation, abandonner le long de son équateur des anneaux nébuleux qui finiront par engendrer des satellites.
Toutefois, tandis que la nébuleuse solaire, libre de toute action extérieure, présentait une figure de révolution autour de son axe de rotation, la nébuleuse planétaire est soumise à l’influence de l’attraction solaire qui y produit des marées ; sous cette influence la nébuleuse planétaire s’allonge dans le sens du Soleil et tend à tourner constamment vers cet astre les mêmes points de sa surface. Ainsi s’établit, comme nous l’avons dit, l’égalité entre les durées de rotation et de révolution de la nébuleuse planétaire. Cette égalité qui, pour une raison analogue, a lieu encore aujourd’hui pour la Lune et probablement pour plusieurs satellites, ainsi peut-être que pour les planètes Mercure et Vénus, a dû se rencontrer chez toutes les planètes dans la première phase de leur existence.
Tant que s’est maintenue cette égalité, la nébuleuse planétaire a dû rester dans des conditions impropres à la formation de satellites. En effet, son volume diminuait par suite de la contraction, mais la vitesse restait la même ; donc diminuait, condition incompatible avec la production d’anneaux, ainsi que nous l’avons vu dans la Section III. Si l’égalité entre les durées de rotation et de révolution a lieu encore actuellement pour tous les satellites, nous nous expliquons pourquoi il n’y a pas de satellites du second ordre.
44.Étudions de plus près et analytiquement les conditions où s’est trouvée la nébuleuse planétaire dans cette première phase où elle tournait sur elle-même dans un temps égal à celui de sa révolution. D’abord, on peut faire au sujet de sa constitution deux hypothèses très différentes : on peut la supposer à peu près homogène, ou bien avec une très forte condensation centrale. Pour la nébuleuse solaire, la seconde hypothèse s’imposait à l’exclusion de la première (Section II). Mais pour une nébuleuse planétaire elle ne s’impose pas autant, et il y a lieu d’examiner successivement les deux hypothèses.
45.Cas d’une masse homogène. — Étudions donc en premier lieu les conditions d’équilibre d’une masse fluide homogène animée d’un mouvement de rotation uniforme autour d’un axe de direction fixe passant par son centre de gravité o ; cette masse est soumise à l’attraction mutuelle de ses parties, et aussi à l’attraction d’un astre éloigné C (Soleil) situé dans le plan de l’équateur. Nous supposerons que, en vertu de cette dernière force, le point o décrit un cercle ayant son centre en C, et que la durée de révolution est égale à la durée de la rotation de la masse fluide autour de [9]. Ce sont bien là des conditions analogues à celles où se trouvait la nébuleuse planétaire que nous étudions.
Prenons pour axes rectangulaires mobiles (fig. 14) l’axe de rotation
, l’axe dirigé vers le Soleil C et l’axe perpendiculaire aux

fig.14.
deux précédents. Dans ces conditions, la théorie élémentaire des
marées nous apprend que le potentiel perturbateur dû à l’attraction
solaire est
désignant la masse du Soleil et sa distance au point o. Si est la masse du fluide en mouvement, la troisième loi de Képler donne l’équation
d’où nous tirons, en appelant
le rapport de la masse fluide à la masse solaire,
par suite nous pouvons écrire
Le potentiel dû à la force centrifuge est
Nous voulons prouver que la masse fluide homogène peut prendre, dans l’équilibre, la figure d’un ellipsoïde
| (17) |
dont les axes sont dirigés suivant On sait que Ie potentiel d’attraction à l’intérieur d’un tel ellipsoïde homogène peut s’écrire
étant trois constantes. Si l’on désigne par
| (18) |
les carrés des rapports d’un des axes de l’ellipsoïde aux deux autres, ces trois constantes ont pour valeurs
| (19) |
où l’on a posé
Donc, lorsque la masse homogène affecte la forme de l’ellipsoïde (17), le potentiel total a pour valeur
Pour montrer que l’ellipsoïde (17) est une figure d’équilibre, il suffit de faire voir qu’un peut l’identifier avec une surface équipotentielle
cette dernière équation s’écrit
et l’identification avec l’équation (17) donne
Avec la notation (18), ces deux dernières équations s’écrivent, on le voit de suite,
Ce sont deux équations aux deux inconnues et : elles détermineront les rapports des axes de l’ellipsoïde qui est une figure d’équilibre. Si nous posons
ces deux équations s’écrivent, en remplaçant par leurs valeurs (19),
| (20) |
Puisque est essentiellement positif, et seront toujours plus petits que 1, c’est-à-dire que l’axe de rotation sera toujours le petit axe de l’ellipsoïde.
46.La seconde des équations (20) peut être considérée comme représentant une courbe dans le plan des . Si nous construisons la portion de cette courbe intérieure au carré
nous trouvons qu’elle a la forme représentée sur la figure (15) : elle se
compose de deux branches AB et OD. Pour la branche AB, nous
avons : l’ellipsoïde a son grand axe dirigé vers le Soleil, ce qui
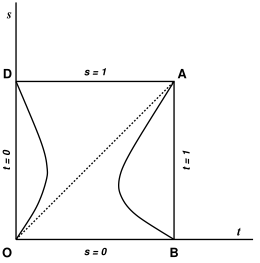
fig.15.
correspond à des formes stables. Au point A l’ellipsoïde se confond
avec une sphère, au point B c’est une aiguille infiniment allongée, à
section circulaire. La branche OD pour laquelle correspond
à des ellipsoïdes allongés dans une direction perpendiculaire à celle
du Soleil ; ces ellipsoïdes sont des figures toutes instables. Au point D
l’ellipsoïde est une aiguille très allongée à section circulaire, au
point O c’est une aiguille très allongée et à section aplatie.
Si l’on examine comment varie
lorsqu’on chemine sur ces deux branches de courbe, on reconnaît que partant de 0 au point A, commence à croître, passe par un maximum, puis reprend en B la valeur 0. De même part de 0 au point D, passe par un maximum et s’annule de nouveau au point O.
Si l’on considère le moment de rotation, on constate que, nul en A, il ne cesse de croître le long de la branche AB et devient infini en B (en ce point B, le moment de rotation est infini, bien que la vitesse angulaire soit nulle, car le moment d’inertie de l’aiguille infiniment allongée est infini).
47.Étudions spécialement deux cas particuliers. Soit d’abord
, c’est-à-dire que la masse de l’astre perturbateur C est supposée négligeable par rapport à la masse liquide en rotation. La
question revient alors à chercher les formes d’équilibre d’une masse
fluide homogène animée d’une rotation uniforme et soustraite à toute
action extérieure, problème connu : les deux branches de courbe AB
et OD de notre représentation graphique se rejoignent alors en un
point H, et la figure 15 se transforme en la figure 16 ; la ligne OA
bissectrice des axes de coordonnées correspond à des ellipsoïdes de
révolution (ellipsoïdes de Mac-Laurin) ; la ligne DB correspond à des
ellipsoïdes à trois axes inégaux (ellipsoïdes de Jacobi).
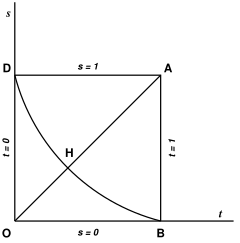
fig.16.
48.Le second cas particulier que nous envisagerons est celui de La masse fluide en rotation est alors très petite par rapport à la masse de l’astre troublant C (c’est le cas d’une nébuleuse planétaire dont la masse est très petite par rapport à celle du Soleil). Dans ce cas, la branche OD de la figure 15 vient s’aplatir contre l’axe des tandis que la branche AB subsiste. Quand on parcourt cette branche AB, la quantité part de 0, passe par un maximum égal à 0,046, puis décroît jusqu’à 0. Pour qu’une forme ellipsoïdale d’équilibre soit possible, il est donc nécessaire que l’on ait
Cette inégalité va fournir une limite supérieure que n’a pas pu dépasser le diamètre d’une nébuleuse planétaire (supposée ellipsoïdale et homogène). Prenons, par exemple, la nébuleuse planétaire qui a engendré Jupiter. Si désigne un rayon moyen de l’ellipsoïde qu’était initialement cette nébuleuse, la masse de celle-ci ( est approximativement la masse de Jupiter) est égale à
| (21) |
d’ailleurs, désignant la distance de Jupiter au Soleil dont la masse est on a
| (22) |
La comparaison de l’égalité (21) et de l’égalité (22) donne
Puisqu’il faut que
et que
environ, on voit que le rayon moyen de la nébuleuse de Jupiter devait satisfaire à l’inégalité
d’où l’on tire
Or (le rayon de l’orbite terrestre étant pris pour unité) ; donc
Prenant pour unité le rayon de Jupiter, cette inégalité signifie que doit être inférieur à 440 rayons de Jupiter.
Ainsi la nébuleuse planétaire qui a engendré Jupiter et son cortège de satellites n’a pas dû avoir initialement un rayon moyen supérieur à 440 rayons actuels de Jupiter. Les satellites n’ont donc pas dû se former à une distance plus grande. En effet, le plus éloigné des satellites actuellement connus est à une distance de la planète égale à 357 rayons. Mais, si l’on venait à découvrir un satellite à une distance notablement[10] supérieure à 440 rayons, il y aurait là un sérieux argument contre la théorie.
49.Cas d’une masse à forte condensation. — Envisageons à présent l’hypothèse où la nébuleuse planétaire, qui tourne autour du Soleil en un temps égal à celui de sa rotation, présenterait une très forte condensation centrale de masse et cherchons la figure d’équilibre relative de son atmosphère.
Adoptons les mêmes axes de coordonnées que précédemment (fig. 14). Le potentiel d’attraction dû à la condensation est (nous négligeons l’attraction mutuelle des molécules de l’atmosphère) ; le potentiel dû à la force centrifuge est
le potentiel total est
représentant le potentiel dû à l’action perturbatrice du Soleil, situé en C sur l’axe des (potentiel que nous avons appelé plus haut ).
Les surfaces de niveau ont pour équation
Lorsque est nul, nous retrouvons l’équation déjà discutée (Section I), et les surfaces sont de révolution : l’une d’elles présente un cercle double équatorial formant arête saillante. Mais il n’en est plus de même lorsque n’est pas nul. Dans ce cas, l’une des surfaces acquerra un point double si l’on a à la fois
La première de ces équations est vérifiée dans le plan , par raison de symétrie ; les deux autres, en prenant des coordonnées polaires, c’est-à-dire en posant
sont équivalentes à
Ces deux dernières nous donneront les coordonnées polaires du point double ; on aura
étant très petit, cette équation donne approximativement
Ayant ainsi la distance , nous la portons dans l’équation
qui donnera l’azimut du point double. Comme
nous voyons qu’en ce point double la fonction passera (en tant que fonction de ), par un maximum ou par un minimum : on reconnaît aisément qu’elle passera par un maximum.
Dans le cas actuel, la fonction perturbatrice due à l’action solaire a pour expression
désignant comme plus haut la masse du Soleil et sa distance au centre. Elle présente, pour une valeur donnée de , deux maxima égaux, en deux points de l’axe des
Donc l’une de nos surfaces de niveau présente deux points doubles ou points coniques ; les surfaces de niveau extérieures à celle-là ne sont plus fermées.
50.Jusqu’ici la durée de rotation de la nébuleuse planétaire a été supposée égale à sa durée de révolution, et nous avons dit (no 43) que, pendant toute la période où s’est maintenue cette égalité, la nébuleuse n’a pas dû former de satellites. Lorsque, par suite de la condensation, la marée solaire est devenue plus faible, la rotation s’est accélérée, et la nébuleuse planétaire a cessé de présenter constamment au Soleil les mêmes points de sa surface. Roche admet que, dans cette seconde période, l’atmosphère planétaire prend à chaque instant la figure avec laquelle elle pourrait être en équilibre sous l’action du Soleil : sa surface libre est allongée vers le Soleil, et peut acquérir, aux sommets du grand axe, deux points coniques comme ceux dont nous parlions plus haut. C’est par ces deux pointes opposées que la contraction laissera s’échapper l’excès de fluide atmosphérique, et non plus par toute une arête saillante équatoriale, comme il arrivait pour la nébuleuse solaire de révolution. Donc, au lieu d’un anneau régulièrement disposé autour de la planète, nous aurions une émission de matière s’effectuant par deux points opposés. Roche pense que les diverses masses ainsi délaissées ne présenteraient aucune condition de stabilité ni de durée, et qu’en réalité les satellites ne se sont pas formés dans cette seconde période : ils appartiendraient à une phase bien postérieure ou la durée de la rotation se trouvait déjà tellement réduite que l’allongement de la nébuleuse planétaire vers le Soleil était presque négligeable. La nébuleuse planétaire, devenue alors tout à fait comparable à la nébuleuse solaire, aurait abandonné des anneaux ordinaires de Laplace qui auraient engendré les satellites.
Dans ce cas, aucun satellite ne se serait formé avant que la nébuleuse planétaire ne soit assez contractée pour que la différence entre son plus grand et son plus petit rayon équatorial, soit descendue au dessous d’une certaine limite . Estimant assez arbitrairement cette limite à 4,5 rayons terrestres, Roche en conclut, pour le rayon des différentes nébuleuses planétaires, au moment où elles ont pu commencer à abandonner des anneaux équatoriaux, les valeurs suivantes (exprimées en rayons de la planète correspondante) :
| Jupiter | | Saturne | | Uranus | | Neptune |
| 48,6 | 64,4 | 155 | 200 |
C’est seulement en deçà de ces distances qu’on doit s’attendre à trouver des satellites. Les satellites anciennement connus satisfont bien à cette condition. Mais il n’en est plus de même pour certains satellites récemment découverts : pour Jupiter, par exemple, on connaît un satellite à une distance de la planète égale à 357 rayons. Il y a donc lieu de penser que, contrairement à l’opinion de Roche, les masses gazeuses abandonnées par les deux points coniques de la nébuleuse dans la seconde phase de son existence ont pu concourir à la formation de satellites. Cela, en effet, ne paraît pas impossible à imaginer : les masses successivement abandonnées auraient pu se répartir sur un anneau ; mais si, ce qui est le plus probable, aucun anneau n’avait pu se former, on se serait précisément trouvé dans les mêmes conditions qu’après la rupture de l’anneau devenu instable. Que cet état ait été atteint en passant par une phase d’anneau stable, ou sans passer par cette phase, la formation d’un satellite aurait toujours pu en résulter par un mécanisme identique.
51.Cas de la Lune. — Roche estime que la Lune se présente, à divers points de vue, comme un satellite exceptionnel.
« Elle se distingue, dit-il, par la grandeur de ses dimensions et de sa masse comparées à celles de la Terre, par l’excentricité de son orbite, surtout par sa distance à la Terre. Saturne et peut-être Uranus en ont un aussi éloigné comparativement au rayon de la planète, mais c’est alors le dernier d’une série de satellites. Ici le satellite est unique. » (Essai sur la constitution et l’origine du système solaire, n° 52.)
Ces raisons lui font attribuer à la Lune une origine spéciale :
« Il a pu arriver aussi exceptionnellement, et telle est l’origine probable de la Lune, qu’un amas de vapeurs déjà refroidies s’étant formé au dedans de la nébuleuse terrestre, dans la région équatoriale et à une certaine profondeur, cet amas soit devenu un centre de condensation autour duquel se sont groupés d’autres amas semblables. De cette agglomération est résultée, dans l’atmosphère même de la Terre, une nouvelle nébuleuse, origine de la Lune. » (loc. cit., n° 58.)
Le système Terre-Lune serait donc, comparable, dans cette manière de voir, à une sorte de planète double. Nous sommes donc très loin des idées de Laplace.
52.Anneau de Saturne. — Pourquoi le dernier anneau équatorial abandonné par la nébuleuse de Saturne est-il resté sous forme d’anneau et n’a-t-il pas donné un satellite ? C’est, d’après Roche, parce qu’à une aussi faible distance de la planète, une masse fluide ellipsoïdale n’aurait pas pu être en équilibre. Rappelons-nous en effet ce que nous avons dit relativement à une masse fluide homogène, soumise à l’attraction d’un astre central éloigné (ici Saturne) et animée d’une rotation uniforme d’une durée égale à celle de sa révolution. Lorsque la masse fluide est très petite par rapport à celle de l’astre central (cas de ), nous avons vu (n° 48) qu’il faut avoir
pour qu’une forme ellipsoïdale d’équilibre soit possible. Mais la troisième loi de Képler donne
désignant ici la masse de Saturne et sa distance à la masse fluide ; il faut donc que
Remplaçons par et étant le rayon et la densité de Saturne, l’inégalité précédente devient
Si, pour fixer les idées, on suppose les deux densités égales, la condition d’existence du satellite fluide est simplement
D’où cette conclusion : à une distance de la planète inférieure à deux fois et demie son rayon, un satellite de même densité à l’état fluide ne saurait se maintenir sous forme ellipsoïdale. Comme le rayon moyen de l’anneau de Saturne est inférieur à cette distance, sa matière n’a donc pas pu s’agglomérer en un corps unique. Cela appelle les observations suivantes : à cette distance une forme annulaire fluide ou solide est instable ; nous l’avons vu et nous en avons conclu que l’anneau se composait de satellites très petits et ellipsoïdaux. Mais d’après Roche, une figure ellipsoïdale (en supposant l’égalité des vitesses de révolution et de rotation) est également instable. Nous devons donc conclure que les petits satellites dont est composé l’anneau ne présentent pas toujours la même face à Saturne.
VIII. — Objections à la Théorie de Laplace.
53.Nous avons exposé en détail les développements théoriques auxquels ont donné lieu les idées de Laplace. Voyons maintenant les quelques objections que l’on peut faire et que l’on a faites en effet à cette théorie.
Le but de Laplace était de rendre compte de la faiblesse des excentricités et des inclinaisons, et du sens direct de tous les mouvements connus de son temps. Son hypothèse explique fort bien les deux premiers de ces phénomènes ainsi que le sens direct de toutes les révolutions des planètes. Quant aux rotations directes, elles sont, avons-nous dit, insuffisamment expliquées par Laplace ; mais nous avons pu en rendre compte d’une façon satisfaisante au moyen de l’effet produit par les marées solaires sur les nébuleuses planétaires (mécanisme qui n’avait pas échappé à Laplace en ce qui concerne la Lune). La marée solaire étant très faible pour les planètes les plus extérieures, nous répondons du même coup à l’objection qu’on pourrait tirer des mouvements rétrogrades des systèmes d’Uranus et de Neptune.
54.On a aussi objecté à la théorie de Laplace l’énormité du temps nécessaire à la transformation d’un anneau en une masse planétaire unique. Un anneau devenu instable s’est rompu en plusieurs masses sphéroïdiques qui, d’après Laplace, ont dû se réunir en une seule. Or, M. Kirkwood a fait remarquer que cette réunion exigerait un temps considérable. Si les fragments de l’anneau étaient distribués à peu près régulièrement le long de l’orbite, leurs actions perturbatrices se détruiraient à très peu de chose près, et on ne pourrait invoquer en faveur de la réunion des morceaux un peu éloignés que la différence de leurs vitesses de révolution. Or, considérant deux fragments de l’anneau de Neptune distants de 180° en longitude, et dont les distances au Soleil différeraient de 1 000 milles, M. Kirkwood calcule que leur jonction ne se ferait qu’au bout de 150 millions d’années. Pendant ce temps les masses se seraient refroidies et encroûtées, et cette durée semble beaucoup trop considérable, étant donné l’âge que la Thermodynamique permet d’assigner au système planétaire. Pour échapper à cette grave difficulté, M. Kirkwood propose d’admettre que les planètes ont été projetées par des espèces d’éruptions solaires : elles seraient en quelque sorte assimilables à d’anciennes protubérances que le Soleil aurait comme oubliées en se contractant. Mais dans cette supposition, on ne trouve aucune raison pour expliquer la faible excentricité des orbites. D’ailleurs nous n’avons aucune espèce d’idée du temps qui a pu être nécessaire pour la formation du système solaire. Il est possible, il est probable même que 150 millions d’années ne représentent qu’une fraction très faible de ce temps. Il n’y a donc rien à retenir de l’objection de M. Kirkwood.
55.Une autre difficulté de l’hypothèse de Laplace provient de ce que plusieurs satellites sont à des distances de leur planète incompatibles avec cette hypothèse. On a dit, par exemple, que la distance de la Lune à la Terre est plus grande que n’a pu être le rayon de l’atmosphère terrestre à l’époque de la formation de la Lune, c’est-à-dire lorsque la nébuleuse terrestre tournait sur elle-même en 27jours,3, durée de la révolution de la Lune. La limite de l’atmosphère de cette nébuleuse était en effet le point où la force centrifuge jointe à l’attraction solaire contrebalançait l’attraction terrestre, et l’on a cru pouvoir en déduire que l’atmosphère terrestre ne s’étendait qu’aux trois quarts de la distance de la Lune à la Terre. Mais Roche a montré que cette affirmation est inexacte. Dans le calcul de cette limite de l’atmosphère, ce qui intervient, ce n’est pas l’attraction absolue du Soleil, mais, comme dans le calcul des marées, son attraction relative, c’est-à-dire la différence entre l’attraction exercée sur une molécule de l’atmosphère et l’attraction exercée sur le centre de la Terre. On trouve, avec cette rectification, qu’à l’époque indiquée l’atmosphère terrestre atteignait la distance de la Lune. La grande distance de la Lune n’est donc pas une objection à la théorie de Laplace.
Il n’en est pas de même pour les petites distances auxquelles se trouvent le premier satellite de Mars et l’anneau intérieur de Saturne. D’après l’hypothèse de Laplace, « tous les corps qui circulent autour d’une planète ayant été formés par les zones que son atmosphère a successivement abandonnées, et son mouvement de rotation étant devenu de plus en plus rapide, la durée de ce mouvement doit être moindre que celles de la révolution de ces différents corps. » (Exposition du Système du Monde, p. 503). Or, on sait que le satellite le plus voisin de Mars (Phobos) et l’anneau intérieur de Saturne ont une durée de révolution moindre que la durée actuelle de rotation de la planète. On peut, pour expliquer cette anomalie, avoir recours à la formation d’anneaux intérieurs par la rencontre de traînées elliptiques, telle qu’elle a été indiquée par Roche (n° 24). Le satellite de Mars se serait ainsi formé à l’intérieur même de l’atmosphère primitive de la planète, c’est-à-dire à une distance inférieure à celle que lui avait assignée Laplace. Ce satellite aurait ensuite subi la résistance de milieu de cette atmosphère, ce qui aurait pu contribuer à rétrécir son orbite et, par conséquent, à augmenter sa vitesse de révolution. L’hypothèse de Laplace est ainsi sauvée, mais au prix d’une modification profonde.
56.Enfin la découverte récente, autour de Jupiter et de Saturne, de satellites à révolution rétrograde, crée une nouvelle difficulté. On pourrait essayer de la lever en considérant, comme au n° 42 (p. 51), deux masses et provenant de la rupture de l’anneau (fig. 13) ; la masse sera supposée très petite, la masse , provenant de la réunion antérieure de plusieurs noyaux, sera supposée très grande. Lorsque la masse rejoindra et dépassera la masse , elle pourra ne pas la choquer, mais elle pourra la capter (si cette masse secondaire pénètre dans l’atmosphère de la masse principale, et si la résistance de cette atmosphère réduit la vitesse relative des deux masses) et s’en faire un satellite à révolution rétrograde. On pourrait supposer également que le satellite s’est formé par le mécanisme ordinaire à l’époque où la rotation de la nébuleuse planétaire était encore rétrograde. Le mécanisme de la marée solaire continuant à agir sur la masse planétaire, celle-ci prendra un mouvement de rotation direct, et les satellites ultérieurement formés seront à révolution directe.
- ↑ Les travaux de E. Roche sur ce sujet se trouvent résumés dans son Essai sur la constitution et l’origine du système solaire, 1873, (Acad. de Montpellier, Section des Sciences, t. viii, p. 235).
- ↑ E. Roche : Mémoire sur la figure des atmosphères des corps célestes, 1854 (Acad. de Montpellier, Section des Sciences, t. II, p. 399).
- ↑ M. Fouché : Comptes rendus de l’Académie des Sciences, 24 nov. 1884, t. 99, p. 903).
- ↑ Hirn : Mémoire sur les conditions d’équilibre et sur la nature probable des anneaux de Saturne, 1872.
- ↑ Maxwell : On the stability of the motion of Saturn’s rings, Cambridge, 1839, Maxwell’s Scientific Papers, t. I, p. 288-376. Voir aussi Tisserand : Traité de Mécanique Céleste, t. II, Chap. XII ; et H. Poincaré : Figures d’équilibre d’une masse fluide, Chap. VIII (Paris, Gauthier-Villars, 1900).
- ↑ Ces deux équations sont les mêmes, quel que soit l’indice i du satellite que l’on considère.
- ↑ Si, par exemple, le nombre des satellites est pair, p = 2q, il suffira de donner à les valeurs 1, 2, …, q. À chacune de ces valeurs correspondent 4 valeurs de soit en tout 4q valeurs de Or, pour chaque valeur de les formules (4) comportent deux arbitraires (savoir et un facteur constant). On obtient donc ainsi 8q = 4p constantes arbitraires, comme l’exige l’intégrale générale des équations (2).
- ↑ H. Poincaré : Sur l’équilibre d’une masse fluide animée d’un mouvement de rotation, 1885 (Bulletin astronomique, t. II, p. 117).
- ↑ E. Roche : Mémoire sur la figure d’une masse fluide soumise à l’attraction d’un point éloigné, 1849, 1850, 1851 (Acad. de Montpellier, Section des Sciences, t. I, p. 243 et 333, t. II, p. 21). Voir aussi Tisserand : Traité de Mécanique Céleste, t. II, Ch. VIII, p. 110.
- ↑ Je dis notablement, car est le rayon moyen de la nébuleuse ; or, celle-ci est allongée vers le Soleil, donc son plus grand rayon peut dépasser sensiblement .



















![{\displaystyle r={\sqrt[{3}]{\frac {\mathrm {M} }{\omega ^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/409c68b877d262bb4442971b7b7500aa7542eba3)











![{\displaystyle {\begin{array}{c}\mathrm {U} (x,y,0)=\mathrm {C} ,\\[0.75ex]{\dfrac {d\mathrm {U} }{dx}}=0,\qquad {\dfrac {d\mathrm {U} }{dy}}=0,\end{array}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38e11cda51a04d58de0fda3ff4d04f25fc6413b5)























































![{\displaystyle \left\{{\begin{aligned}-\left({\frac {d\mathrm {P} }{dx}}+{\frac {1}{\rho }}{\frac {dp}{dx}}\right)&={\frac {du}{dt}}\,+u{\frac {du}{dx}}\,+v{\frac {du}{dy}}\,+\,w{\frac {du}{dz}}-\gamma \Delta u,\\[0.5ex]-\left({\frac {d\mathrm {P} }{dy}}+{\frac {1}{\rho }}{\frac {dp}{dy}}\right)&={\frac {dv}{dt}}\;+u{\frac {dv}{dx}}\,+v{\frac {dv}{dy}}\,+\,w{\frac {dv}{dz}}-\gamma \Delta v,\\[0.5ex]-\left({\frac {d\mathrm {P} }{dz}}+{\frac {1}{\rho }}{\frac {dp}{dz}}\right)&={\frac {dw}{dt}}+u{\frac {dw}{dx}}+v{\frac {dw}{dy}}+w{\frac {dw}{dz}}-\gamma \Delta w,\\{\frac {d\rho }{dt}}&+{\frac {d}{dx}}(\rho u)+{\frac {d}{dy}}(\rho v)+{\frac {d}{dz}}(\rho w)=0\,;\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1668c99515414475b6f672f0c6a8a0e8b9da2dd6)
































































![{\displaystyle \left\{{\begin{aligned}{\frac {d^{2}r_{1}}{dt^{2}}}-r_{1}\left({\frac {d\nu _{1}}{dt}}\right)^{2}&=-{\frac {\mathrm {M} }{r_{1}^{2}}}+{\frac {d\mathrm {R} _{1}}{dr_{1}}},\\[0.75ex]r_{1}{\frac {d^{2}\nu _{1}}{dt^{2}}}+2{\frac {d\nu _{1}}{dt}}{\frac {dr_{1}}{dt}}&={\frac {1}{r_{1}}}{\frac {d\mathrm {R} _{1}}{d\nu _{1}}}\,;\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfcbfad1aba4efd2dfb05028a48d88618f63e3de)


![{\displaystyle \left\{{\begin{aligned}3\omega ^{2}\rho _{i}+2\omega \sigma _{i}'-\rho _{i}''&=-{\frac {1}{a^{2}}}{\frac {d(\delta \mathrm {R} _{i})}{d\rho _{i}}},\\[0.75ex]\sigma _{i}''+2\omega \rho _{i}'&={\frac {1}{a^{2}}}{\frac {d(\delta \mathrm {R} _{i})}{d\sigma _{i}}},\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/237a6c92fbd09266b2251c14fa60966c3da7149d)


![{\displaystyle \left\{{\begin{aligned}\rho _{i}&=\mathrm {H} _{i}e^{\mathrm {N} t},\\[0.5ex]\sigma _{i}&=\mathrm {K} _{i}e^{\mathrm {N} t}.\\\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8de03a4be29fb69593bf88591149cb183f4a7d7)




![{\displaystyle \left\{{\begin{aligned}\rho _{i}&=\mathrm {A} \cos \left(\alpha +2\gamma i\theta +nt\right),\\[0.5ex]\sigma _{i}&=\mathrm {B} \sin \left(\alpha +2\gamma i\theta +nt\right),\\\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b215b9b82c54fefb6c4bba0e01d6f52200c6619a)


![{\displaystyle {\begin{aligned}\omega ^{2}\mu \left[\mathrm {AL} _{\gamma }-\mathrm {BM} _{\gamma }\right]&\cos \left(\alpha +2\gamma i\theta +nt\right),\\\omega ^{2}\mu \left[\mathrm {AM} _{\gamma }+\mathrm {BN} _{\gamma }\right]&\sin \left(\alpha +2\gamma i\theta +nt\right),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6facc2ec6fb5c5159ade7e63dfb6ca9141af1e62)

![{\displaystyle \left\{{\begin{aligned}3\omega ^{2}\mathrm {A} +2\omega n\mathrm {B} +n^{2}\mathrm {A} &=\omega ^{2}\mu \left[\mathrm {AL} _{\gamma }-\mathrm {BM} _{\gamma }\right],\\-n^{2}\mathrm {B} -2\omega n\mathrm {A} &=\omega ^{2}\mu \left[\mathrm {AM} _{\gamma }+\mathrm {BN} _{\gamma }\right],\\\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/600c26862030999554f9a5ebf39bbdbb51d2aef5)

































![{\displaystyle \left\{{\begin{aligned}3\omega ^{2}\mathrm {A} +2\omega n\mathrm {B} +n^{2}\mathrm {A} &=0,\\[0.75ex]-n^{2}\mathrm {B} -2\omega n\mathrm {A} &=4\pi \mathrm {DB} \,;\\\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b8f22bf1448799b7a5801aa4a6b9fd72a8af149)





















![{\displaystyle \left\{{\begin{aligned}{\frac {d^{2}\left(\varphi -\mathrm {P} \right)}{dx^{2}}}&<0,\\[0.75ex]{\frac {d^{2}\left(\varphi -\mathrm {P} \right)}{dy^{2}}}&<0,\\[0.75ex]{\frac {d^{2}\left(\varphi -\mathrm {P} \right)}{dz^{2}}}&<0.\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/707cdb18213d686631a55402a6848be992632ca7)







![{\displaystyle {\begin{aligned}{\frac {d^{2}\varphi }{dx^{2}}}&=0,&{\frac {d^{2}\varphi }{dy^{2}}}&=\omega ^{2}+2\omega \omega 'y,&{\frac {d^{2}\varphi }{dz^{2}}}&=\omega ^{2}\,;\\[0.75ex]{\frac {d^{2}{\dfrac {\mathrm {M} }{r}}}{dx^{2}}}&=-{\frac {\mathrm {M} }{y^{4}}},&{\frac {d^{2}{\dfrac {\mathrm {M} }{r}}}{dy^{2}}}&={\frac {2\mathrm {M} }{y^{4}}},&{\frac {d^{2}{\dfrac {\mathrm {M} }{r}}}{dz^{2}}}&=-{\frac {\mathrm {M} }{y^{4}}}\,;\\[0.75ex]{\frac {d^{2}\!\left(\delta \mathrm {P} \right)}{dx^{2}}}&=-\varepsilon ,&{\frac {d^{2}\!\left(\delta \mathrm {P} \right)}{dy^{2}}}&=\varepsilon +\varepsilon '-4\pi \rho ,&{\frac {d^{2}\!\left(\delta \mathrm {P} \right)}{dz^{2}}}&=-\varepsilon '\,;\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7360fbe21c05ddda1cbf8d8a84b1812bfd2bdbd)












![{\displaystyle \left\{{\begin{aligned}4\pi \rho &<{\frac {\omega ^{2}}{14}},\\[0.75ex]4\pi \rho &>3\omega ^{2}+2\omega \omega '\mathrm {R} .\\\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f617475363b6c93e4ebfda490a0fc0671b62672)















![{\displaystyle {\begin{aligned}\omega &={\sqrt {\mathrm {M} }}\left(1+\varepsilon _{0}\right)^{\frac {1}{2}}\left(1+\varepsilon \right)^{-2}\\[0.5ex]&={\sqrt {\mathrm {M} }}\left(1+{\frac {\varepsilon _{0}}{2}}-2\varepsilon \right)\\[0.5ex]&={\sqrt {\mathrm {M} }}\left[1+\varepsilon _{0}\left({\frac {1}{2}}-2\lambda \right)\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a1693521eb1700facef21af06a3dc1ae1a73104)



























![{\displaystyle {\begin{aligned}\mathrm {Q} -\mathrm {P} s&={\frac {\omega ^{2}(s+3+\mu )}{1+\mu }},\\[0.5ex]\mathrm {R} -\mathrm {P} t&={\frac {\omega ^{2}(t+\mu )}{1+\mu }}\cdot \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bea8f692fab01ac52220495b57a23f4396b28f0)






![{\displaystyle {\begin{aligned}0<s&<1,\\[0.5ex]0<t&<1,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57f32e919d62e51ba5cca67b5354690a65cb33ca)







































![{\displaystyle {\frac {l}{r}}>2,44{\sqrt[{3}]{\frac {\delta }{\rho }}}\cdot }](https://wikimedia.org/api/rest_v1/media/math/render/svg/43179adea700900bed4f42a34e27e5a3d2325f31)



