Les méthodes nouvelles de la mécanique céleste/Chap.29

Henri Poincaré

Les méthodes nouvelles de la mécanique céleste

Gauthier-Villars, 1899 (3, p. 249-293).

CHAPITRE XXIX.

DIVERSES FORMES DU PRINCIPE DE MOINDRE ACTION.

---

336.Soient

${\begin{array}{llll}x_{1},&x_{2},&\ldots ,&x_{n},\\y_{1},&y_{2},&\ldots ,&y_{n}\end{array}}$

une double série de variables et $\mathrm {F}$ une fonction quelconque de ces variables. Considérons l’intégrale

$\mathrm {J} =\int _{t_{0}}^{t_{1}}\left(-\mathrm {F} +\sum y_{i}\,{\frac {dx_{i}}{dt}}\right)dt.$

La variation de cette intégrale peut s’écrire

$\delta \mathrm {J} =\int \left(-\delta \mathrm {F} +\sum \delta y_{i}\,{\frac {dx_{i}}{dt}}+\sum y_{i}\,{\frac {d\,\delta x_{i}}{dt}}\right)dt.$

Pour que cette variation s’annule, il faut d’abord que l’on ait

(1)

${\begin{aligned}{\frac {dx_{i}}{dt}}&={\frac {d\mathrm {F} }{dy_{i}}},&{\frac {dy_{i}}{dt}}&=-{\frac {d\mathrm {F} }{dx_{i}}},\end{aligned}}$

ce qui nous donne les équations canoniques, mais cette condition n’est pas suffisante. Si elle est remplie, on a

$\delta \mathrm {J} =\sum {\big [}y_{i}\,\delta x_{i}{\big ]}_{t=t_{0}}^{t=t_{1}}$

et il faut encore que le second membre de cette égalité soit nul. C’est ce qui arrive si l’on suppose que les $\delta x_{i}$ sont nuls aux deux limites, c’est-à-dire que les valeurs initiales et finales des $x_{i}$ sont données. Dans ces conditions, l’intégrale $\mathrm {J}$ qu’on appelle l’action est minimum.

Changeons de variables ; soient $x_{i}',\,y_{i}'$ les nouvelles variables et imaginons qu’elles aient été choisies de telle sorte que

(2)

$\sum y_{i}'\,dx_{i}'-\sum y_{i}\,dx_{i}=d\mathrm {S}$

soit une différentielle exacte. Dans ce cas nous avons vu que le changement de variables n’altère pas la forme canonique des équations et ce résultat est d’ailleurs une conséquence immédiate des diverses propositions qui vont suivre ; soit alors

$\mathrm {J} '=\int _{t_{0}}^{t_{1}}\left(-\mathrm {F} +\sum y_{i}'\,{\frac {dx_{i}'}{dt}}\right)dt.$

On a

$\mathrm {J} '-\mathrm {J} =\int {\frac {d\mathrm {S} }{dt}}\,dt=\mathrm {S} _{1}-\mathrm {S} _{0},$

$\mathrm {S} _{0}$ et $\mathrm {S} _{1}$ étant les valeurs de la fonction $\mathrm {S}$ pour $t=t_{0}$ et $t=t_{1}.$

On a donc

(3)

$\delta \mathrm {J} '=\delta \mathrm {J} +{\big [}\delta \mathrm {S} {\big ]}_{t=t_{0}}^{t=t_{1}}$

Si les équations canoniques (1) sont satisfaites, on a

(4)

$\delta \mathrm {J} =+{\big [}y_{i}\,\delta x_{i}{\big ]}_{t=t_{0}}^{t=t_{1}},$

et, par conséquent, en vertu de (2) et de (3),

(4 bis)

$\delta \mathrm {J} '=+{\big [}y_{i}'\,\delta x_{i}'{\big ]}_{t=t_{0}}^{t=t_{1}},$

Mais, de même que la relation (4) est équivalente aux équations (1), la relation (4 bis) est équivalente aux équations

(1 bis)

${\begin{aligned}{\frac {dx_{i}}{dt}}&={\frac {d\mathrm {F} }{dy_{i}}},&{\frac {dy_{i}}{dt}}&=-{\frac {d\mathrm {F} }{dx_{i}}}\cdot \end{aligned}}$

Or, nous venons de voir que (4) équivaut à (4 bis) ; les équations (1) sont équivalentes aux équations (1 bis), ce qui veut dire, comme nous le savions déjà, que le changement de variables n’altère pas la forme canonique des équations.

Alors l’action $\mathrm {J} '$ sera minimum quand on supposera que les valeurs initiales et finales des variables $x_{i}'$ sont données. À chaque système de variables canoniques correspond donc une forme nouvelle du principe de moindre action.

Les équations (1) entraînent l’intégrale des forces vives

(5)

$\mathrm {F} =h$

où $h$ est une constante.

Nous avons supposé jusqu’à présent que les deux limites $t_{0}$ et $t_{1}$ sont données ; qu’arrive-t-il si les limites sont regardées comme variables. Comme $\mathrm {F}$ ne dépend pas explicitement du temps, nous ne restreindrons pas la généralité en supposant que $t_{0}$ est constant et en donnant seulement à $t_{1}$ un accroissement $\delta t_{1}.$ Supposons, par exemple, $t_{0}=0$ et imaginons qu’après la variation les variables $x_{i}$ et $y_{i}$ aient à l’époque ${\frac {t}{t_{1}}}(t_{1}+\delta t_{1})$ les mêmes valeurs qu’elles avaient à l’époque $t$ avant la variation.

On aura, avant la variation,

$\mathrm {J} =-ht_{1}+\sum \int y_{i}{\frac {dx_{i}}{dt}}\,dt.$

Mais

$\int y_{i}{\frac {dx_{i}}{dt}}\,dt=\int y_{i}\,dx_{i}$

ne dépend pas du temps ; sa variation est donc nulle. On a donc simplement

$\delta \mathrm {J} =-h\,\delta t_{1}.$

La dérivée de l’action $\mathrm {J}$ par rapport à la limite supérieure d’intégration $t_{1}$ est donc égale à la constante de l’énergie $h$ changée de signe.

Si cette constante est nulle, l’action $\mathrm {J}$ est encore minimum, si l’on regarde les valeurs initiales et finales des variables $x_{i}$ comme données et quand même on ne regarderait pas comme données les valeurs initiale et finale du temps, $t_{0}$ et $t_{1}.$

Si l’on change $\mathrm {F}$ en $\mathrm {F} -h,$ $\mathrm {J}$ se change en

(6)

$\mathrm {J} +h(t_{1}-t_{0})\,;$

comme les équations (1) ne changent pas, cette expression (6) est encore minimum.

Mais, si l’on change $\mathrm {F}$ en $\mathrm {F} -h,$ la constante des forces vives, qui était égale à $h,$ devient nulle ; par conséquent, l’expression (6) est minimum, même si l’on ne regarde pas $t_{1}$ et $t_{0}$ comme donnés.

L’action $\mathrm {J}$ est minimum quelles que soient les variables $x_{i}$ et $y_{i}\,;$ elle sera donc minimum a fortiori si nous lui imposons une condition nouvelle compatible avec les équations (1).

Imposons-lui, par exemple, la condition de satisfaire à la première série des équations (1), c’est-à-dire à

${\frac {dx_{i}}{dt}}={\frac {d\mathrm {F} }{dy_{i}}},$

d’où

$\mathrm {J} =\int _{t_{0}}^{t_{1}}\left(-\mathrm {F} +\sum y_{i}\,{\frac {d\mathrm {F} }{dy_{i}}}\right)dt=\int _{t_{0}}^{t_{1}}\mathrm {H} \,dt,$

en posant

$\mathrm {H} =-\mathrm {F} +\sum y_{i}\,{\frac {d\mathrm {F} }{dy_{i}}}\cdot$

L’action $\mathrm {J} ,$ ainsi définie, est minimum.

C’est le principe de moindre action mis sous sa forme hamiltonienne.

Supposons maintenant

$h=0.$

Ne regardons donc plus les variables $x_{i}$ et $y_{i}$ comme indépendantes, mais imposons-leur la condition

$\mathrm {F} =0.$

Cette restriction, compatible avec les équations (1), n’empêchera pas l’action $\mathrm {J}$ d’être minimum.

Alors

$\mathrm {J} =\int \sum y_{i}\,{\frac {dx_{i}}{dt}}\,dt$

et, comme $h$ est nul, cette intégrale est minimum quand même on ne regarde pas $t_{1}$ et $t_{0}$ comme donnés.

Imposons-nous alors les conditions

${\frac {dx_{i}}{dt}}={\frac {d\mathrm {F} }{dy_{i}}},$

d’où nous tirons les $y_{i}$ en fonction des ${\frac {dx_{i}}{dt}},$

$y_{i}=\varphi _{i}\!\left(x_{1},x_{2},\ldots ,x_{n},{\frac {dx_{1}}{dt}},{\frac {dx_{2}}{dt}},\ldots ,{\frac {dx_{n}}{dt}}\right)$

ou encore

(7)

$\;y_{i}=\varphi _{i}\!\left(\!x_{1},x_{2},\ldots ,x_{n},{\frac {dx_{1}}{dt}},{\frac {dx_{2}}{dx_{1}}}{\frac {dx_{1}}{dt}},{\frac {dx_{3}}{dx_{1}}}{\frac {dx_{1}}{dt}},\ldots ,{\frac {dx_{n}}{dx_{1}}}{\frac {dx_{1}}{dt}}\!\right).$

Substituons, à la place des $y_{i},$ leurs valeurs (7) dans $\mathrm {J}$ et dans l’équation

$\mathrm {F} =0.$

De cette équation, nous tirerons ${\frac {dx_{1}}{dt}}$ en fonction des $x_{k}$ et des ${\frac {dx_{k}}{dx_{1}}}\cdot$ Nous substituerons ensuite cette valeur de ${\frac {dx_{1}}{dt}}$ dans les expressions (7) et dans $\mathrm {J} \,;$ cette dernière intégrale prendra la forme

$\int \sum y_{i}\,{\frac {dx_{i}}{dx_{1}}}\,dx_{1}=\int \Phi \,dx_{1},$

où $\Phi$ est fonction des $x_{k}$ et des dérivées ${\frac {dx_{k}}{dx_{1}}}\cdot$ Cette intégrale, mise ainsi sous une forme indépendante du temps, est encore minimum. C’est là le principe de moindre action sous sa forme maupertuisienne.

Si $h$ n’était pas nul, on n’aurait qu’à changer $\mathrm {F}$ en $\mathrm {F} -h.$

337.Examinons d’abord le cas particulier le plus important.

Supposons que l’on ait

$\mathrm {F} =\mathrm {T} -\mathrm {U} ,$

$\mathrm {T}$ étant homogène du second degré par rapport aux variables $y_{i},$ tandis que $\mathrm {U}$ est indépendant de ces variables.

Il vient alors

${\begin{aligned}\sum y_{i}\,{\frac {d\mathrm {F} }{dy_{i}}}&=2\mathrm {T} ,&\mathrm {H} &=\mathrm {T} +\mathrm {U} .\end{aligned}}$

D’après le principe de Hamilton, l’intégrale

$\int _{t_{0}}^{t_{1}}\left(\mathrm {T} +\mathrm {U} \right)\,dt$

doit être minimum.

Voyons ce que devient le principe de Maupertuis ; l’équation des forces vives s’écrit

$\mathrm {T} -\mathrm {U} =h.$

Alors, l’action maupertuisienne a pour expression

$\int \left(\mathrm {T} +\mathrm {U} +h\right)\,dt.$

Les équations

${\frac {dx_{i}}{dt}}={\frac {d\mathrm {F} }{dy_{i}}}={\frac {d\mathrm {T} }{dy_{i}}}$

ont leurs seconds membres linéaires et homogènes par rapport aux $y_{i}\,;$ donc $\mathrm {T}$ est homogène du second degré par rapport aux ${\frac {dx_{i}}{dt}}\,;$ soit alors $d\tau ^{2}$ ce que devient $\mathrm {T}$ quand on y remplace ${\frac {dx_{i}}{dt}}$ par $dx_{i},$ on aura

$\mathrm {T} ={\frac {d\tau ^{2}}{dt^{2}}}$

et $d\tau ^{2}$ sera une forme linéaire et homogène par rapport aux $n$ différentielles $dx_{i}\,;$ on déduit de là

$dt={\frac {d\tau }{\sqrt {\mathrm {T} }}}={\frac {d\tau }{\sqrt {\mathrm {U} +h}}}\cdot$

L’action maupertuisienne aura alors pour expression

$2\int d\tau \,{\sqrt {\mathrm {U} +h}}.$

338.Pour pouvoir étudier d’autres cas particuliers, posons, pour abréger,

$x_{i}'={\frac {dx_{i}}{dt}}\,;$

tirons les $y_{i}$ des équations

$x_{i}'={\frac {d\mathrm {F} }{dy_{i}}},$

de façon à prendre pour variables nouvelles les $x_{i}$ et les $x_{i}'\,;$ désignons par des $d$ ordinaires les dérivées prises par rapport aux $x_{i}$ et aux $y_{i}$ et par des $\partial \,$ ronds les dérivées prises par rapport aux $x_{i}$ et aux $x_{i}'.$

On trouverait facilement les relations bien connues

${\begin{aligned}y_{i}={\frac {\partial \mathrm {H} }{dx_{i}'}},\qquad {\frac {\partial \mathrm {H} }{dx_{i}}}&=-{\frac {\partial \mathrm {F} }{dx_{i}}},\\\mathrm {F} =\sum x_{i}'\,{\frac {\partial \mathrm {H} }{dx_{i}'}}&-\mathrm {H} \end{aligned}}$

et l’on verrait que les équations (1) sont équivalentes aux équations de Lagrange,

${\frac {d}{dt}}{\frac {\partial \mathrm {H} }{\partial x_{i}'}}={\frac {\partial \mathrm {H} }{dx_{i}}}\cdot$

Cela posé, examinons le cas où $\mathrm {H}$ est de la forme suivante

$\mathrm {H} =\mathrm {H} _{0}+\mathrm {H} _{1}+\mathrm {H} _{2},$

$\mathrm {H} _{0},\,\mathrm {H} _{1},\,\mathrm {H} _{2}$ étant homogènes, respectivement de degré 0, 1, 2 par rapport aux variables $x_{i}'.$

On a alors

${\begin{aligned}\sum x_{i}'{\frac {\partial \mathrm {H} }{\partial x_{i}'}}&=2\mathrm {H} _{2}+\mathrm {H} _{1},\\[0.75ex]\mathrm {F} &=\mathrm {H} _{2}-\mathrm {H} _{0}\end{aligned}}$

et les

$y_{i}={\frac {\partial \mathrm {H} _{2}}{\partial x_{i}'}}+{\frac {\partial \mathrm {H} _{1}}{\partial x_{i}'}}$

sont des fonctions linéaires, mais non homogènes par rapport aux $x_{i}'.$

L’action hamiltonienne conserve la même forme

$\int \mathrm {H} \,dt.$

Voyons ce que devient l’action maupertuisienne.

Soit $h$ la constante des forces vives ; l’action maupertuisienne aura pour expression

$\int \left(\mathrm {H} +h\right)\,dt\,;$

mais il faut la mettre sous une forme indépendante du temps.

Pour cela, posons

$\mathrm {H} _{2}={\frac {d\tau ^{2}}{dt^{2}}},$

et

$\mathrm {H} _{1}={\frac {d\sigma }{dt}}\cdot$

$\mathrm {H} _{2}$ n’est autre chose que la force vive, et $d\tau ^{2}$ est ce que devient cette force vive quand on y remplace $x_{i}'$ par $dx_{i}.$ De même $d\sigma$ est ce que devient $\mathrm {H} _{1}$ quand on y remplace $x_{i}'$ par $dx_{i}\,;$ c’est donc une forme linéaire homogène par rapport aux différentielles $dx_{i}.$

Si l’on tient compte de l’équation des forces vives

$\mathrm {H} _{2}=\mathrm {H} _{0}+h,$

d’où

$dt={\frac {d\tau }{\sqrt {\mathrm {H} _{0}+h}}}$

l’action maupertuisienne deviendra

$\int \left[2\,d\tau \,{\sqrt {\mathrm {H} _{0}+h}}+d\sigma \right].$

Le principe de Maupertuis est donc applicable au cas qui nous occupe, comme à celui du mouvement absolu ; mais il y a une différence essentielle au point de vue de ce qui va suivre.

Dans tous les problèmes que l’on rencontrera, la force vive $\mathrm {T}$ ou $\mathrm {H} _{2}$ est essentiellement positive ; c’est une forme quadratique définie positive. Dans le cas du mouvement absolu (n^o 337) l’action

$\int 2\,d\tau \,{\sqrt {\mathrm {U} -h}}$

est essentiellement positive ; elle ne change pas quand on permute les limites. Au contraire, dans le cas actuel, l’action se compose de deux termes ; le premier

$\int 2\,d\tau \,{\sqrt {\mathrm {H} _{0}+h}}$

est toujours positif et ne change pas quand on permute les limites.

Le second, $\textstyle \int d\sigma ,$ change de signe quand on permute les limites ; il peut donc être positif ou négatif.

Si l’on observe de plus que, dans certains cas, le premier terme s’annule sans que le second s’annule, on verra que l’action n’est pas toujours positive et cette circonstance nous occasionnera dans la suite beaucoup de difficultés.

339.Pour montrer comment les considérations qui précèdent s’appliquent au mouvement relatif, considérons d’abord le mouvement absolu du système ; soit donc

$\mathrm {H} =\mathrm {T} +\mathrm {U}$

et imaginons que la position du système soit définie par $n+1$ variables

$x_{1},\quad x_{2},\quad \ldots ,\quad x_{n},\quad \omega ,$

où $x_{1},\,x_{2},\,\ldots ,\,x_{n}$ suffisent pour définir la position relative des différents points du système, et $\omega$ l’orientation du système dans l’espace.

Si le système est isolé, $\mathrm {U}$ dépendra seulement de $x_{1},$ $x_{2},\,\ldots ,$ $x_{n}\,;$ $\mathrm {T}$ sera une forme quadratique homogène par rapport à $x_{1}',$ $x_{2}',\,\ldots ,$ $x_{n}',$ $\omega '$ dont les coefficients dépendent seulement de $x_{1},$ $x_{2},\,\ldots ,\,x_{n}.$

On aura alors l’équation

${\frac {d\mathrm {T} }{d\omega '}}=p,$

où $p$ est une constante ; c’est l’intégrale des aires.

Cela posé, soit $\mathrm {J}$ l’action hamiltonienne

$\mathrm {J} =\int _{t_{0}}^{t_{1}}\mathrm {H} \,dt\,;$

on aura, si les équations du mouvement sont satisfaites,

$\delta \mathrm {J} =\left[\sum {\frac {d\mathrm {T} }{dx_{i}'}}\,\delta x_{i}+{\frac {d\mathrm {T} }{d\omega '}}\,\delta \omega \right]_{t=t_{0}}^{t=t_{1}}.$

L’action sera minimum (ou plutôt sa première variation sera nulle) si les valeurs initiales et finales des $x_{i}$ et de $\omega$ sont regardées comme données, c’est-à-dire si $\delta x_{i}=\delta \omega =0$ pour $t=t_{0}$ et pour $t=t_{1}.$

Supposons maintenant que nous regardions comme données les valeurs initiales et finales des $x_{i},$ mais pas celles de $\omega \,;$ nous aurons

$\delta \mathrm {J} ={\big [}p\,\delta \omega {\big ]}_{t=t_{0}}^{t=t_{1}}=p\,{\big [}\delta \omega {\big ]}_{t=t_{0}}^{t=t_{1}}.$

Soit alors

$\mathrm {H} '=\mathrm {H} -p\omega '$

et

$\mathrm {J} '=\int \mathrm {H} '\,dt,$

il viendra évidemment

$\delta \mathrm {J} '=0.$

De l’équation ${\frac {d\mathrm {T} }{d\omega '}}=p,$ on tire $\omega '$ qui est une fonction linéaire non homogène des $x'_{i}\,;$ on voit ainsi que $\mathrm {H} '$ est une fonction quadratique non homogène par rapport aux $x_{i}'.$

$\mathrm {H} '$ est donc de la forme $\mathrm {H} _{0}+\mathrm {H} _{1}+\mathrm {H} _{2},$ étudiée au n^o 338.

Ainsi l’intégrale $\mathrm {J} '$ sera minimum, alors même que les valeurs initiale et finale de w ne sont pas regardées comme données.

On a d’ailleurs

$\mathrm {J} '=\mathrm {J} -p(\omega _{1}-\omega _{0}),$

$\omega _{0}$ et $\omega _{1}$ étant les valeurs de $\omega$ pour $t=t_{0}$ et $t=t_{1}.$

340.Supposons maintenant un système rapporté à des axes mobiles, et soumis à des forces qui ne dépendent que de la situation relative du système par rapport aux axes mobiles. Supposons de plus que les axes soient animés d’un mouvement de rotation uniforme de vitesse angulaire constante $\omega '.$

e problème se ramène immédiatement au précédent ; nous n’avons qu’à attribuer aux axes mobiles un moment d’inertie très grand de telle façon que sa vitesse angulaire demeure constante.

On a alors pour le mouvement absolu

$\mathrm {H} =\mathrm {T} +\mathrm {U} =\mathrm {T} _{1}+\mathrm {T} _{2}+\mathrm {U} .$

La fonction des forces $\mathrm {U}$ ne dépend que des variables $x_{i}$ qui définissent la position du système par rapport aux axes mobiles ; $\mathrm {T} _{1},$ force vive du système, dépend des $x_{i}$ et est une forme quadratique par rapport aux $x_{i}'$ et à $\omega '\,;$ $\mathrm {T} _{2},$ force vive des axes mobiles, est égal à

${\frac {\mathrm {I} }{2}}\,\omega '^{2}$

et le moment d’inertie $\mathrm {I}$ est très grand.

Il vient alors

$p={\frac {d\mathrm {T} _{1}}{d\omega '}}+\mathrm {I} \,\omega '$

et

$\mathrm {H} '=\mathrm {H} -p\omega '=(\mathrm {T} _{1}+\mathrm {T} _{2}+\mathrm {U} )-{\frac {d\mathrm {T} _{1}}{d\omega '}}\,\omega '-\mathrm {I} \,\omega '^{2}$

ou

$\mathrm {H} '=\mathrm {T} _{1}+\mathrm {U} -{\frac {d\mathrm {T} _{1}}{d\omega '}}\,\omega '-{\frac {\mathrm {I} \,\omega '^{2}}{2}}\cdot$

Or,

$\mathrm {I} \omega '=p-{\frac {d\mathrm {T} _{1}}{d\omega '}}\cdot$

Comme $\mathrm {I}$ et $p$ sont très grands par rapport à ${\frac {d\mathrm {T} _{1}}{d\omega '}},$ cette équation nous donne approximativement

$\omega '={\frac {p}{\mathrm {I} }}$

et plus exactement

$\omega '={\frac {p}{\mathrm {I} }}-{\frac {1}{\mathrm {I} }}{\frac {d\mathrm {T} _{1}}{d\omega '}}\cdot$

De plus

${\frac {\mathrm {I} \omega '^{2}}{2}}={\frac {p^{2}}{2\mathrm {I} }}-{\dfrac {p\,{\frac {d\mathrm {T} _{1}}{d\omega '}}}{\mathrm {I} }}+{\frac {1}{2\mathrm {I} }}\left({\frac {d\mathrm {T} _{1}}{d\omega '}}\right)^{2}\cdot$

On trouve ainsi

$\mathrm {H} ''=\mathrm {T} _{1}+\mathrm {U} -{\frac {p^{2}}{2\mathrm {I} }}+{\frac {1}{2\mathrm {I} }}\left({\frac {d\mathrm {T} _{1}}{d\omega '}}\right)^{2}\cdot$

Dans le second membre, l’avant-dernier terme est une constante ; le dernier est négligeable parce que $\mathrm {I}$ est très grand.

Comme on peut, sans rien changer au principe de Hamilton, ajouter à $\mathrm {H} '$ une constante quelconque, nous pourrons poser

$\mathrm {H} '=\mathrm {T} _{1}+\mathrm {U}$

et nous saurons que l’intégrale

$\mathrm {J} ''=\int \mathrm {H} ''\,dt$

doit être minimum (alors même que les valeurs initiale et finale de $\omega$ ne sont pas données).

Dans l’expression de $\mathrm {H} '',$ $\omega '$ doit être regardée comme une constante donnée ; $\mathrm {H} ''$ est alors une fonction quadratique, non homogène par rapport aux $x_{i}',$ de la forme $\mathrm {H} _{0}+\mathrm {H} _{1}+\mathrm {H} _{2}.$

Soit, par exemple, un point matériel de masse 1 se mouvant dans un plan et dont les coordonnées par rapport aux axes mobiles sont $\xi$ et $\eta .$ On aura

$\mathrm {T} _{1}={\frac {(\xi '\!-\omega '\eta )^{2}+(\eta '\!-\omega '\xi )^{2}}{2}}\cdot$

Il viendra donc

${\begin{aligned}\mathrm {H} _{2}&={\frac {\xi '^{2}\!+\eta '^{2}}{2}},&\mathrm {H} _{1}&=\omega '(\xi \eta '\!-\xi '\eta ),&\mathrm {H} _{0}&={\frac {\omega '^{2}}{2}}(\xi ^{2}\!+\eta ^{2})+\mathrm {U} .\end{aligned}}$

L’intégrale

$\mathrm {J} =\int _{t_{0}}^{t_{1}}(\mathrm {H} _{2}+\mathrm {H} _{1}+\mathrm {H} _{0})\,dt$

est alors minimum, quand on regarde comme données les limites $t_{0}$ et $t_{1}$ ainsi que les valeurs initiales et finales de $\xi$ et de $\eta .$

L’intégrale des forces vives s’écrit alors

$\mathrm {H} _{2}=\mathrm {H} _{0}+h$

et nous avons vu que l’intégrale

$\mathrm {J} '=\int (\mathrm {H} _{2}+\mathrm {H} _{1}+\mathrm {H} _{0}+h)\,dt=\mathrm {J} +h(t_{1}-t_{0})$

est minimum lors même qu’on ne regarde pas $t_{0}$ et $t_{1}$ comme donnés.

On trouve alors

$\mathrm {J} '=\int (2\mathrm {H} _{2}+\mathrm {H} _{1})dt=\int \left[ds\,{\sqrt {\mathrm {H} _{0}+h}}+\omega '(\xi \,d\eta -\nu \,d\xi )\right]$

en posant

$ds^{2}=d\xi ^{2}+d\eta ^{2}.$

C’est le principe de Maupertuis généralisé.

Dans les problèmes que nous traiterons, $\mathrm {U}$ sera toujours positif, et, par conséquent, $\mathrm {J}$ sera essentiellement positif.

Il n’en sera pas toujours de même de $\mathrm {J} '.$ En effet, si $h$ est négatif, nous devrons supposer que le point $\xi ,\,\eta$ reste cantonné dans le domaine défini par l’inégalité

$\mathrm {H} _{0}+h>0.$

Le premier terme de la quantité sous le signe $\textstyle \int$ qui est $ds\,{\sqrt {\mathrm {H} _{0}+h}}$ est essentiellement positif ; il n’en sera pas ainsi du second qui change de signe quand on renverse le sens dans lequel la trajectoire est supposée parcourue.

Si le point $\xi ,\,\eta$ est très voisin du bord du domaine où il est confiné, si, par conséquent, $\mathrm {H} _{0}+h$ est très petit, le premier terme sera très petit et ce sera le second qui donnera son signe.

$\mathrm {J} '$ n’est donc pas essentiellement positif. On s’en rend compte aussi à l’aide de l’équation

$\mathrm {J} '=\mathrm {J} +h(t_{1}-t_{0}).$

Si $h$ est négatif, le premier terme $\mathrm {J}$ est positif et le second négatif.

Foyers cinétiques.

341.Jusqu’ici quand j’ai dit, telle intégrale est minimum, je me suis servi d’une façon de parler abrégée, mais incorrecte, qui ne pouvait d’ailleurs tromper personne ; je voulais dire, la variation première de cette intégrale est nulle ; cette condition est nécessaire pour qu’il y ait minimum, mais elle n’est pas suffisante.

Nous allons maintenant rechercher quelle est la condition pour que les intégrales $\mathrm {J}$ et $\mathrm {J} ',$ que nous avons étudiées dans les numéros précédents, et dont les variations premières sont nulles, soient effectivement minimum. Cette recherche se rattache à la difficile question des variations secondes et à la belle théorie des foyers cinétiques.

Rappelons les principes de ces théories.

Soient $x_{1},\,x_{2},\,\ldots ,\,x_{n}$ des fonctions de $t\,;$ soient $x_{1}',$ $x_{2}',\,\ldots ,$ $x_{n}'$ leurs dérivées ; considérons l’intégrale

$\mathrm {J} =\int _{t_{0}}^{t_{1}}f(x_{i},x_{i}')\,dt,$

dont la variation première $\delta \mathrm {J}$ est nulle, en regardant comme données les valeurs initiales et finales des $x_{i}.$

Pour que cette intégrale soit minimum, il faut d’abord une condition, nécessaire, mais non suffisante, que j’appellerai la condition (A).

C’est que

$f(x_{i},\,x_{i}'+\varepsilon _{i})-\sum \varepsilon _{i}{\frac {df}{dx_{i}'}},$

considéré comme fonction des $\varepsilon _{i},$ soit minimum.

La condition (A) n’est pas suffisante, à moins que les limites d’intégration ne soient très rapprochées. Sauf ce cas, il faut y joindre une autre condition que j’appellerai la condition (B). Pour l’exposer, il faut d’abord que je rappelle la définition des foyers cinétiques.

Pour que

$\delta \mathrm {J} =0,$

il faut et il suffit que les $x_{i}$ satisfassent à $n$ équations différentielles du deuxième ordre que j’appellerai les équations (C).

Soit

$x_{i}=\varphi _{i}(t)$

une solution de ces équations.

Posons, pour une solution infiniment voisine

$x_{i}=\varphi _{i}(t)+\xi _{i},$

et formons les équations aux variations, équations linéaires auxquelles satisfont les $\xi _{i}$ et que j’appellerai (D).

La solution générale de ces équations (D) sera de la forme

$\xi _{i}=\sum _{k=1}^{k=2n}\mathrm {A} _{k}\xi _{ik}\quad (i=1,\,2,\,\ldots ,\,n).$

Les $\mathrm {A} _{k}$ sont $2n$ constantes d’intégration, les $\xi _{ik}$ sont $2n^{2}$ fonctions de $t,$ parfaitement déterminées et correspondant à $2n$ solutions particulières des équations linéaires (D).

Cela posé, écrivons que les $\xi _{i}$ s’annulent tous pour deux époques données $t=t',$ et pour $t=t''\,;$ nous aurons $2n$ équations linéaires entre lesquelles nous pourrons éliminer les $2n$ inconnues $\mathrm {A} _{k}.$

Nous obtiendrons ainsi l’équation

$\Delta (t',t'')=0,$

où $\Delta$ est le déterminant

$\Delta =\left|{\begin{array}{cccc}\xi _{1.1}'&\xi _{1.2}'&\ldots &\xi _{1.2n}'\\\ldots &\ldots &\ldots &\ldots .\\\xi _{n.1}'&\xi _{n.2}'&\ldots &\xi _{n.2n}'\\\xi _{1.1}''&\xi _{1.2}''&\ldots &\xi _{1.2n}''\\\ldots &\ldots &\ldots &\ldots .\\\xi _{n.1}''&\xi _{n.2}''&\ldots &\xi _{n.2n}''\end{array}}\right|\,;$

$\xi _{ik}'$ et $\xi _{ik}''$ sont ce que devient la fonction $\xi _{ik}$ quand on y remplace $t$ par $t'$ et par $t''.$

Si les époques $l'$ et $t''$ satisfont à l’équation $\Delta =0,$ nous dirons que ce sont deux époques conjuguées et que les deux points $\mathrm {M} '$ et $\mathrm {M} ''$ de l’espace à $n$ dimensions, qui ont respectivement pour coordonnées

${\begin{array}{cccc}\varphi _{1}(t'),&\varphi _{2}(t'),&\ldots ,&\varphi _{n}(t'),\\\varphi _{1}(t''),&\varphi _{2}(t''),&\ldots ,&\varphi _{n}(t''),\end{array}}$

sont deux points conjugués.

Si de plus $t''$ est celle des époques conjuguées de $t',$ et postérieure à $t',$ qui est la plus voisine de $t',$ nous dirons que $\mathrm {M} ''$ est le foyer de $\mathrm {M} '.$

Nous pouvons maintenant énoncer la condition (B) : c’est qu’entre $t_{0}$ et $t_{1}$ ne se trouve aucune époque conjuguée de $t_{0}.$

Pour que $\mathrm {J}$ soit un minimum, il faut et il suffit que les conditions (A) et (B) soient remplies.

On peut tirer de là une conséquence immédiate.

Soient $t_{0},\,t_{1},\,t_{2},\,t_{3}$ quatre époques.

Soient $\mathrm {M} _{0},\,\mathrm {M} _{1},\,\mathrm {M} _{2},\,\mathrm {M} _{3}$ les points correspondants de la courbe

$x_{1}=\varphi _{1}(t),\quad x_{2}=\varphi _{2}(t),\quad \ldots ,\quad x_{n}=\varphi _{n}(t).$

Supposons que $\mathrm {M} _{1}$ soit le foyer de $\mathrm {M} _{0}$ et $\mathrm {M} _{3}$ celui de $\mathrm {M} _{2}.$

Si la condition (A) est remplie on pourra avoir

$t_{0}<t_{1}<t_{2}<t_{3}$

ou

$t_{0}<t_{2}<t_{1}<t_{3}$

ou

$t_{2}<t_{3}<t_{0}<t_{1}.$

Mais on ne pourra pas avoir

$t_{0}<t_{2}<t_{3}<t_{1}\,;$

sans quoi l’intégrale

$\int _{t_{0}}^{t_{1}-\varepsilon }$

devrait être minimum puisque la condition (B) est remplie, et l’intégrale

$\int _{t_{3}}^{t_{1}-\varepsilon }$

ne serait pas minimum puisque la condition (B) ne serait pas remplie en ce qui la concerne.

Cela est impossible puisqu’on peut faire varier les fonctions $x_{i}$ entre $t_{2}$ et $t_{1}-\varepsilon ,$ sans les faire varier entre $t_{0}$ et $t_{2}.$

Il est aisé de voir quelle est la signification géométrique de ce qui précède.

La courbe de l’espace à $n$ dimensions

$x_{i}=\varphi _{i}(t)$

représentant une solution des équations (c) pourra s’appeler une trajectoire, que j’appelle $(\mathrm {T} ).$

La courbe

$x_{i}=\varphi _{i}+\xi _{i}$

représentera une trajectoire infiniment voisine.

Si par le point $\mathrm {M} '$ on mène une de ces trajectoires $(\mathrm {T} ')$ infiniment voisines de $(\mathrm {T} )$ et que cette trajectoire vienne de nouveau couper la trajectoire $(\mathrm {T} )$ en $\mathrm {M} ''$ (plus exactement, la distance de $\mathrm {M} ''$ à cette trajectoire sera un infiniment petit d’ordre supérieur) ; les points $\mathrm {M} '$ et $\mathrm {M} ''$ seront conjugués si, de plus, le point qui décrit $(\mathrm {T} ')$ passe en $\mathrm {M} '$ et infiniment près de $\mathrm {M} ''$ aux époques $t'$ et $t''.$

342.Dans le cas du principe de Hamilton, la condition (A) est toujours remplie ; en effet, on a

$\mathrm {H} =\mathrm {H} _{0}+\mathrm {H} _{1}+\mathrm {H} _{2},$

et $\mathrm {H} _{2}$ est une forme quadratique homogène par rapport aux $x_{i}'.$

Dans tous les problèmes de Dynamique, cette forme quadratique est définie et positive.

Si nous changeons $x_{i}'$ en $x_{i}+\varepsilon _{i},$ $H_{1}$ se change en

$\mathrm {H} _{1}(x_{i}')+\sum \varepsilon _{i}\,{\frac {d\mathrm {H} _{1}}{dx_{i}'}}$

et $\mathrm {H} _{2}$ se change en

$\mathrm {H} _{2}(x_{i}')+\mathrm {H} _{2}(\varepsilon _{i})+\sum \varepsilon _{i}\,{\frac {d\mathrm {H} _{2}}{dx_{i}'}}\,;$

d’ailleurs

$\sum \varepsilon _{i}\,{\frac {d\mathrm {H} _{0}}{dx_{i}'}}=0.$

Donc

$\mathrm {H} (x_{i}'+\varepsilon _{i})=\mathrm {H} _{0}+\mathrm {H} _{1}+\mathrm {H} _{2}+\sum \varepsilon _{i}{\frac {d(\mathrm {H} _{0}+\mathrm {H} _{1}+\mathrm {H} _{2})}{dx_{i}'}}+\mathrm {H} _{2}(\varepsilon _{i}).$

d’où enfin

$\mathrm {H} (x_{i}'+\varepsilon _{i})-\sum \varepsilon _{i}{\frac {d\mathrm {H} }{dx_{i}'}}=\mathrm {H} +\mathrm {H} _{2}(\varepsilon _{i}).$

Le premier membre correspond à la fonction

$f(x_{i}'+\varepsilon _{i})-\sum \varepsilon _{i}{\frac {df}{dx_{i}'}}\,;$

comme la forme quadratique $\mathrm {H} _{2}(\varepsilon _{i})$ est définie positive, nous voyons que l’expression est minimum pour $\varepsilon _{i}=0,$ c’est-à-dire que la condition (A) est remplie.

343.Passons au cas du principe de Maupertuis dans le mouvement absolu. L’intégrale à examiner s’écrit alors

$\int d\tau ,$

où $d\tau ^{2}$ est une forme quadratique définie positive par rapport aux différentielles $dx_{i}.$

Prenons pour un instant $x_{1}$ pour variable indépendante ; l’intégrale devient

$\int {\frac {d\tau }{dx_{1}}}\,dx_{1},$

où $\left({\frac {d\tau }{dx_{1}}}\right)^{2}$ est un polynôme du second degré $\mathrm {P}$ non homogène (mais essentiellement positif), par rapport aux ${\frac {dx_{i}}{dx_{1}}}\cdot$ Soit donc

${\frac {d\tau }{dx_{1}}}={\sqrt {\mathrm {P} \left({\frac {dx_{i}}{dx_{1}}}\right)}}\cdot$

Il s’agit de savoir si

${\sqrt {\mathrm {P} \left({\frac {dx_{i}}{dx_{1}}}+\varepsilon _{i}\right)}}-\sum \varepsilon _{i}\;{\frac {d}{dx_{i}'}}{\sqrt {\mathrm {P} (x_{i}')}}$

est minimum pour $\varepsilon _{i}=0\,;$ ou, en d’autres termes, si la dérivée seconde, par rapport à $t,$ du radical

${\sqrt {\mathrm {P} \left({\frac {dx_{i}}{dx_{1}}}+\varepsilon _{i}t\right)}}$

est positive.

Mais, quels que soient les ${\frac {dx_{i}}{dx_{1}}}$ et les $\varepsilon _{i},$ on aura

$\mathrm {P} \left({\frac {dx_{i}}{dx_{1}}}+\varepsilon _{i}t\right)=at^{2}+2bt+c,$

$a,\,b,\,c$ étant indépendants de $t\,;$ la dérivée seconde du radical est alors égale à

${\frac {ac-b^{2}}{\left(at^{2}+2bt+c\right)^{\frac {3}{2}}}}\cdot$

Comme le polynôme $\mathrm {P}$ est essentiellement positif, cette expression est aussi toujours positive et la condition (A) est toujours remplie.

344.Passons au principe de Maupertuis dans le mouvement relatif. Nous avons alors à envisager l’intégrale

$\int \left[ds\,{\sqrt {\mathrm {H} _{0}+h}}+\omega '(\xi \,d\eta -\eta \,d\xi )\right],$

ou, en prenant $\xi$ pour variable indépendante,

$\int d\xi \,\left[{\sqrt {(\mathrm {H} _{0}+h)(1+\eta '^{2})}}+\omega '(\xi \eta '-\eta )\right].$

Il faut donc rechercher si la dérivée seconde par rapport à $\eta '$ de

${\sqrt {(\mathrm {H} _{0}+h)(1+\eta '^{2})}}+\omega '(\xi \eta '-\eta )$

est positive ; or, cette dérivée est

${\frac {\sqrt {\mathrm {H} _{0}+h}}{\left(1+\eta '^{2}\right)^{\frac {3}{2}}}}\cdot$

La condition (A) est donc toujours remplie.

Ainsi la condition (A) est remplie d’elle-même dans tous les cas que nous aurons à examiner.

Foyers maupertuisiens.

345.Les foyers cinétiques ne sont pas tout à fait les mêmes suivant qu’on envisage l’action hamiltonienne ou l’action maupertuisienne. Pour mieux nous en rendre compte, supposons deux degrés de liberté seulement et soient $x$ et $y$ les deux variables qui définissent la position du système et que nous pourrons regarder comme les coordonnées d’un point dans un plan.

Soient

${\begin{aligned}x&=f_{1}(t),&y&=f_{2}(t)\end{aligned}}$

les équations d’une trajectoire $(\mathrm {T} )$ qui sera une courbe plane. Posons

${\begin{aligned}x&=f_{1}(t)+\xi ,&y&=f_{2}(t)+\eta ,\end{aligned}}$

et, négligeant les carrés de $\xi$ et de $\eta ,$ formons les équations aux variations. Comme elles sont linéaires et du quatrième ordre, on aura donc

${\begin{aligned}\xi &=a_{1}\xi _{1}+a_{2}\xi _{2}+a_{3}\xi _{3}+a_{4}\xi _{4},\\\eta &=a_{1}\eta _{1}+a_{2}\eta _{2}+a_{3}\eta _{3}+a_{4}\eta _{4},\end{aligned}}$

les $a_{i}$ étant des constantes d’intégration, les $\xi _{i}$ et les $\eta _{i}$ des fonctions de $t.$

L’équation du n^o 341,

$\Delta (t',t'')=0,$

s’écrit alors

(1)

$\left|{\begin{array}{cccc}\xi _{1}'&\xi _{2}'&\xi _{3}'&\xi _{4}'\\\eta _{1}'&\eta _{2}'&\eta _{3}'&\eta _{4}'\\\xi _{1}''&\xi _{2}''&\xi _{3}''&\xi _{4}''\\\eta _{1}''&\eta _{2}''&\eta _{3}''&\eta _{4}''\end{array}}\right|=0.$

C’est cette équation qui définit les foyers hamiltoniens.

Elle exprime que le point $x,\,y$ qui décrit la trajectoire $(\mathrm {T} )$ et le point $x+\xi ,$ $y+\eta$ qui décrit la trajectoire infiniment voisine $(\mathrm {T} ')$ se trouvent à deux époques différentes, à savoir aux époques $t'$ et $t'',$ séparés par une distance infiniment petite d’ordre supérieur.

Mais ce ne sont pas là les conditions que doivent remplir les foyers maupertuisiens. Deux des points de la trajectoire $(\mathrm {T} ),$ à savoir les deux points $\mathrm {M} '$ et $\mathrm {M} ''$ qui correspondent aux époques $t'$ et $t'',$ doivent être à une distance infiniment petite d’ordre supérieur de la trajectoire $(\mathrm {T} ').$ Mais il n’est pas nécessaire que le point mobile qui parcourt $(\mathrm {T} ')$ passe précisément à l’époque $t'',$ par exemple, infiniment près de $\mathrm {M} ''.$ En revanche, la constante des forces vives doit avoir la même valeur pour $(\mathrm {T} )$ et pour $(\mathrm {T} ')\,;$ cette dernière condition n’est pas imposée aux foyers hamiltoniens.

L’une des solutions des équations aux variations est

${\begin{aligned}\xi &=f_{1}'(t),&\eta &=f_{2}'(t),\end{aligned}}$

Nous pouvons donc supposer

${\begin{aligned}\xi _{1}'&=f_{1}'(t'),&\eta _{1}'&=f_{2}'(t'),&\xi _{1}''&=f_{1}'(t''),&\eta _{1}''&=f_{2}'(t'').\end{aligned}}$

Ainsi sont définies les deux fonctions $\xi _{1}$ et $\eta _{1}.$

D’autre part, la différence entre la constante des forces vives relative à $(\mathrm {T} )$ et la constante des forces vives relative à $(\mathrm {T} ')$ est infiniment petite ; c’est évidemment une fonction linéaire des quatre constantes infiniment petites $a_{1},\,a_{2},\,a_{3},\,a_{4}.$

Nous pouvons, sans restreindre la généralité, supposer que cette différence est précisément égale à $a_{4}$.

Alors, la condition pour que la valeur de la constante des forces vives soit la même pour $(\mathrm {T} )$ et $(\mathrm {T} '),$ c’est que $a_{4}=0,$ ou bien

${\begin{alignedat}{4}\xi &=a_{1}\xi _{1}&{}+{}&a_{2}\xi _{2}&{}+{}&a_{3}\xi _{3},\\\eta &=a_{1}\eta _{1}&{}+{}&a_{2}\eta _{2}&{}+{}&a_{3}\eta _{3}.\end{alignedat}}$

Maintenant, pour $t=t',$ $\xi$ et $\eta$ doivent être nuls, d’où les équations

${\begin{alignedat}{4}a_{1}\xi _{1}'&{}+{}&a_{2}\xi _{2}'&{}+{}&a_{3}\xi _{3}'&=0,\\a_{1}\eta _{1}'&{}+{}&a_{2}\eta _{2}'&{}+{}&a_{3}\eta _{3}'&=0.\end{alignedat}}$

D’autre part,la valeur de $x+\xi ,$ $y+\eta$ pour $t=t''\!+\varepsilon$ doit être la même (à des infiniment petits près d’ordre supérieur) que celle de $x$ et de $y$ pour $t=t'',$ ce qui s’écrit

${\begin{alignedat}{4}(\varepsilon +a_{1})&&\,\xi _{1}''&{}+{}&a_{2}\xi _{2}''&{}+{}&a_{3}\xi _{3}''&=0,\\(\varepsilon +a_{1})&&\,\eta _{1}''&{}+{}&a_{2}\eta _{2}''&{}+{}&a_{3}\eta _{3}''&=0,\end{alignedat}}$

d’où, par élimination,

(2)

$\left|{\begin{array}{cccc}\xi _{2}'&\xi _{3}'&\xi _{1}'&0\\\eta _{2}'&\eta _{3}'&\eta _{1}'&0\\\xi _{2}''&\xi _{3}''&0&\xi _{1}''\\\eta _{2}''&\eta _{3}''&0&\eta _{1}''\end{array}}\right|=0.$

En développant le déterminant, on trouve

$\left|{\begin{array}{cc}\xi _{1}'\eta _{2}'-\xi _{2}'\eta _{1}'&\xi _{1}'\eta _{3}'-\xi _{3}'\eta _{1}'\\\xi _{1}''\eta _{2}''-\xi _{2}''\eta _{1}''&\xi _{1}''\eta _{3}''-\xi _{3}''\eta _{1}''\end{array}}\right|=0$

et, en posant

${\frac {\xi _{1}\eta _{2}-\xi _{2}\eta _{1}}{\xi _{1}\eta _{3}-\xi _{3}\eta _{1}}}=\zeta (t),$

l’équation (2) devient

(3)

$\zeta (t')=\zeta (t'').$

Application aux solutions périodiques.

346.Si nous avons affaire à une solution périodique de période $2\pi ,$ les fonctions $f_{1}(t)$ et $f_{2}(t)$ du numéro précédent seront périodiques de période $2\pi \,;$ il en est de même de

${\begin{aligned}\xi _{1}&=f_{1}'(t),&\eta _{1}&=f_{2}'(t).\end{aligned}}$

De plus, les équations aux variations admettront, d’après le Chapitre IV, d’autres solutions particulières qui seront de la forme

${\begin{aligned}\xi &=e^{\alpha t}\varphi _{2}(t),&\eta &=e^{\alpha t}\psi _{2}(t)\,;\\\xi &=e^{-\alpha t}\varphi _{3}(t),&\eta &=e^{-\alpha t}\psi _{3}(t)\,;\\\xi &=\varphi _{4}(t)+\beta tf_{1}'(t),&\eta &=\psi _{4}(t)+\beta tf_{2}'(t).\end{aligned}}$

Dans ces équations, $\beta$ est une constante, $\alpha$ et $-\alpha$ sont les exposants caractéristiques, les $\varphi$ et les $\psi$ sont des fonctions périodiques.

Soit

$\mathrm {F} \left(x,y,{\frac {dx}{dt}},{\frac {dy}{dt}}\right)=\mathrm {const.}$

l’équation des forces vives ; on devra avoir

${\frac {d\mathrm {F} }{dx}}\,\xi +{\frac {d\mathrm {F} }{dy}}\,\eta +{\frac {d\mathrm {F} }{d{\dfrac {dx}{dt}}}}{\frac {d\xi }{dt}}+{\frac {d\mathrm {F} }{d{\dfrac {dy}{dt}}}}{\frac {d\eta }{dt}}=\mathrm {A} ,$

$\mathrm {A}$ étant une constante. Si, dans cette équation, nous remplaçons $\xi$ et $\eta$ par $e^{\alpha t}\varphi _{2},$ $e^{\alpha t}\psi _{2},$ le premier membre devient une fonction périodique de $t$ multipliée par et $e^{\alpha t}$ et, comme il doit être constant, il faut qu’il soit nul.

On aura donc

$\mathrm {A} =0$.

Cela veut dire que les deux trajectoires infiniment voisines qui ont pour équations

${\begin{aligned}x&=f_{1}(t),&y&=f_{2}(t)\end{aligned}}$

et

${\begin{aligned}x&=f_{1}(t)+e^{\alpha t}\varphi _{2}(t),&y&=f_{2}(t)+e^{\alpha t}\psi _{2}(t),\end{aligned}}$

correspondent à une même valeur de la constante des forces vives.

On verrait de même qu’il en est encore ainsi de la trajectoire qui a pour équation

${\begin{aligned}x&=f_{1}(t)+e^{-\alpha t}\varphi _{2}(t),&y&=f_{2}(t)+e^{-\alpha t}\psi _{2}(t),\end{aligned}}$

Rien n’empêche donc de poser

${\begin{aligned}\xi _{2}&=e^{\alpha t}\varphi _{2},&\eta _{2}&=e^{\alpha t}\psi _{2},\\\xi _{3}&=e^{-\alpha t}\varphi _{3},&\eta _{3}&=e^{-\alpha t}\psi _{3}.\end{aligned}}$

Alors $\zeta (t)$ est de la forme suivante

$\zeta (t)=e^{2\alpha r}\mathrm {G} (t),$

$\mathrm {G} (t)$ étant une fonction périodique.

Cas des solutions stables.

347.Nous devons maintenant distinguer deux cas :

1^o La solution est stable et $\alpha ^{2}$ est négatif. Dans ce cas $\xi _{2}$ et $\xi _{3},$ $\eta _{2}$ et $\eta _{3}$ sont imaginaires conjugués ; $\zeta$ et $\mathrm {G}$ ont pour module l’unité. Nous allons faire trois hypothèses que nous justifierons plus loin.

1^o Supposons d’abord que $\mathrm {G} (t)$ ne devienne jamais ni nul ni infini ;

2^o Que la fonction

$t+{\frac {1}{2\alpha }}\log \mathrm {G} (t)=\tau$

qui est essentiellement réelle soit aussi constamment croissante ;

3^o Supposons de plus que $\log \mathrm {G} (t)$ soit une fonction périodique.

Alors, l’équation (3) pourra s’écrire, en appelant $\tau '$ et $\tau ''$ les deux valeurs de $\tau$ qui correspondent à $t'$ et à $t'',$

$\tau ''-\tau '={\frac {k\,i\,\pi }{\alpha }}$  ($k$ étant entier).

À chaque valeur de $t$ correspond une seule valeur de $\tau$ et à chaque valeur de $\tau$ une seule valeur de $t\,;$ nous ne pouvons donc avoir $k=0$ sans avoir $t'=t''\,;$ et si nous voulons $t''>t',$ il faut que $k$ soit positif.

En faisant $k=1$ on donnera à $t''-t'$ la plus petite valeur ; il vient

$\tau ''-\tau '={\frac {i\,\pi }{\alpha }}$

et le point $\mathrm {M} ''$ est alors le foyer de $\mathrm {M} '.$

Mais il importe de remarquer une chose.

Pour que le raisonnement qui précède s’applique, il faut que $\log \mathrm {G} (t)$ soit une fonction périodique ; mais, en général, tout ce que nous savons, c’est que $\mathrm {G} (t)$ est une fonction périodique, et il en résulte simplement que

$\log \mathrm {G} (t)$

augmente d’un multiple de $2i\pi ,$ par exemple de $2ki\pi$ quand $t$ augmente de $2\pi .$ Alors

$\log \mathrm {G} (t)-ikt,$

est une fonction périodique.

Posons alors

${\begin{aligned}\mathrm {G} '(t)&=\mathrm {G} (t)\,e^{-ikt},\\\alpha '&=\alpha +{\frac {ik}{2}}\,;\end{aligned}}$

il viendra

$\zeta (t)=e^{2\alpha t}\mathrm {G} (t)=e^{2\alpha 't}\mathrm {G} '(t).$

On posera alors, non plus

$\tau =t+{\frac {1}{2\alpha }}\log \mathrm {G} (t),$

mais

$\tau =t+{\frac {1}{2\alpha '}}\log \mathrm {G} '(t)\,;$

comme $\log \mathrm {G} (t)$ sera périodique, les conclusions qui précèdent subsistent, l’équation (3) s’écrira

$\tau ''-\tau '={\frac {m\,i\,\pi }{\alpha '}}$  ($m$ étant entier)

et, de plus, $\mathrm {M} ''$ sera le foyer de $\mathrm {M} '$ si

$\tau ''-\tau '={\frac {i\,\pi }{\alpha '}}\cdot$

348..Ainsi se trouve justifiée l’une de nos trois hypothèses, que $\log \mathrm {G} (t)$ doit être périodique. Je dis maintenant que la fonction $\tau$ doit, comme nous l’avons supposé, être constamment croissante.

Supposons en effet que cette fonction admette un maximum $\tau _{0}$ pour $t=t_{0}\,;$ nous pourrions alors trouver deux époques $t_{1}'$ et $t_{1}''$ telles que les valeurs correspondantes $\tau _{1}'$ et $\tau _{1}''$ de la fonction $\tau$ soient égales, et deux autres époques, $t_{2}'$ et $t_{2}''$ telles que $\tau _{2}'=\tau _{2}''\,;$ telles enfin que les cinq époques d’ailleurs très voisines l’une de l’autre, satisfassent aux inégalités

$t_{2}'<t_{1}'<t_{0}<t_{1}''<t_{2}''.$

Alors $t_{1}''$ serait le foyer de $t_{1}',$ $t_{2}''$ celui de $t_{2}'\,;$ or, nous avons vu plus haut que de pareilles inégalités sont impossibles quand la condition (A) est remplie.

Je dis maintenant que $\mathrm {G} (t)$ ne peut s’annuler ; en effet, on a

$\zeta (t)={\frac {\xi _{1}\eta _{2}-\xi _{2}\eta _{1}}{\xi _{1}\eta _{3}-\xi _{3}\eta _{1}}}\cdot$

Le numérateur et le dénominateur de $\zeta (t)$ sont imaginaires conjugués ; si l’un d’eux s’annule, l’autre s’annule également, de sorte que la fonction $\zeta (t)$ ne peut devenir ni nulle ni infinie.

Ainsi se trouvent justifiées toutes nos hypothèses.

Solutions instables.

349.Supposons maintenant la solution instable et $\alpha ^{2}$ positif ; dans ce cas $\xi _{2},\,\eta _{2},$ $\xi _{3},\,\eta _{3},$ $\zeta ,\,\alpha ,$ $\mathrm {G}$ sont réels.

Pour la même raison que plus haut, la fonction $\tau$ sera constamment croissante ; mais deux hypothèses sont possibles :

1^o Ou bien $\zeta (t)$ ne peut s’annuler ni devenir infini et croît constamment de $0$ à $+\infty$ quand $t$ croît de $-\infty$ à $+\infty .$

Il arrive alors qu’aucun point de notre solution périodique n’a de foyer maupertuisien.

2^o Ou bien $\zeta (t)$ peut s’annuler pour $t=t_{0}\,;$ il s’annulera alors aussi pour $t=t_{0}+2\pi ,$ et comme il ne peut avoir ni maximum, ni minimum, il faut qu’il devienne infini dans l’intervalle. De même, si $\zeta (t)$ peut devenir infini, il faut aussi qu’il puisse s’annuler.

Supposons donc, pour fixer les idées, que $\zeta (t)$ devienne infini pour

$t=t_{0},\quad t_{1},\quad t_{0}+2\pi$

et pour les valeurs qui en diffèrent d’un multiple de $2\pi$ et s’annule pour

$t=t_{0}',\quad t_{1}',\quad t_{0}'+2\pi .$

Je suppose d’ailleurs

$t_{0}<t_{0}'<t_{0}<t_{1}'<t_{0}+2\pi .$

D’ailleurs, quand $t$ croît de $t_{0}$ à $t_{1},$ ou de $t_{1}$ à $t_{2},$ ou de $t_{2}$ à $t_{0}+2\pi ,$ $\zeta (t)$ croît constamment de $-\infty$ à $+\infty .$

La trajectoire fermée $(\mathrm {T} )$ qui représente notre solution périodique sera donc partagée en deux arcs dont les extrémités correspondront aux valeurs de $t$

$t_{0},\quad t_{1},\quad t_{0}+2\pi .$

Chacun des points de l’un des arcs aura son premier foyer sur l’arc suivant.

J’ajoute que les points qui correspondent aux valeurs de $t$

$t_{0},\quad t_{1},\quad t_{0}',\quad t_{1}'$

coïncident avec leurs deuxièmes foyers.

Soient $t''$ une valeur de $t$ correspondant à un point quelconque de $(\mathrm {T} )$ et $t_{n}''$ la valeur de $t$ qui correspond à son $n$^ième foyer, on aura

$\lim {\frac {t_{n}''-t''}{n}}={\frac {2\pi }{2}}\cdot$

Mais ce n’est pas tout ; on aura

$e^{2\alpha t_{n}''}\mathrm {G} (t_{n}'')=e^{2\alpha t''}\mathrm {G} (t'').$

Si $n$ est très grand et si $\mathrm {G} (t'')$ n’est pas infini, comme $t_{n}''-t''$ est très grand et que nous supposons $\alpha$ positif, $\mathrm {G} (t_{n}'')$ sera très petit, de sorte que si $t''$ est, par exemple, compris entre $t_{0}$ et $t_{1},$ la différence

$t_{2n}''-2n\pi$

tendra vers $t_{0}'$ quand $n$ croîtra indéfiniment.

Si $n$ tend vers $-\infty ,$ cette différence tendra vers $t_{0}$ ou vers $t_{1}$ selon que $t''$ sera compris entre $t_{0}$ et $t_{0}'$ ou entre $t_{0}'$ et $t_{1}.$ J’ajouterai que la différence $t_{2n}''-2n\pi$ est, ou constamment croissante, ou constamment décroissante avec $n.$

Les valeurs $t_{0}',\,t_{1}'$ correspondent aux points où

$\xi _{1}\eta _{2}-\xi _{2}\eta _{1}=0\,;$

mais $\xi _{1}\eta _{2}-\xi _{2}\eta _{1}$ est une fonction périodique multipliée par $e^{\alpha t}\,;$ or, une fonction périodique doit dans une période s’annuler un nombre pair de fois.

Par conséquent, la trajectoire fermée $(\mathrm {T} )$ sera partagée par les points $t_{0},$ $t_{1},$ $t_{0}+2\pi$ en un certain nombre d’arcs et ce nombre sera toujours pair.

350.Au point de vue qui nous occupe, les solutions périodiques instables peuvent donc se répartir en deux catégories. Mais on pourrait se demander si ces deux catégories existent réellement. Il convient donc d’en citer des exemples.

Soient $\rho$ et $\omega$ les coordonnées polaires d’un point mobile dans un plan ; les équations du mouvement s’écriront

(1)

${\begin{aligned}{\frac {d^{2}\rho }{dt^{2}}}&=\left({\frac {d\omega }{dt}}\right)^{2}\rho +{\frac {d\mathrm {U} }{d\rho }},&\rho ^{2}{\frac {d^{2}\omega }{dt^{2}}}+2\rho {\frac {d\rho }{dt}}{\frac {d\omega }{dt}}&={\frac {d\mathrm {U} }{d\omega }}\cdot \end{aligned}}$

Supposons que, pour $\rho =1,$ on ait

${\begin{aligned}\mathrm {U} &=0,&{\frac {d\mathrm {U} }{d\omega }}&=0,&{\frac {d\mathrm {U} }{d\rho }}&=-1,&{\frac {d^{2}\mathrm {U} }{d\rho ^{2}}}&=\varphi (\omega )\,;\end{aligned}}$

les équations (1) admettront pour solutions

$\rho =1,\quad \omega =t$

et cette solution correspondra à une trajectoire fermée qui sera une circonférence.

Posons

${\begin{aligned}\rho &=1+\zeta ,&\omega &=t+\nu \end{aligned}}$

et formons les équations aux variations ; elles s’écriront

${\begin{aligned}{\frac {d^{2}\zeta }{dt^{2}}}&=\zeta +2{\frac {d\nu }{dt}}+\zeta \varphi (t),&{\frac {d^{2}\nu }{dt^{2}}}+2{\frac {d\zeta }{dt}}&=0.\end{aligned}}$

La seconde s’intègre immédiatement

${\frac {d\zeta }{d\beta }}+2\zeta =\mathrm {const.} \,;$

mais cette constante doit être nulle si nous voulons que la constante des forces vives ait même valeur pour la trajectoire $(\mathrm {T} )$ et pour la trajectoire infiniment voisine.

Si donc on remplace ${\frac {d\nu }{dt}}$ par $-2\zeta ,$ la première équation aux variations deviendra

(2)

${\frac {d^{2}\zeta }{dt^{2}}}=\zeta \left[\varphi (t)-3\right].$

L’équation (2) qu’il nous reste à intégrer est une équation linéaire à coefficient périodique.

Ces équations ont été traitées dans les n^os 29 et 189 (voir en outre Chapitre IV, passim).

On sait qu’elles admettent deux solutions de la forme suivante :

${\begin{aligned}\zeta &=e^{\alpha t}\mathrm {G} (t),&\zeta &=e^{-\alpha t}\mathrm {G} _{1}(t),&\end{aligned}}$

$\mathrm {G}$ et $\mathrm {G} _{1}$ étant des fonctions périodiques.

Nous allons trouver des exemples de tous les cas distingués plus haut. Supposons d’abord que $\varphi$ se réduise à une constante $\mathrm {A}$ (cas des forces centrales).

Si $\mathrm {A} <3,$ on aura une solution périodique stable.

Si $\mathrm {A} >3,$ il n’y aura pas sur $(\mathrm {T} )$ de foyer maupertuisien et nous aurons une solution périodique instable de la première catégorie.

Il me reste à faire voir qu’il peut aussi y avoir des solutions périodiques instables de la deuxième catégorie.

La solution sera instable et de la deuxième catégorie si $\mathrm {G}$ s’annule de telle façon que le rapport

$e^{2\alpha t}{\frac {\mathrm {G} }{\mathrm {G} _{1}}},$

qui correspond à la fonction $\zeta (t)$ des numéros précédents puisse s’annuler et par conséquent devenir infini.

Or, on peut évidemment construire une fonction périodique $\mathrm {G}$ satisfaisant aux conditions suivantes :

1^o Elle admettra deux zéros simples et deux seulement ;

2^o Ces zéros annuleront également

${\frac {d^{2}\mathrm {G} }{dt^{2}}}+2\alpha {\frac {d\mathrm {G} }{dt}}\cdot$

Il en résulte que toutes les fois que

$\zeta =e^{\alpha t}\mathrm {G}$

s’annulera, sa dérivée seconde s’annulera également de telle façon que le rapport

${\frac {1}{\zeta }}{\frac {d^{2}\zeta }{dt^{2}}}=\varphi -3$

restera fini.

On peut évidemment construire une fonction $\mathrm {G}$ qui satisfasse à ces conditions ; la fonction périodique construite à l’aide de cette fonction $\mathrm {G}$ correspondra à une solution périodique instable de la deuxième catégorie.

Comme exemple de fonction $\mathrm {G}$ satisfaisant à cette condition, nous pouvons prendre

$\mathrm {G} =\sin t-{\frac {\alpha }{4}}\left(\cos t-\cos 3t\right).$

Cette fonction s’annule pour $t=0$ et $t=\pi \,;$ et elle n’a pas d’autre zéro si

$\alpha <{\frac {1}{\sqrt {5}}}\cdot$

D’ailleurs, pour $t=0$ et pour $t=\pi ,$ on a

${\frac {d^{2}\mathrm {G} }{dt^{2}}}+2\alpha {\frac {d\mathrm {G} }{dt}}=0.$

Pour que le rapport ${\frac {\mathrm {G} }{\mathrm {G} _{1}}}$ s’annule, il ne suffit pas que $\mathrm {G}$ s’annule, il faut encore que $\mathrm {G} _{1}$ ne s’annule pas.

Or, c’est ce qui arrive, car si $\mathrm {G}$ et $\mathrm {G} _{1}$ s’annulaient à la fois, les deux solutions

${\begin{aligned}\zeta &=e^{\alpha t}\mathrm {G} (t),&\zeta &=e^{-\alpha t}\mathrm {G} _{1}(t)\end{aligned}}$

ne pourraient différer que par un facteur constant (puisqu’elles satisfont à une même équation différentielle du second ordre) et cela est absurde.

351. Un point sur lequel je veux attirer l’attention, c’est que les solutions instables de la première et de la deuxième catégorie forment deux ensembles séparés de telle façon qu’on ne peut passer de l’une à l’autre d’une manière continue sans passer par l’intermédiaire des solutions stables.

Bornons-nous d’abord au cas particulier du numéro précédent et reprenons l’équation

(2)

${\frac {d^{2}\zeta }{dt^{2}}}=\zeta \left(\varphi -3\right).$

Faisons varier la fonction $\varphi$ d’une manière continue et voyons si l’on pourra passer immédiatement d’une solution instable de la première catégorie à une solution instable de la deuxième catégorie. Pour cela, il faut que la fonction $\mathrm {G}$ qui est réelle soit d’abord incapable de s’annuler et ensuite susceptible de s’annuler. On passerait donc du cas où l’équation $\mathrm {G} =0$ a toutes ses racines imaginaires au cas où elle a des racines réelles. Au moment du passage, elle aurait une racine double ou plus généralement multiple d’ordre $2m.$

Ce zéro, qui serait d’ordre $2m$ pour $\mathrm {G} ,$ serait d’ordre $2m-1$ pour ${\frac {d\mathrm {G} }{dt}},$ d’ordre $2m-2$ pour ${\frac {d^{2}\mathrm {G} }{dt^{2}}},$ de sorte que l’expression

${\frac {{\dfrac {d^{2}\mathrm {G} }{dt^{2}}}+2\alpha \,{\dfrac {d\mathrm {G} }{dt}}+\alpha ^{2}\mathrm {G} }{\mathrm {G} }}$

deviendrait infinie, ce qui est impossible, puisqu’elle est égale à $\varphi -3.$

Au contraire, on peut passer d’une solution stable à une solution instable de l’une ou de l’autre catégorie.

Pour une solution stable, en effet, $\mathrm {G}$ est imaginaire. Au moment où la solution deviendra instable, la partie imaginaire de $\mathrm {G}$ deviendra identiquement nulle ; si, à ce moment, la partie réelle de $\mathrm {G}$ a des zéros, on passera à une solution instable de la deuxième catégorie ; si cette partie réelle ne s’annule jamais, on passera à une solution instable de la première catégorie.

Il n’y a d’ailleurs aucune difficulté à passer du cas où l’équation

partie réelle de $\mathrm {G} =0$

a toutes ses racines imaginaires à celui où cette équation a des racines réelles, pourvu qu’au moment du passage la partie imaginaire de $\mathrm {G}$ ne soit pas nulle.

352.Pour mieux faire comprendre ce qui précède, je vais revenir à un exemple qui nous est déjà familier.

Revenons à l’équation de Gyldén, c’est-à-dire à l’équation (1) du n^o 178 (t. II). Nous donnerons à cette équation le numéro (3) et nous l’écrirons

(3)

${\frac {d^{2}x}{dt^{2}}}=x\left(-q^{2}+q_{1}\cos 2t\right).$

On voit qu’elle est de même forme que l’équation (2). Nous avons vu que cette équation a, comme l’équation (2), deux intégrales de la forme

$e^{\alpha t}\mathrm {G} ,\quad e^{-\alpha t}\mathrm {G} _{1},$

que nous avons écrites dans la notation du n^o 178, sous la forme

$e^{iht}\varphi _{1},\quad e^{-iht}\varphi _{2}.$

Le cas de $h$ réel correspond alors au cas des solutions stables et le cas de $h$ imaginaire à celui des solutions instables.

Nous avons envisagé aussi deux intégrales remarquables ; la première paire

$\mathrm {F} (t)$

$\left[\mathrm {F} (0)=1,\quad \mathrm {F} '(0)=0\right];$

la seconde impaire

$f(t)$

$\left[f(0)=0,\quad f'(0)=1\right];$

et nous avons trouvé les conditions

${\begin{array}{c}\mathrm {F} (\pi )f'(\pi )-f(\pi )\mathrm {F} '(\pi )=1,\\[0.75ex]\mathrm {F} (\pi )=f'(\pi )=\cos h\pi .\end{array}}$

Je renvoie maintenant à la figure de la page 243 (Tome II) où, regardant $q$ et $q_{1}$ comme les coordonnées rectangulaires d’un point, nous avons séparé les régions correspondant aux solutions stables de celles qui correspondent aux solutions instables. Ces dernières sont représentées couvertes de hachures.

Ces diverses régions sont séparées les unes des autres par quatre courbes analytiques dont j’ai donné les équations page 241 (Tome II).

Voici ces équations

(α) 	$\mathrm {F} (\pi )=\quad 1,$	$\mathrm {F} '(\pi )=0,$
(β)	$\mathrm {F} (\pi )=\quad 1,$	$f\,(\pi )=0,$
(γ)	$\mathrm {F} (\pi )=\;-1,$	$\mathrm {F} '(\pi )=0,$
(δ)	$\mathrm {F} (\pi )=\;-1,$	$f\,(\pi )=0.$

À quelle catégorie appartiennent les solutions instables qui correspondent à nos régions couvertes de hachures ? Il est clair d’abord que les solutions instables qui correspondent à l’une de ces régions sont toute de la même catégorie. Cela résulte immédiatement de ce qui précède.

Or, en un point de l’une des courbes (β) et (δ), la fonction $\mathrm {G}$ se réduit à $f(t)$ et cette fonction peut s’annuler puisqu’elle est impaire. Donc, si une région est limitée par un arc de l’une des courbes (β) et (δ), les solutions correspondantes seront de la seconde catégorie.

Mais il en est ainsi de toutes nos régions. Donc toutes nos solutions instables sont de la seconde catégorie.

Il est aisé de transformer notre exemple de telle façon que l’on ait des solutions des deux catégories. Il suffit de remplacer $q^{2}$ par $q$ de façon que ce coefficient puisse devenir négatif.

Notre équation (3) s’écrit alors

(3 bis)

${\frac {d^{2}x}{dt^{2}}}=x\left(-q+q_{1}\cos 2t\right).$

Prenons toujours $q$ et $q_{1}$ pour coordonnées rectangulaires et construisons une figure analogue à celle de la page 241. La partie de la figure située à droite de l’axe des $q_{1}$ du côté des $q$ positifs sera analogue à la figure de la page 241. Mais nous aurons à gauche de l’axe des $q_{1},$ du côté des $q$ négatifs, une région couverte de hachures, limitée par une espèce de parabole tangente à l’axe des $q_{1}.$

Les régions hachées de droite correspondront, nous venons de le voir, à des solutions de la seconde catégorie ; mais il n’en sera pas de même de la région hachée de gauche.

Il suffit pour s’en convaincre de faire $q_{1}=0,$ d’où

$x=e^{t{\sqrt {-q}}}\,;\qquad \alpha ={\sqrt {-q}}\,;\qquad \mathrm {G} =1.$

353.Je n’ai encore fait la discussion que dans un cas particulier. Pour l’étendre au cas général, je vais montrer qu’on est toujours amené à une équation de même forme que l’équation (2) du numéro précédent.

Considérons d’abord le cas du mouvement absolu ; si $\mathrm {U}$ est la fonction des forces et si $x$ et $y$ sont les coordonnées cartésiennes d’un point dans un plan, les équations du mouvement s’écriront

(1)

${\begin{aligned}x''&={\frac {d\mathrm {U} }{dx}},&y''&={\frac {d\mathrm {U} }{dy}},\end{aligned}}$

et les équations aux variations

(2)

$\left\{{\begin{alignedat}{3}\xi ''&={\frac {d^{2}\mathrm {U} }{dx^{2}}}\,\xi &{}+{}&{\frac {d^{2}\mathrm {U} }{dx\,dy}}\,\eta ,\\\eta ''&={\frac {d^{2}\mathrm {U} }{dx\,dy}}\,\xi &{}+{}&{\frac {d^{2}\mathrm {U} }{dy^{2}}}\,\eta .\end{alignedat}}\right.$

Je représente pour plus de brièveté par des accents les dérivations par rapport à $t.$ Ainsi $\xi ''$ représente ici ${\frac {d^{2}\xi }{dt^{2}}}$ et non plus, comme dans le n^o 341, la valeur de $\xi$ pour $t=t''.$

L’intégrale des forces vives s’écrira

${\frac {x'^{2}+y'^{2}}{2}}=\mathrm {U} +h,$

et l’intégrale correspondante de (2)

$x'\xi '+y'\eta '={\frac {d\mathrm {U} }{dx}}\,\xi +{\frac {d\mathrm {U} }{dy}}\,\eta +\delta h$  ($\delta h$ étant une constante).

Pour l’application du principe de Maupertuis, il faut supposer

$\delta h=0,$

de sorte que nous aurons

$x'\xi '+y'\eta '={\frac {d\mathrm {U} }{dx}}\,\xi +{\frac {d\mathrm {U} }{dy}}\,\eta ,$

ou bien

(3)

$x'\xi '+y'\eta '=x''\xi +y''\eta .$

Nos équations (2) et (3) admettront alors trois solutions linéairement indépendantes que nous avons appelées au n^o 345

(4)

$\left\{{\begin{aligned}\xi _{1}&=x',&\eta _{1}&=y'.\\\xi _{2}&&\eta _{2}&\\\xi _{3}&&\eta _{3}&\end{aligned}}\right.$

Posons

(5)

$\theta =\xi y'-\eta x'$

Si alors nous appelons $\theta _{1},\,\theta _{2},\,\theta _{3}$ les trois valeurs de $\theta$ qui correspondent aux trois solutions (4), nous aurons $\theta _{1}=0$ et la fonction que nous avons appelée $\zeta (t)$ au n^o 343 ne sera autre chose que

$\zeta (t)={\frac {\theta _{2}}{\theta _{3}}}\cdot$

De l’équation (5) on tire

(6)

$\theta '=\xi 'y'-\eta 'x'+\xi y''-\eta x''$

et

$\theta ''=\xi y'''-\eta y'''+\xi ''y'-\eta ''x'+2(\xi 'y''-\eta 'x'').$

Mais $x'$ et $y'$ satisfont aux équations (2), de sorte que l’on a

${\begin{alignedat}{4}x''&={\frac {d^{2}\mathrm {U} }{dx^{2}}}\,x'&&+{\frac {d^{2}\mathrm {U} }{dx\,dy}}\,y',\\y''&={\frac {d^{2}\mathrm {U} }{dx\,dy}}\,x'&&+{\frac {d^{2}\mathrm {U} }{dy^{2}}}\,y'.\end{alignedat}}$

Remplaçons dans l’expression de $\theta '',$ les dérivées $x'''$ et $y'''$ par les valeurs ainsi trouvées et les dérivées $\xi ''$ et $\eta ''$ par leurs valeurs (2), il viendra

(7)

$\theta ''-\theta \,\Delta \mathrm {U} =2(\xi 'y''-\eta 'x'').$

Je désigne par $\Delta \mathrm {U}$ (ou plus brièvement par $\Delta$) la somme des deux dérivées secondes ${\frac {d^{2}\mathrm {U} }{dx^{2}}}+{\frac {d^{2}\mathrm {U} }{dy^{2}}}\cdot$

Il est aisé de vérifier l’identité suivante

${\begin{aligned}2(&x'^{2}\!+y'^{2})(\xi 'y''\!-\eta 'x'')\\&-2(x'x''\!+y'y'')(\xi y''\!-\eta x''\!+\xi 'y'\!-\eta 'x')+2(x''^{2}\!+y''^{2})(\xi y'\!-\eta x')\\&=2(y''x'\!-y'x'')(\xi 'x'\!+\eta 'y'\!-\xi x''\!-\eta y''),\end{aligned}}$

ou, en tenant compte de (5), (6), (7) et (3),

(8)

$(x'^{2}+y'^{2})(\theta ''-\theta \Delta )-2(x'x''+y'y'')\theta '+2(x''^{2}+y''^{2})\theta =0.$

Telle est l’équation différentielle qui définit la fonction inconnue $\theta$.

Nous poserons

$\theta =\varphi {\sqrt {x'^{2}\!+y'^{2}}}$

et notre équation deviendra

(9)

${\frac {\varphi ''}{\varphi }}=\Delta -{\frac {x'x'''+y'y'''+3x''^{2}+3y''^{2}}{x'^{2}+y'^{2}}},$

équation de même forme que l’équation (2) du numéro précédent. Les conclusions du numéro précédent subsistent donc ; une solution périodique instable est de la seconde ou de la première catégorie selon que la fonction $\varphi$ peut ou non s’annuler. On ne peut passer directement d’une solution instable de la première catégorie une solution instable de la seconde, mais seulement en passant par des solutions stables.

354.Les mêmes résultats subsistent-ils encore dans le cas du mouvement relatif ? Les équations du mouvement deviennent alors

(1 bis)

${\begin{aligned}x''-2\omega y'&={\frac {d\mathrm {U} }{dx}},&y''+2\omega x'&={\frac {d\mathrm {U} }{dy}},\end{aligned}}$

$\omega$ désignant la vitesse de rotation des axes mobiles.

Les équations des variations seront

(2 bis)

$\left\{{\begin{alignedat}{5}\xi ''-2\omega \eta '&={\frac {d^{2}\mathrm {U} }{dx^{2}}}\,\xi &&+{\frac {d^{2}\mathrm {U} }{dx\,dy}}\,\eta ,\\\eta ''+2\omega \xi '&={\frac {d^{2}\mathrm {U} }{dx\,dy}}\,\xi &&+{\frac {d^{2}\mathrm {U} }{dy^{2}}}\,\eta .\end{alignedat}}\right.$

L’équation des forces vives étant encore vraie, il en sera de même de

(3)

$x'\xi '+y'\eta '=x''\xi +y''\eta .$

Posons encore

$\theta =\xi y'-\eta x',$

les équations (5) et (6) subsisteront.

D’autre part, comme $x'$ et $y'$ doivent satisfaire aux équations (2 bis), on aura

${\begin{alignedat}{5}x'''-2\omega y''&={\frac {d^{2}\mathrm {U} }{dx^{2}}}\,x'&&+{\frac {d^{2}\mathrm {U} }{dx\,dy}}\,y',\\y'''+2\omega x''&={\frac {d^{2}\mathrm {U} }{dx\,dy}}\,x'&&+{\frac {d^{2}\mathrm {U} }{dy^{2}}}\,y'.\end{alignedat}}$

En tenant compte de ces équations ainsi que des équations (2 bis), et en tenant compte également de l’équation (3), on peut simplifier l’expression de $\theta ''$ et l’on retrouve l’équation

(7)

$\theta ''-\theta \,\Delta \mathrm {U} =2(\xi 'y''-\eta 'x'').$

Comme l’identité du numéro précédent est toujours vraie, on retrouvera les équations (8) et (9) ; il n’y a donc rien à changer aux conclusions du numéro précédent.

355.Mais une nouvelle question se pose.

La trajectoire $(\mathrm {T} )$ est une courbe fermée ; nous avons jusqu’à présent cherché à déterminer si un arc $\mathrm {AB}$ de cette courbe correspondait à une action plus petite que tout arc infiniment voisin ayant mêmes extrémités.

Mais nous pouvons également nous demander si cette courbe fermée tout entière correspond à une action plus petite que toute courbe fermée infiniment petite.

Supposons d’abord qu’un point $\mathrm {A}$ de la courbe $(\mathrm {T} )$ ait son premier foyer $\mathrm {B}$ sur la courbe $(\mathrm {T} ),$ de telle façon que l’arc $\mathrm {AB}$ soit plus petit que la courbe fermée tout entière.

C’est ce qui arrive pour les solutions instables de la première catégorie, nous avons vu que pour ces solutions la courbe $(\mathrm {T} )$ se divise en un certain nombre pair d’arcs et que tout point d’un de ces arcs a son premier foyer sur l’arc suivant ; de telle façon qu’en partant d’un point quelconque on rencontrera son premier foyer avant d’avoir fait le tour complet de la courbe $(\mathrm {T} ).$

C’est ce qui arrive également pour certaines solutions stables. Dans le cas des solutions stables, nous avons posé (n^o 347)

$t+{\frac {1}{2\alpha }}\log \mathrm {G} (t)=\tau$

et nous avons vu que le $\tau$ d’un point et celui de son premier foyer diffèrent de ${\frac {i\pi }{\alpha }}\cdot$ Si donc ${\frac {\alpha }{i}}$ est plus grand que ${\frac {1}{2}},$ on rencontrera le foyer d’un point avant d’avoir fait le tour complet de $(\mathrm {T} ).$

S’il en est ainsi, l’action ne peut pas être moindre pour la courbe $(\mathrm {T} )$ que pour toute courbe fermée voisine.

Soit, en effet, $\mathrm {ABCDEA}$ la courbe $(\mathrm {T} )$ et supposons que $\mathrm {D}$ soit le foyer de $\mathrm {C} .$ Comme $\mathrm {E}$ est au delà du foyer de $\mathrm {C} ,$ nous pourrons joindre $\mathrm {C}$ à $\mathrm {E}$ par un arc $\mathrm {CME}$ très voisin de $\mathrm {CDE}$ et correspondant à une action moindre.

Si je représente par $(\mathrm {CME} )$ l’action correspondant à l’arc $\mathrm {CME} ,$ on aura

$(\mathrm {CME} )<(\mathrm {CDE} )$

et, par conséquent,

$(\mathrm {ABCMEA} )<(\mathrm {ABCDEA} ).$

Considérons maintenant une solution stable telle que

${\frac {\alpha }{i}}>{\frac {1}{2}}\,;$

je dis que l’action ne sera pas non plus moindre pour $(\mathrm {T} )$ que pour toute courbe fermée infiniment voisine.

Je fais la figure, pour fixer les idées, en supposant ${\frac {\alpha }{i}}$ compris entre ${\frac {1}{4}}$ et ${\frac {1}{6}},$ de telle façon que l’on rencontre le foyer d’un point avant d’avoir fait trois fois et après avoir fait deux fois le tour de $(\mathrm {T} ).$

Soit $\mathrm {ABCDA}$ la courbe $(\mathrm {T} )\,;$ le foyer $\mathrm {F}$ se trouvera entre $\mathrm {AB}$ et on le rencontrera après avoir fait deux fois le tour de $(\mathrm {T} ).$

Comme $\mathrm {B}$ se trouve au delà de ce foyer, nous pouvons joindre $\mathrm {A}$ à $\mathrm {B}$ par un arc $\mathrm {AEHNKHMEB}$ tel que

$(\mathrm {AEHNKHMEB} )<(\mathrm {ABCABCAB} ).$

Comme on ne rencontre pas le foyer de $\mathrm {A}$ en décrivant l’arc $\mathrm {AB}$ Fig. 10.
sans faire le tour de $(\mathrm {T} ),$ on aura d’autre part

$(\mathrm {AE} +\mathrm {EB} )>(\mathrm {AB} ),$

d’où, en retranchant,

$(\mathrm {EHNKHME} )<(\mathrm {ABCABCA} )$

ou

$(\mathrm {EHNIE} )+(\mathrm {HNKH} )<2(\mathrm {ABCA} ).$

On doit donc avoir ou bien

$(\mathrm {EHME} )<(\mathrm {ABCA} )$

ou bien

$(\mathrm {HNKH} )<(\mathrm {ABCA} ).$

Il y a, en tout cas, une courbe fermée peu différente de $(\mathrm {T} )$ et correspondant à une action moindre.

Donc, pour qu’une courbe fermée corresponde à une action moindre que toute courbe fermée infiniment voisine, il faut que cette courbe fermée corresponde à une solution périodique instable de la première catégorie.

356.Cette condition est-elle suffisante ? Pour nous en rendre compte, étudions les solutions asymptotiques correspondant à une pareille solution périodique instable.

Soient

${\begin{aligned}x&=\varphi _{0}(t),&y&=\psi _{0}(t)\end{aligned}}$

les équations de la solution périodique et

${\begin{aligned}x&=\varphi _{0}(t)+\mathrm {A} e^{\alpha t}\varphi _{1}(t)+\mathrm {A} ^{2}e^{2\alpha t}\varphi _{2}(t)+\ldots ,\\y&=\psi _{0}(t)+\mathrm {A} e^{\alpha t}\psi _{1}(t)+\mathrm {A} ^{2}e^{2\alpha t}\psi _{2}(t)+\ldots \end{aligned}}$

celles des solutions asymptotiques. Les fonctions $\varphi _{i}(t)$ et $\psi _{i}(t)$ seront des fonctions périodiques de $t.$ Nous pourrons aussi écrire, en posant $\mathrm {A} e^{\alpha t}=u,$

${\begin{aligned}x&=\varphi _{0}(t)+u\varphi _{1}(t)+\ldots =\Phi (t,u),\\y&=\psi _{0}(t)+u\psi _{1}(t)+\ldots =\Psi (t,u).\end{aligned}}$

Si $u$ est suffisamment petit, $x$ et $y$ seront des fonctions uniformes de $t$ et de $u,$ périodiques par rapport à $t$ de période $2\pi .$

De plus, le déterminant fonctionnel

${\frac {\partial (x,y)}{\partial (t,u)}}={\frac {d\Phi }{dt}}{\frac {d\Psi }{du}}-{\frac {d\Psi }{dt}}{\frac {d\Phi }{du}}$

ne s’annulera pas. En effet, pour $u=0,$ ce déterminant se réduit à

$\varphi _{0}'(t)\psi _{1}(t)-\psi _{0}'\varphi _{1}(t).$

Or cette expression n’est autre chose que l’expression

$\xi _{1}\eta _{2}-\xi _{2}\eta 1$

du n^o 345 divisée par $e^{\alpha t}.$ Elle ne s’annulera donc pas si la solution instable est de la première catégorie.

Donc, le déterminant fonctionnel, ne s’annulant pas pour $u=0,$ ne s’annulera pas non plus pour $u$ suffisamment petit.

Donc, si $u$ est suffisamment petit, $u,$ $\cos t$ et $\sin t$ seront des fonctions uniformes de $x$ et de $y.$

Les équations des solutions asymptotiques s’écrivent

(1)

$\left\{{\begin{aligned}x&=\Phi (t,\mathrm {A} e^{\alpha t})\\y&=\Psi (t,\mathrm {A} e^{\alpha t})\end{aligned}}\right.$

et l’on voit que le déterminant fonctionnel

${\frac {\partial (x,y)}{\partial (t,\mathrm {A} )}}={\frac {\partial (\Phi ,\Psi )}{\partial (t,u)}}\,e^{\alpha t}$

ne peut s’annuler, ce qui veut dire que les courbes (1) ne présentent pas de point double, ne se coupent pas entre elles et ne coupent pas la trajectoire $(\mathrm {T} )$ [tout cela, bien entendu, si l’on suppose $u$ suffisamment petit ; cela ne serait plus vrai si l’on prolongeait Fig. 11.
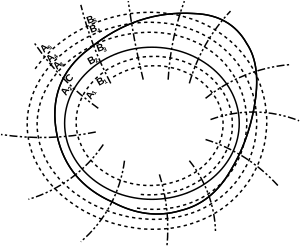indéfiniment les courbes (1) de façon que $u$ devienne très grand].

Les courbes (1) correspondant aux solutions asymptotiques auront donc l’aspect de spirales s’enroulant autour de $(\mathrm {T} ).$ Cet aspect est représenté sur la figure (11). La trajectoire fermée $(\mathrm {T} )$ y est représentée en trait plein, mais je dois avertir qu’il y a sur la figure deux courbes fermées marquées en trait plein ; de ces deux courbes, celle qui est intérieure à l’autre est celle qui représente $(\mathrm {T} ).$

Les courbes spirales (1) sont représentées en trait pointillé − − − −

J’observe qu’il y a deux systèmes de solutions asymptotiques correspondant aux deux exposants caractéristiques égaux et de signe contraire.

Ces solutions asymptotiques du second système seraient des courbes spirales analogues aux courbes (1), mais s’enroulant en sens contraire. Elles ne sont pas représentées sur la figure.

Dans le cas d’une solution instable de la deuxième catégorie, les courbes (1) présenteraient un aspect tout différent ; elles viendraient recouper une infinité de fois la trajectoire fermée $(\mathrm {T} )$ et les points d’intersection formeraient un ensemble infini présentant un nombre fini, d’ailleurs pair, de points limites. Ces points limites correspondraient aux valeurs $t_{0},$ $t_{1}$ envisagées dans le n^o 349.

357.Revenons aux solutions instables de la première catégorie et aux solutions asymptotiques du premier système représentées sur la figure (11). Je me propose d’établir que l’action est moindre pour $(\mathrm {T} )$ que pour toute courbe fermée infiniment voisine.

Je considère une courbe fermée quelconque infiniment peu différente de $(\mathrm {T} ).$ Cette courbe, que j’appellerai $(\mathrm {T} '),$ est représentée sur la figure (11) par une courbe fermée en trait plein extérieure à $(\mathrm {T} )$ et passant par les points $\mathrm {C}$ et $\mathrm {B} _{3}.$

Bornons-nous d’abord au cas du mouvement absolu. Dans ce cas nous avons le théorème suivant bien connu :

Soient $\mathrm {A} _{1}\mathrm {B} _{1},$ $\mathrm {A} _{2}\mathrm {B} _{2},\,\ldots$ $\mathrm {A} _{n}\mathrm {B} _{n},$ une série continue d’arcs de trajectoires.

Les extrémités de ces arcs se trouvent sur deux courbes

$\mathrm {A} _{1}\mathrm {A} _{2}\ldots \mathrm {A} _{n},\quad \mathrm {B} _{1}\mathrm {B} _{2}\ldots \mathrm {B} _{n}.$

Si ces deux courbes coupent orthogonalement les trajectoires $\mathrm {A} _{1}\mathrm {B} _{1},$ $\mathrm {A} _{2}\mathrm {B} _{2},\,\ldots$ $\mathrm {A} _{n}\mathrm {B} _{n},$ on aura

$(\mathrm {A} _{1}\mathrm {B} _{1})=(\mathrm {A} _{2}\mathrm {B} _{2})=\ldots (\mathrm {A} _{n}\mathrm {B} _{n}),$

en désignant toujours par $(\mathrm {A} _{1}\mathrm {B} _{1})$ l’action correspondant à l’arc $\mathrm {A} _{1}\mathrm {B} _{1}.$

Construisons donc les trajectoires orthogonales des courbes (1). Ces trajectoires que j’appellerai les courbes (2) auront pour équation différentielle

(3)

$\left\{{\begin{aligned}&\left({\frac {d\Phi ^{2}}{dt^{2}}}\!+\!{\frac {d\Psi ^{2}}{dt^{2}}}\right)\,dt\\+&\left({\frac {d\Phi }{dt}}{\frac {d\Phi }{du}}\!+\!{\frac {d\Psi }{dt}}{\frac {d\Psi }{du}}\right)(du\!+\!\alpha u\,dt)+\left({\frac {d\Phi ^{2}}{du^{2}}}\!+\!{\frac {d\Psi ^{2}}{du^{2}}}\right)\alpha u\,du=0.\end{aligned}}\right.$

Pour chaque point du plan, pourvu que $u$ soit assez petit, passe une courbe (2) et une seule. Il ne pourrait en être autrement que si les coefficients de $dt$ et de $du$ s’annulaient à la fois, ce qui ne pourrait avoir lieu que si le déterminant fonctionnel de $\Phi$ et de $\Psi$ par rapport à $t$ et à $u$ s’annulait ; nous avons vu qu’il n’en était pas ainsi.

Les courbes (2) sont représentées sur la figure (11) en trait mixte —··—··—··

Soient $\mathrm {A} _{1}\mathrm {A} _{2}\ldots \mathrm {A} _{5},$ $\mathrm {B} _{1}\mathrm {B} _{2}\ldots \mathrm {B} _{5},$ deux de ces courbes infiniment voisines ; elles interceptent sur $(\mathrm {T} )$ l’arc $\mathrm {A} _{2}\mathrm {B} _{2},$ sur les courbes (1) les arcs $\mathrm {A} _{1}\mathrm {B} _{1},$ $\mathrm {A} _{3}\mathrm {B} _{3},$ $\mathrm {A} _{4}\mathrm {B} _{4},$ $\mathrm {A} _{5}\mathrm {B} _{5},$ sur $(\mathrm {T} ')$ l’arc $\mathrm {CB} _{3}.$

Il me suffit, pour mon objet, d’établir que l’action de $(\mathrm {CB} _{3})$ est plus grande que pour l’arc correspondant $\mathrm {A} _{2}\mathrm {B} _{2}$ de $(\mathrm {T} ).$

Nous avons, en effet,

$(\mathrm {A} _{2}\mathrm {B} _{2})=(\mathrm {A} _{3}\mathrm {B} _{3})$

et, dans le triangle rectangle curviligne infiniment petit $\mathrm {A} _{3}\mathrm {CB} _{3},$

$(\mathrm {CB} _{3})>(\mathrm {A} _{3}\mathrm {B} _{3}).$

On a donc

$(\mathrm {CB} _{3})>(\mathrm {A} _{2}\mathrm {B} _{2}),$

et, par conséquent,

action de $(\mathrm {T} ')>$ action de $(\mathrm {T} ).$

C. Q. F. D.

358.Il reste à voir si le même résultat subsiste encore pour le mouvement relatif.

L’irréversibilité des équations constitue évidemment une différence considérable avec le cas précédent. L’action pour un arc $\mathrm {AB}$ quelconque n’est plus la même que pour le même arc parcouru en sens contraire. D’ailleurs, si une courbe quelconque satisfait aux équations différentielles, il n’en sera pas de même de la même courbe parcourue en sens contraire.

Enfin, les trajectoires orthogonales des courbes (1) ne jouiront plus de la propriété fondamentale que j’ai énoncée dans le numéro précédent. Mais il y a d’autres courbes que je vais définir et qui jouissent de cette propriété. Cela suffit pour que le résultat du numéro précédent subsiste.

Nous avons, au n^o 340, trouvé pour l’expression de l’action

$\mathrm {J} '=\int \left[ds\,{\sqrt {\mathrm {H} _{0}+h}}+\omega '(\xi \,d\eta -\eta \,d\xi )\right].$

Pour simplifier, je poserai ${\sqrt {\mathrm {H} _{0}+h}}=\mathrm {F} \,;$ je désignerai les coordonnées non plus par $\xi$ et $\eta ,$ mais par $x$ et $y$ pour me rapprocher des notations employées dans les numéros précédents et la vitesse angulaire non plus par $\omega ',$ mais par $\omega$ en supprimant l’accent devenu inutile. J’aurai alors

$\mathrm {J} '=\int \left[\mathrm {F} {\sqrt {dx^{2}+dy^{2}}}+\omega \,(x\,dy-y\,dx)\right],$

d’où

${\begin{aligned}\delta \mathrm {J} '=\int {\Big [}\delta \mathrm {F} \,ds&+\mathrm {F} {\frac {dx\,\delta dx+dy\,\delta dy}{ds}}\\&+\omega \,(\delta x\,dy-\delta y\,dx)+\omega \,(x\,\delta dy-y\,\delta dx){\Big ]}\end{aligned}}$

ou, en intégrant par parties,

(4)

$\left\{{\begin{aligned}\delta \mathrm {J} '\!=\!\int &\left[\delta \mathrm {F} \,ds\!+\!2\omega (\delta x\,dy\!-\!dy\,dx)\!-\!\delta x\,d\!\left(\!{\frac {\mathrm {F} \,dx}{ds}}\!\right)\!-\!\delta y\,d\!\left(\!{\frac {\mathrm {F} \,dy}{ds}}\!\right)\right]\\+&\left[\mathrm {F} {\frac {dx\,\delta x\!+\!dy\,\delta y}{ds}}+\omega (x\,\delta y\!-\!y\,\delta x)\right]_{0}^{1}.\end{aligned}}\right.$

L’expression définitive de $\delta \mathrm {J} '$ comprend donc deux parties : une intégrale définie qui doit être prise entre les mêmes limites que l’intégrale $\mathrm {J} '$ et une partie toute connue que j’ai placée suivant l’usage entre deux crochets avec les indices 0 et 1, cette notation signifiant qu’on doit calculer l’expression entre crochets pour les deux limites d’intégration et faire ensuite la différence.

Supposons maintenant que l’on égale à zéro l’expression qui figure sous le signe $\textstyle \int$ dans le second membre de (4). On obtiendra des équations différentielles qui seront précisément les équations du mouvement et auxquelles satisferont toutes nos trajectoires et en particulier les courbes (1).

Ces équations peuvent s’obtenir d’une infinité de manières parce que $\delta x$ et $\delta y$ sont deux fonctions entièrement arbitraires.

Nous pouvons d’abord supposer $\delta x=0$ d’où $\delta \mathrm {F} ={\frac {d\mathrm {F} }{dy}}\,\delta y,$ et notre équation s’écrira, en divisant par $\delta y\,ds,$

(6)

${\frac {d\mathrm {F} }{dy}}-2\omega {\frac {dx}{ds}}={\frac {d\mathrm {F} }{ds}}{\frac {dy}{ds}}+\mathrm {F} {\frac {d^{2}y}{ds^{2}}}\cdot$

Si l’on avait au contraire supposé $\delta y=0,$ aurait trouvé

${\frac {d\mathrm {F} }{dx}}+2\omega \,{\frac {dy}{ds}}={\frac {d\mathrm {F} }{ds}}{\frac {dx}{ds}}+\mathrm {F} {\frac {d^{2}x}{ds^{2}}}\cdot$

Ces deux équations sont équivalentes, comme il était aisé de le prévoir, et, en effet, si on les ajoute après les avoir respectivement multipliées par ${\frac {dy}{ds}}$ et ${\frac {dx}{ds}},$ et si l’on tient compte des relations

${\begin{aligned}\left({\frac {dx}{ds}}\right)^{2}\!+\left({\frac {dy}{ds}}\right)^{2}\!&=1\,;&{\frac {dx}{ds}}{\frac {d^{2}x}{ds^{2}}}+{\frac {dy}{ds}}{\frac {d^{2}y}{ds^{2}}}&=0,\end{aligned}}$

on arrive à une identité.

Si donc nous envisageons les courbes (1), elles satisferont à l’équation (6). Si l’on tient compte de cette équation, la relation (4) devient

$\delta \mathrm {J} '=\left[\mathrm {F} {\frac {dx\,\delta x+dy\,\delta y}{ds}}+\omega \,(x\,\delta y-y\,\delta x)\right]_{0}^{1}.$

Soient $\mathrm {A} _{1}\mathrm {B} _{1},\,\mathrm {A} _{2}\mathrm {B} _{2},\,\ldots ,\,\mathrm {A} _{n}\mathrm {B} _{n}$ une suite continue d’arcs appartenant aux courbes (1) et dont les extrémités $\mathrm {A} _{1}\mathrm {A} _{2}\ldots \mathrm {A} _{n},$ $\mathrm {B} _{1}\mathrm {B} _{2}\ldots \mathrm {B} _{n},$ forment deux courbes continues $\mathrm {C}$ et $\mathrm {C} '.$

Soient $\mathrm {A} _{i}\mathrm {B} _{i},\,\mathrm {A} _{i+1}\mathrm {B} _{i+1}$ deux de ces arcs infiniment peu différents l’un de l’autre. Soient $x,\,y$ les coordonnées du point $\mathrm {A} _{i},$ $x+\delta x,$ $y+\delta y$ celles du point infiniment voisin $\mathrm {A} _{i+1}.$

Soient $\mathrm {J} '$ l’action relative à l’arc $\mathrm {A} _{i}\mathrm {B} _{i}$ et $\mathrm {J} '\!+\delta \mathrm {J} '$ l’action relative à l’arc $\mathrm {A} _{i+1}\mathrm {B} _{i+1}.$

Si $\alpha$ est l’angle que fait avec l’axe des $x,$ la tangente à la courbe $\mathrm {A} _{i}\mathrm {B} _{i}$ qui est une courbe (1), et si les deux courbes $\mathrm {C}$ et $\mathrm {C} '$ satisfont à l’équation différentielle

(7)

$\mathrm {F} (\cos \alpha \,\delta x+\sin \alpha \,\delta y)+\omega \,(x\,\delta y-y\,\delta x)=0,$

on aura

$\delta \mathrm {J} '=0$

et, par conséquent,

$(\mathrm {A} _{1}\mathrm {B} _{1})=(\mathrm {A} _{2}\mathrm {B} _{2})=\ldots =(\mathrm {A} _{n}\mathrm {B} _{n}).$

Les courbes définies par l’équation (7) peuvent donc jouer le rôle que jouaient dans le numéro précédent, les trajectoires orthogonales des courbes (1).

Nous pouvons donc reprendre la figure (11) et supposer que les courbes en trait mixte représentent, non plus ces trajectoires orthogonales, mais les courbes définies par l’équation (7). Nous n’aurons rien à changer à la démonstration.

Un point cependant n’est plus évident. Dans le triangle rectangle infiniment petit $\mathrm {A} _{3}\mathrm {CB} _{3},$ j’avais

$(\mathrm {CB} _{3})>(\mathrm {A} _{3}\mathrm {B} _{3}).$

Le triangle n’est plus rectangle et, d’autre part, j’ai changé la définition de l’action. L’inégalité subsiste-t-elle encore ?

Il serait aisé de voir que cette inégalité équivaut aux conditions (A) du n^o 341 et nous avons vu au n^o 344 qu’elles sont remplies. L’inégalité a donc lieu et notre démonstration subsiste.

En résumé, pour qu’une courbe fermée corresponde à une action moindre que toutes les courbes fermées infiniment voisines, il faut et il suffit que cette courbe fermée corresponde à une solution périodique instable de la première catégorie.

359.Ce que nous avons dit au sujet de la classification des solutions instables en deux catégories nécessite une remarque.

À un autre point de vue les solutions périodiques instables peuvent se répartir en deux classes. Celles de la première classe sont celles pour lesquelles l’exposant caractéristique $\alpha$ est réel, de telle sorte que $e^{\alpha \mathrm {T} }$ soit réel et positif, $\mathrm {T}$ étant la période.

Celles de la seconde classe sont celles pour lesquelles cet exposant $\alpha$ a pour partie imaginaire ${\frac {i\pi }{\mathrm {T} }}$ de telle sorte que $e^{\alpha \mathrm {T} }$ soit réel et négatif.

Dans ce qui précède, nous nous sommes uniquement attachés aux solutions instables de la première classe. Voyons si celles de la deuxième classe peuvent également se répartir en deux catégories.

Nous pourrons poser

$\alpha =\alpha '+{\frac {i\pi }{\mathrm {T} }},$

$\alpha '$ étant réel ; et nous poserons ensuite comme au n^o 346 :

${\begin{aligned}\xi _{2}&=e^{\alpha 't}\varphi _{2},&\eta _{2}&=e^{\alpha 't}\psi _{2},\\\xi _{3}&=e^{-\alpha 't}\varphi _{3},&\eta _{3}&=e^{-\alpha 't}\psi _{3},\end{aligned}}$

où $\varphi _{2},\,\psi _{2},\,\varphi _{3}$ et $\psi _{3}$ sont des fonctions de $t$ qui changent de signe quand $t$ se change en $t+\mathrm {T}$ et qui seront réelles.

Il vient alors

$\zeta (t)=e^{2\alpha 't}{\frac {\xi _{1}\psi _{2}-\eta _{1}\varphi _{2}}{\xi _{1}\psi _{3}-\eta _{1}\varphi _{3}}}=e^{2\alpha 't}\mathrm {G} (t).$

Le numérateur et le dénominateur de $\mathrm {G}$ sont des fonctions de $t$ qui changent de signe quand $t$ se change en $t+\mathrm {T} .$

On est donc certain que ces deux fonctions s’annulent, et par conséquent qu’il en est de même de

$\xi _{1}\eta _{2}-\eta _{1}\xi _{2},\quad \xi _{1}\eta _{3}-\eta _{1}\xi _{3}.$

Ces deux dernières fonctions satisfont à une même équation différentielle linéaire du second ordre dont les coefficients sont des fonctions périodiques de $t$ ne devenant pas infinies, le coefficient de la dérivée seconde se réduisant à une constante. Ces deux fonctions ne peuvent s’annuler à la fois ; car si deux intégrales d’une pareille équation linéaire s’annulaient à la fois, elles ne pourraient différer que par un facteur constant. Or $\zeta (t)$ n’est pas une constante.

Le numérateur et le dénominateur de $\zeta (t)$ s’annulent donc tous deux et ne s’annulent pas à la fois ; donc $\zeta (t)$ ${\big [}$et par conséquent $\mathrm {G} (t){\big ]}$ peut s’annuler et devenir infini.

Toutes les solutions instables en question sont donc de la deuxième catégorie ; à part cela, il n’y a rien à changer à ce qui précède.