Cette page a été validée par deux contributeurs.
90
des théorèmes mécaniques
neveu du poète, dans une série de brochures (1867-1875) que résume l’ouvrage récent de É. Fourrey, Curiosités géométriques (Vuibert et Nony, 1907), p. 319 et suiv. Voici un aperçu de la méthode suivie. 1o Volume du sabot (Hugo dit : onglet) cylindrique. Considérons d’abord un cas spécial (fig. 24) : c’est l’onglet de rayon R, dont la hauteur CD serait égale à la circonférence 2πR. Un plan perpendiculaire à AB détermine le triangle rectangle GEF, semblable à DOC. On a donc 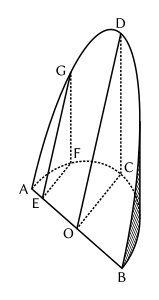
Fig. 24. GFEF = DCOC = 2 π, d’où GF = 2 π EF. Par conséquent, l’aire du triangle GEF (EF × 1/2 GF) = π EF², c’est-à-dire le cercle de rayon EF. Si l’on divise par une série de plans analogues l’onglet en volumes élémentaires, assimilables à des prismes de base EFG, E′F′G′, OCD, etc., la relation ci-dessus permet de remplacer chacun de ces prismes par un cylindre avant même hauteur que le prisme et pour rayons de base les segments EF, E′F′, …, OC, etc. La somme de ces cylindres élémentaires est une sphère de rayon R ; donc aussi le volume V de l’onglet = 4/3 π R³. — Soit maintenant un onglet quelconque ν, de rayon R et de hauteur h. Comparons-le à l’onglet V de même base et de hauteur 2 π R. Les triangles de section ayant même base sont entre eux comme leurs hauteurs ; il en est de même des volumes élémentaires et, par suite, des onglets. Donc v = V h2πR = 2/3 R²h [il est facile de voir que cette expression équivaut bien à celle d’Archimède, puisque le prisme à base carrée du théorème XI-XIV a pour côté de base 2R et pour hauteur h, donc pour volume 4R²h, c’est-à-dire 6 fois l’onglet]. 2o Volume du solide formé par la pénétration de 2 cylindres circulaires dont les bases sont inscrites dans les faces opposées d’un cube. Ce solide est appelé par Hugo équidomoïde à base — ou plutôt à section médiane — carrée ; il construit de même, en envisageant, au lieu d’un cube, un prisme triangulaire, pentagonal etc., des équidomoïdes réguliers à « base » triangulaire, pentagonale, etc. — R étant le rayon du cercle de base, 2h l’arête du cube, l’équidomoïde à base carrée, composé de 8 onglets ayant R pour rayon de base et h

Fig. 24. GFEF = DCOC = 2 π, d’où GF = 2 π EF. Par conséquent, l’aire du triangle GEF (EF × 1/2 GF) = π EF², c’est-à-dire le cercle de rayon EF. Si l’on divise par une série de plans analogues l’onglet en volumes élémentaires, assimilables à des prismes de base EFG, E′F′G′, OCD, etc., la relation ci-dessus permet de remplacer chacun de ces prismes par un cylindre avant même hauteur que le prisme et pour rayons de base les segments EF, E′F′, …, OC, etc. La somme de ces cylindres élémentaires est une sphère de rayon R ; donc aussi le volume V de l’onglet = 4/3 π R³. — Soit maintenant un onglet quelconque ν, de rayon R et de hauteur h. Comparons-le à l’onglet V de même base et de hauteur 2 π R. Les triangles de section ayant même base sont entre eux comme leurs hauteurs ; il en est de même des volumes élémentaires et, par suite, des onglets. Donc v = V h2πR = 2/3 R²h [il est facile de voir que cette expression équivaut bien à celle d’Archimède, puisque le prisme à base carrée du théorème XI-XIV a pour côté de base 2R et pour hauteur h, donc pour volume 4R²h, c’est-à-dire 6 fois l’onglet]. 2o Volume du solide formé par la pénétration de 2 cylindres circulaires dont les bases sont inscrites dans les faces opposées d’un cube. Ce solide est appelé par Hugo équidomoïde à base — ou plutôt à section médiane — carrée ; il construit de même, en envisageant, au lieu d’un cube, un prisme triangulaire, pentagonal etc., des équidomoïdes réguliers à « base » triangulaire, pentagonale, etc. — R étant le rayon du cercle de base, 2h l’arête du cube, l’équidomoïde à base carrée, composé de 8 onglets ayant R pour rayon de base et h
