Page:Poincaré - Leçons sur les hypothèses cosmogoniques, 1911.djvu/128

102

hypothèses cosmogoniques

voisines $\mathrm {E}$ et $\mathrm {E} +d\mathrm {E}$ (fig. 17) ; les normales à $\mathrm {E}$ le long du contour
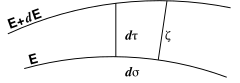
fig.17. d’un petit élément de surface $d\sigma$ définissent, entre ces deux surfaces, un élément de volume

$d\tau =\zeta \,d\sigma ,$

$\zeta$ représentant la distance qui sépare les deux surfaces. La probabilité pour qu’une particule Π soit intérieure à cet élément $d\tau$ est par définition proportionnelle à

$\rho \,d\tau =\rho \zeta \,d\sigma$

de sorte que, si nous restons constamment sur la même surface $\mathrm {E} ,$ nous pouvons dire que la densité superficielle le long de cette surface est représentée par

$\rho '=\rho \zeta \,;$

elle est proportionnelle à $\zeta$, qui visiblement est lui-même proportionnel à

${\frac {1}{\dfrac {d\mathrm {E} }{dn}}}={\frac {1}{\sqrt {\left({\dfrac {d\mathrm {E} }{dx}}\right)^{2}+\left({\dfrac {d\mathrm {E} }{dy}}\right)^{2}+\left({\dfrac {d\mathrm {E} }{dz}}\right)^{2}}}}\cdot$

Restant encore dans le cas de trois dimensions, supposons maintenant que les équations de mouvement admettent deux intégrales

${\begin{aligned}\mathrm {J} _{1}&={\text{const.}},&\mathrm {J} _{2}&={\text{const.}}\end{aligned}}$

L’ensemble de ces deux équations représente une famille de courbes le long desquelles $\rho$ reste constant, tout en pouvant varier d’une courbe à l’autre. Assujettissons $\mathrm {J} _{1}$ à rester compris entre $\mathrm {J} _{1}^{0}$ et $\mathrm {J} _{1}^{0}+d\mathrm {J} _{1}^{0}$, et $\mathrm {J} _{2}$ à rester compris entre entre $\mathrm {J} _{2}^{0}$ et $\mathrm {J} _{2}^{0}+d\mathrm {J} _{2}^{0}$. Nous définissons ainsi un petit tube dont nous appelons $\zeta$ la section droite. Nous pouvons alors prendre des éléments de volume

$d\tau =\zeta \,d\sigma ,$