intervertissant :
Mais (à cause de ΑΣΣΓ = ΣΠΠΜ) :
Donc :
c’est-à-dire :
dans un cône (fig. 5), il mène, par le sommet Α du cône, une parallèle au grand axe ΕΔ de l’ellipse jusqu’à sa rencontre Κ avec un diamètre ΒΓ de la base du cône. Il prend ensuite la perpendiculaire ΕΘ à ΕΔ telle que :
ΕΘ sera le paramètre (ὁρθία). Apollonius démontre (I, 21 ; p. 75, Heib.) que, pour un point Ξ quelconque de l’ellipse, on a :
Heiberg croit que les mots soulignés au texte ont été interpolés 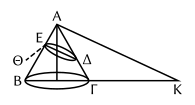
Fig. 5. ou du moins substitués à une phrase autrement rédigée, parce que les termes ὀρθία et πλαγία sont de la création d’Apollonius.
L’égalité (3) peut d’ailleurs être démontrée assez simplement en considérant l’ellipse comme la projection orthogonale d’un cercle (théorème de Stevin). Soient 2a, 2b
