Cette page a été validée par deux contributeurs.
38
des théorèmes mécaniques
2o Quand on coupe un ellipsoïde par un plan passant par son centre et perpendiculaire à son axe, le demi-ellipsoïde ainsi déterminé est double du cône ayant même base et même axe.
Soit l’ellipsoïde K (fig. 4) coupé par un plan 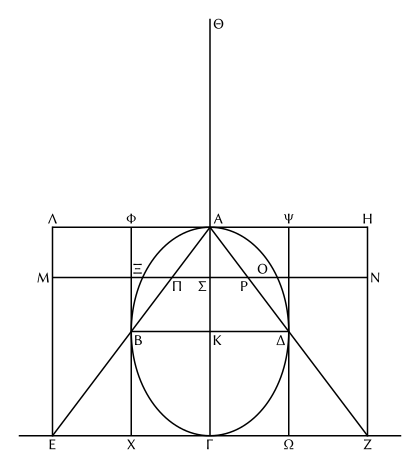
Fig. 4. passant par son axe suivant l’ellipse[1] ΑΒΓΔ, les diamètres ΑΓ, ΒΔ, le centre K ; soit encore le grand cercle de diamètre ΒΔ perpendiculaire à ΑΓ.
Considérons le cône ayant pour base le cercle ΒΔ, pour sommet Α, et prolongeons la surface latérale jusqu’à son intersection, suivant le cercle ΕΖ, avec
- ↑ Archimède dit : « une section de cône acutangle ».
