L’algorithmie de la Logique/03
LOGIQUE ALGORITHMIQUE[1]
TROISIEME PARTIE
Avant-Propos.
Voici une partie de mon travail complètement originale en ce sens que je l’ai conçue et exécutée telle que je la livre aujourd’hui au public, sans avoir eu connaissance des travaux faits dans la même direction notamment en Angleterre. Je l’avais annoncée dans la préface de mon Essai de Logique (1865) ; mais, distrait par d’autres études, j’avais laissé reposer mon projet d’une algorithmie logique lorsque la fondation de la Revue philosophique vint lui fournir l’occasion de paraître au jour. Dans son cadre actuel, elle est nécessairement incomplète, les exigences d’une revue s’opposant à ce que je lui donne de plus vastes développements.
J’ai donc, comme je viens de le dire, laissé de côté pendant un long espace de temps l’examen des questions de logique. C’est ce qui explique pourquoi j’ignorais qu’en Angleterre plusieurs philosophes de la plus haute valeur, principalement Boole, ont cherché, comme moi et avant moi, une algorithmie de la logique. Les travaux de Boole sont analysés longuement dans la Logique du professeur Bain, et je ne les connais que par cette analyse même qui m’a paru très-bien faite. J’en ai déjà dit quelques mots dans la partie précédente. Le reproche capital que je crois devoir faire à Boole, c’est d’être parti de l’idée que l’algorithmie logique ne pouvait être qu’un cas particulier de l’algorithmie algébrique. Aussi ses résultats, obtenus d’une façon parfois curieuse, semblent plutôt être des coïncidences singulières que des déductions absolument exactes. Il se sert, par exemple, du symbole xy pour représenter le concept composé honnête homme ; c’est son droit, sans doute, mais il voit* en cela une multiplication, ce qui est une grave erreur. Il arrive de cette façon à un symbole arbitraire, tel que x 2, qui se présente quand les concepts partiels sont identiques, par exemple, un lépidoptère papillon, ou plus simplement un homme homme. Il suit de là que x² = x, ou que x² − x = 0. Comment, se demande Boole, une pareille égalité peut-elle être satisfaite ? Décomposons-la en facteurs, il vient : x (x − 1) = 0 ; il faut donc l’on ait soit x = 0, ou x − 1 = 0 ; et l’auteur anglais tire de ces formules, comme je l’ai dit, des conséquences très-ingénieuses. Mais il est facile de voir que la première chose à démontrer, c’est la possibilité d’assimiler avec ces formules algébriques les formules logiques[2].
Dans une conférence tenue à Belfast le 17 février 1875, et imprimée depuis, M. John Murphy s’est donné pour mission d’exposer d’une façon claire et substantielle les idées principales d’Hamilton, de Morgan, de Boole. Il a réussi à nous présenter un écrit d’une vingtaine de pages très-concises, extrêmement lumineuses et d’une très-grande portée. Tous ceux qui s’intéressent aux questions de log que feront bien de les lire[3]. Je n’ai à considérer ici que les points où nous nous rencontrons. Nous avons les mêmes notations du jugement sauf une différence dans l’emploi des signes algébriques de s inconnues. Pour lui le jugement s’exprime par x − p = y − q ; ma formule est S − x = P − y. Cette différence, à première vue, indifférente, est cependant capitale ; elle montre que les auteurs qui emploient la première notation ne se sont pas rendu compte de ce qui constitue l’indétermination du jugement. On verra aussi, dans la quatrième partie de mon travail, que ma formule permet de saisir et d’exprimer de la façon la plus nette la cause de l’erreur en général. Signalons encore une autre ressemblance entre les deux systèmes : la manière de noter la négation est de part et d’autre identiquement la même.
Si dans la découverte des formules du jugement et de la négation j’ai été en quelque sorte devancé, il est une partie qui, à ce que j’ai lieu de croire, m’appartient tout entière : c’est la théorie du syllogisme qui est traitée assez imparfaitement chez les auteurs précités et qui n’y donne naissance à aucune proposition générale et pratique. C’est par là que j’ai été conduit à soupçonner d’abord et à reconnaître ensuite avec la plus grande évidence la fausseté des règles aristotéliennes du syllogisme. J’étais presque effrayé de ce résultat, et j’ai été plutôt satisfait que mécontent de constater qu’en ce point aussi je n’étais pas le premier qui eût fait une découverte analogue. Si c’est un grand indice de la vérité d’une loi qu’elle ait été trouvée par deux penseurs qui ne se sont pas communiqué leurs idées, on aura toute raison de croire que l’antiquité, le moyen âge et les temps modernes n’avaient pas dit le dernier mot au sujet des règles du syllogisme.
Enfin, un autre côté original de cette étude est la tentative de faire pour la logique ce qu’Euclide a fait pour la géométrie, et ce qui n’a encore été fait pour aucune science exacte — j’exclus donc par là les œuvres de Spinoza et de ceux qui l’ont imité — à savoir, de la ramener à une série de propositions rigoureusement enchaînées. En cela j’espère avoir des imitateurs qui feront disparaître de mon œuvre les défauts qu’on doit infailliblement y remarquer, qui l’amélioreront sans contredit, et qui la rendront ainsi plus digne d’être offerte aux méditations du public savant.
Ces éléments se divisent en deux chapitres, l’un où l’on traite des principes l’autre de la théorie de leurs applications (cf. Deuxième partie, v, conclusions).
les principes
Découvrir des lois, les vérifier, les démontrer, tel est le but de la science. Pour cela, l’esprit humain passe du particulier au général « — Pierre, Paul, André sont morts, donc les hommes sont mortels — et du général au particulier — les hommes sont mortels, donc Jacques, Jean, Mathieu mourront —. La démonstration des lois réside dans l’accord entre les faits et les conclusions théoriques.
On peut encore dire — car la chose revient au même — que la science compose et décompose les concepts ou les idées que nous nous faisons des choses. Ainsi la botanique cherche à composer le concept de plante, et le décompose à chaque moment de sa constitution pour en vérifier l’exactitude.
La logique a pour objet les concepts en général, et elle recherche les règles de leur composition — logique inductive — et de leur décomposition — logique déductive. En d’autres termes, elle nous enseigne comment on arrive à énoncer des propositions générales et comment on s’assure de leur légitimité. Elle présente ceci de particulier que les règles formulées par elle s’appliquent non-seulement aux autres sciences, mais encore à elle-même.
Nous nous occuperons uniquement de la logique déductive qui a pour objet le concept en tant que formé. Elle doit commencer par en préciser la nature, mais elle ne peut en fournir une définition réelle, puisque c’est de son objet même qu’il s’agit ; elle peut seulement en faire la description, le circonscrire, le délimiter.
I. Du Concept.
1. Définitions. Le concept est un être idéal autour duquel on réunit les qualités communes que l’esprit découvre dans les choses qui constituent un certain groupe, L’extension du concept est l’ensemble des choses auxquelles il est commun ; la compréhension est la somme des qualités que l’esprit a reconnues dans ces choses.
Remarque 1. Le concept diffère de sa compréhension en ceci : dans le concept les qualités constituent une unité. Que le concept ait une extension et une compréhension, c’est là une donnée expérimentale qui sert de point de départ à la logique. Vérifiée sur un certain nombre de concepts, cette proposition est généralisée par hypothèse et sert de fondement aux propositions subséquentes.
Rem. 2. Il y a un certain rapport inverse entre la compréhension et l’extension, mais ce rapport inverse ne peut s’exprimer mathématiquement[4]. Ce qui est néanmoins certain, c’est que la compréhension détermine l’extension et réciproquement. Cependant la comparaison des concepts n’est, en général, possible que sous le rapport de l’extension. L’extension est définie en elle-même et elle a sa raison dans la réalité, tandis que la compréhension doit sa limitation à l’esprit. L’extension du concept homme, par exemple, est parfaitement délimitée ou du moins délimitable ; il n’en est pas de même de sa compréhension. Sans doute, le nombre de ses attributs réels est fixe, mais celui des attributs connus ne l’est pas ; il est susceptible d’augmentation. Chaque comparaison nouvelle que nous faisons entre l’homme et les autres êtres mettant en lumière une nouvelle qualité.
2. Conventions. Si nous représentons par le symbole S (ou P, ou M, etc.) un concept désignant une certaine partie d’un groupe déterminé de choses, nous convenons de représenter par S′ (ou P′, ou M′, etc.) l’autre partie de ce groupe. La réunion de S et de S′ (de P et de P′ etc.) est donc égale au groupe lui-même ; c’est ce que nous exprimons en écrivant : S + S′ = 1. Nous convenons encore de regarder comme équivalentes à cette formule les formules : S = 1 − S′ ; S′ = : 1 − S.
N. B. On entend par choses, tout ce qui existe, a existé ou existera, tant dans le monde intérieur que dans le monde extérieur, et aussi ce qui n’a d’existence que dans l’imagination. L’universalité des choses serait donc l’univers tant réel qu’intelligible, d’où ne seraient exclues ni les monstruosités de la nature, ni celles de l’esprit (utopies, rêves, folies, etc.).
Dans le but de faciliter l’étude de la logique, on peut avoir recours aux figures[5]. Si nous représentons un groupe déterminé de choses
par une surface finie, un cercle, par exemple, et que nous divisions ce cercle par une ligne arbitraire (pointillée dans les fig. 1 et 2) en deux parties proportionnelles aux extensions des concepts S et S′, nous pourrons désigner ces deux parties par les mêmes symboles. Nous emploierons d’ordinaire la figure 1.
3. Déf. De deux expressions unies par le signe + nous pourrons dire qu’elles sont ajoutées l’une à l’autre ; de celles qui sont précédées du signe ‒ nous pourrons dire qu’elles sont ôtées, soustraites, ou retranchées.
Rem. 3. Les formules S + S′ = 1, S = 1 ‒ S′, S′ = 1 ‒ S, sont équivalentes et signifient que tout ce qui n’est pas S est S′ et tout ce qui n’est pas S′ est S. Il n’y faut donc pas voir des additions ou des soustractions comme en mathématique. La forme de la proposition qui, dans le langage, correspond à la formule S = 1 ‒ S′ est négative : S n’est pas S′. Seulement il faut noter que la formule est d’une précision absolue, tandis que la phrase négative est, de sa nature, très-vague. On peut dire du parallélogramme que ce n’est ni un cercle, ni un polygone régulier, ni un carré, ni un trapèze, et aucune de ces négations ne correspond à la formule. Pour rendre possible l’algorithmie de la logique, il faut commencer par faire disparaître cette indétermination. On aura plusieurs fois l’occasion de faire une observation semblable[6].
4. Déf. Le symbole S s’appellera positif, et le symbole 1 ‒ S, négatif. De même S′ sera positif et 1 ‒ S′, négatif.
Quant aux deux symboles S et S′ nous dirons indifféremment que l’un est direct et que l’autre est inverse, ou qu’ils sont inverses l’un de l’autre.
L’indice est ce qui distingue deux symboles inverses. Changer l’indice de S, c’est remplacer S par S′ ; changer l’indice de S′, c’est remplacer S′ par S.
5. Théorème. Le négatif d’un concept est, pour le fond, identique avec l’inverse de ce concept ; en d’autres termes, le négatif d’un direct est un inverse.
Démonstration. Soit S un concept ; son négatif est 1 ‒ S (4) ; or 1 ‒ S = S′ (2) qui est l’inverse de S (4) ; c. q. f. d.
6. Corollaire. Le négatif de l’inverse est identique avec le direct.
7. Théor. Le négatif d’un négatif est identique avec le positif.
Dém. Soit 1 ‒ S un négatif ; en vertu de (4) son négatif peut s’écrire 1 ‒ (1 ‒ S) ; or 1 ‒ S = S′ (2) ; donc 1 ‒ (1 ‒ S) = 1 ‒ S′ ; or 1 ‒ S′ = S (2) ; donc 1 ‒ (1 ‒ S) = S ; c. q. f. d. DEJLBŒUP. — LOGIQUE ALGORITHMIQUE 551
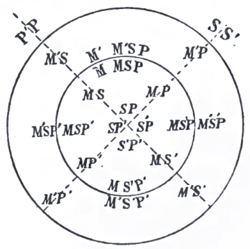
8. Postulat. Étant donnés deux concepts différents S et P tirés d'un même ensemble de choses, c'est-à-dire, soumis aux conditions suivantes (2) : S + S' =1, P + P' = 1, S + S' ==P + P', on peut dire qu'en général S et P auront une partie commune et une partie non commune, ainsi que S et P', S' et P, et S' etP'. C'est ce qui est rendu sensible par la fig. 3.
���Fig. 3.
Rem. 4. C'est là une proposition fondamentale sur les concepts, qui rend possible leur composition et leur décomposition. Cette propo- sition est indémontrable; elle est impliquée dans l'idée que l'on se fait d'un concept. A ce titre, c'est le postulat de la logique déductive<
9. CoNV. Convenons de représenter par SP (fig. 3) ou PS ce qu'il y a de commun entre S et P, et de même par S'P, S'P' et SP' ou bien par PS', P 'S' et P 'S ce qu'il y a de commun entre S' et P, S' et P'> S et P'. De même on désignera par MSP ce qu'il y a de commun entre les concepts M, S, et P; et ainsi de suite.
10. DÉF. Le symbole SP représente un concept qui correspond à une collection de choses parfaitement déterminée. A cause de sa forme, nous lui donnons le nom de symbole double ou de concept double^ par opposition aux symboles ou concepts simples^ tels que S et P. On dira de même de MSP que c'est un symbole ou concept triple.
Au point de vue de la notation, les symboles doubles, triples, etc., porteront en général le nom de symboles ou concepts composés, et les concepts simples qui y entrent, le nom de composants ; mais, au point de vue de l'extension, les composés seront dits concepts spéci- fiques ou espèces, les composants, concepts génériques ou genres.
11. Cor. On peut changer l'ordre des composants. Ainsi MSP = PMS =: SPM, etc.
12. Cor. Si l'extension du genre est nulle, celle de l'espèce est nulle aussi.
13. Cor. Si une espèce (SP) fait partie d'un genre (M), on peut accoler à son symbole celui du genre (c'est-à-dire : SP =MSP). Ré-
�� � 552 REVUE PHILOSOPHIQUE
ciproquement, si ron a des équations SP = MSP, ou S = SP, c'est que SP est une espèce du genre M, et S une espèce du genre P.
14. Cor. Tout, genre peut être décomposé en deux espèces ex- primées chacune par le symbole du genre accolé aux symboles direct et inverse (4) de tout autre genre faisant partie du même groupe de choses. On a donc : S = SP + SP' ; S' = S'P + S'P'; p = SP + S'P; P' = SP' + S'P'.
De même, tout symbole double peut être décomposé en deux sym- boles triples formés de ce symbole double accolé aux symboles direct et inverse d'un troisième concept appartenant au même groupe de choses. On a donc : SP = MSP + M'SP; et par consé- quent : S =. SP + SP' = MSP + M'SP + MSP' + M'SP'.
15. DÉF. Exprimer un composant en fonction de ses composés c'est le développer, l'opération s'appelle développement, et le résultat développée. Réciproquement , ramener une expression formée de composés à une expression plus simple dans sa forme c'est la ré- duire, l'opération s'appelle réduction, et le résultat réduite. Les symboles séparés par les signes +> — i ou =, sont appelés termes.
Rem. 5. Tant que l'on n'est pas familiarisé avec ces notations, on peut se rappeler qu'en algèbre on écrirait : S == SP + SP' = S (P -j- P') = S, puisque P + P' = 1. Bien qu'une pareille transformation soit ici légitime, il faut cependant bien se garder d'assimiler d'une ma- nière générale les formules logiques aux formules algébriques.
16. DÉF. Nous dirons en général d'un concept composé (espèce) qu'il est commun aux composants (genres), et qu'il est exclu des concepts inverses de ceux-ci. Ainsi SP est commun à S et à P et exclu de S' et de P'. Au lieu de commun nous dirons aussi compris ou renfermé.
17. CONV. On peut donner à l'égalité SP + SP' = S (14) la forme : SP = S — SP' ou SP' = S — SP. (comparer 2).
18. Théor. Une expression de la forme SP — SP ou + SP — SP peut se supprimer, c'est-à-dire ne pas s'écrire.
Dém. Si dans la formule SP'=:S — SP (17), on développe S (14, 15), il vient : SP' = SP + SP' — SP, ou bien SP' = SP' + SP — SP ; c. q. f. d.
19. Théor. Au lieu de retrancher (3) les termes de la développée, on peut retrancher la réduite et réciproquement (14, 15).
Dém. Soit une développée SPM + SPM', dont la réduite est SP, il faut prouver que l'on a : S — SPM — SPM' =- S — (SPM +SPM') = S — SP = SP'. Or S = SPM + SPM' + SP'M -|- SP'M' (14), donc : S — SPM — SPM' = SP' M -f- SP' M' (18) = SP' (14) = S — SP (17); c. q. f. d.
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 553
II. Du Jugement.
20. DÉF. On appelle jugement une opération par laquelle, étant donnés deux concepts, on exprime ce qu'ils ont ou n'ont pas de commun. Le jugement est l'énoncé de la relation qu'on établit entre ces deux concepts.
Nous appelons éqitation, égalité, relation ou simplement jugement, l'expression algorithmique d'un jugement. Toute équation se com- pose de deux membres séparés par le signe =. Le premier membre s'appelle sujets le second s'appelle 'prédicat.
Quand le sujet ou le prédicat auront plus d'un terme (15), par exemple, 4 — S ou P — y, nous appliquerons le nom de sujet ou de prédicat grammatical aux symboles S ou P, pour les distinguer spécialement des symboles tels que 1 — S, ou P — y, auxquels nous affecterons la désignation de sujet ou de prédicat logique. De même nous dirons en général concept grammatical en parlant du sujet ou du prédicat grammatical.
21. Théor. Toute équation entre deux concepts S et P peut prendre en général la forme suivante : S — SP' = P — S'P.
Dém, En vertu de (9) et de (17), cette équation revient à SP = SP où les membres sont identiques et expriment ce qu'il y a de commun entre S et P. •
22. DÉF. Toute équation de cette forme où le sujet et le prédicat grammaticaux sont positifs (20 et 4) portera le nom de jugement ou d'équation affirmative.
23. Cor. On peut intervertir les membres d'une équation, c'est-à- dire faire du sujet le prédicat et réciproquement.
Rem. 6. Ce corollaire n'est pas une application particulière d'un principe prétendument général et a priori, par exemple, que l'on peut poser : & = a, si l'on a : a = &. Ce principe est parfaitement démontrable. Si l'on a : a = Z), on peut mettre b à la place de a et a à la place de 6, et si l'on fait cette substitution, il vient \h = a.
24. DÉF. On appelle conversion l'opératiou qui consiste à inter- vertir les deux membres d'une équation. L'équation résultante s'ap- pelle convertie.
25. DÉF. Nous appelons équations originelles les équations affir- matives possibles entre S et S' d'un côté, P et P' de l'autre. Ces équations sont au nombre de huit (cf. rem. 14; prop. 64), et les voici :
Sp_sp! S-SP'=P-ST qp/_sP'! S-SP = P'-S'F
ÔF _ bi- j p _ g,p _ g _ gp, . bl — tst' j p _ g/p. _ s _ SP;
^ ^ ^ M P — SP = S' — S'P': ^ ^ - ^ ^ 1 P' - SP' = S' - ST.
�� � 554 REVUE PHILOSOPHIQUE
26. Cor. Les symboles doubles (10) qui figurent dans les deux membres d'une équation affirmative sont toujours inverses l'un de l'autre (4).
27. Cor. Le concept double qui figure dans Tun des membres d'une équation affirmative est commun au concept grammatical de ce membre, et, par contre, exclu du concept grammatical de l'autre membre (16 et 20). Ainsi dans l'équation S — SP' = P — S'P, par exemple, le symbole double SP' est commun à S, sujet gramma- tical, et exclu de P, prédicat grammatical.
28. Cor. Dans toute équation affirmative le sujet et le prédicat logiques expriment ce qu'ont de commun le sujet et le prédicat grammaticaux (15). Ainsi, étant donnés un sujet K et un prédicat L, le sujet logique devra être KL, c'est-à-dire par conséquent K — KL', et le prédicat logique aussi KL, c'est-à-dire L — K'L.
De même, si l'on donne le sujet K — KL', il est facile de conclure que le prédicat doit être L — K'L.
29. Théor. On peut changer à la fois les indices (4) de tous les concepts d'une équation affirmative.
Dém. Soit l'équation : S — SP' = P — S'P (a), si Ton change les indices de tous les concepts, il vient : S' — S'P =r P^ — SP' (b), ce qui revient à S'P' = S'P', équation originelle (25).
30. Théor. On peut intervertir, c'est-à-dire, faire passer d'un membre dans l'autre, les concepts grammaticaux (20) d'une équa- tion affirmative pourvu qu'on change leurs indices.
Dém. En effet, par cette interversion, l'équation (a) devient iden- tique à l'équation [h) convertie (29, 23, 24).
31. GoNV. Maintenant que la valeur des symboles doubles de l'équation affirmative est connue et déterminée, on peut, sans incon- vénient, les remplacer désormais par les lettres x, y, z, etc. Nous savons, en effet, que dans l'équation S — x = P — y, x est néces- sairement égal à SP' et y à S'P. (28).
Rem. 7. Le choix de ces lettres dont on connaît femploi spécial en algèbre, se justifie par cette considération que, la plupart du temps, le rapport entre le sujet et le prédicat grammaticaux n'est pas connu exactement. Tout ce qu'on sait le plus souvent, c'est que le concept S n'est pas identique au concept P, sans que Ton puisse pré- ciser fextension de ce qui ne leur est pas commun à tous deux (voir plus haut ce que nous disons de la notation de M. Murphy).
32. DÉF. On appelle équation négative, celle où le sujet ou le pré- dicat ou tous les deux ont la forme négative. Si la négation ne se trouve que dans un membre, l'équation est simplement négative ; elle est doublement négative, si la négation est dans les deux membres.
�� � DELBŒUF. LOGIQUE ALGORITHMIQUE 555
33. DÉF. On appelle contraposition la substitution dans une équa- tion d'un symbole négatif à un symbole positif et réciproquement (4). La contraposition est simple si elle n'affecte que le sujet ou le pré- dicat grammatical, elle est double si elle affecte les deux concepts grammaticaux. Les équations obtenues par contraposition sont dites contraposées .
34. Cor. L'équation affirmative fournit deux contrapositions sim- ples et une contraposition double.
S — X = P -T- y ; équation affirmative, 1 — S' — X = P — y; contraposition du sujet, S — x = l — P' — y; contraposition du prédicat, 1 — S' — x= 1 — P' — y; contraposition des deux concepts grammaticaux.
35. DÉF. Dans toute équation, nous appelons membre négatifs celui qui renferme un symbole négatif, et membre positif, celui qui n'en renferme pas.
36. Théor. Tout concept double appartenant à un membre positif d'une équation négative simple (32) exprime ce qui est commun aux concepts grammaticaux des deux membres (cf. 27).
Dém. Soit une égalité négative simple de la forme 1 — S' — x = P — y. Nous savons qu'elle revient à la forme S — x = P — y (2), et que y = S'P (31); y est donc compris dans P et dans S' (16); G. q. f. d.
Lemme 1 . Même démonstration pour l'équation :S — x = l — P' — y.
37. Théor. Tout concept double appartenant à un membre négatif d'une équation négative simple est exclu des concepts grammaticaux des deux membres (cf. 36 et 27).
Dém. Soit une égalité négative simple de la forme : 1 — S' — x = P — y, qui revient à la forme S — x = P — y (2) ; on sait que x = SP' (31); et l'on voit qu'il est exclu à la fois de S' et de P (16) ; c. q. f. d.
Lemme. Même démonstration pour l'équation : S — x =1 — P' — y.
38. Théor. Tout concept double appartenant à un des membres d'une équation négative double , est exclu du concept grammatical de ce membre, et commun au concept grammatical de l'autre membre (cf. 27).
Dém. Soit une égalité négative double : 1 — S' — x = 1 — P' — y, qui revient à la forme S — x = P — y (2) ; on sait que x = SP' et que y = S'P (31); or SP' est exclu de S' et compris dans P', et de même S'P est exclu de P' et compris dans S' (16) ; c. qi. f. d.
1. Le mot lemme servira à désigner à la fois les lemmes et les scolies.
�� � 556 REVUE PHILOSOPHIQUE
RÉSUMÉ DES PROP. 27, 36, 37 et 38. L'équation négative simple exprime la relation entre un sujet et un prédicat grammaticaux au moyen d*un concept double commun à ces deux concepts et figu- rant dans le membre positif, et d'un concept double exclu de ces deux concepts et figurant dans le membre négatif.
L'équation affirmative et l'équation négative double expriment cette même relation au moyen de deux concepts doubles respective- ment compris dans l'un des concepts et exclu de l'autre, ou exclu de l'un des concepts et compris dans l'autre.
39. Théor. Dans toute équation négative simple on peut inter- vertir les concepts grammaticaux sans changer les indices (cf. 30).
Dém. Soit l'équation 1 — S' — x== P — y, elle équivaut à la suivante : S — x =: P — y (2), laquelle peut (30) se transformer en celle-ci : P' — x = S' — y, ou encore (2) en cette dernière : 1 — P — x = S' — y; c. q. f. d.
40. Théor. Dans toute équation négative double on peut inter- vertir les concepts grammaticaux en changeant les indices (cf. 30).
Dém. Soit l'équation :1 — S' — x=^l — P' — y, elle peut prendre successivement les formes suivantes : S — x = P — y (2), puis : P' — X = S' — y (30) , enfin :1 — P — x=l— S— y(2); c. q. f. d.
41. Cor. De la comparaison des propositions 26 et 38, 30 et 40, il résulte qu'il y a la plus grande analogie entre l'équation affirmative et l'équation négative. Par la plus simple des transformations on passe de l'une à l'autre.
42. Théor. Dans toute équation on peut faire passer x et y d'un membre dans un autre en changeant le signe — en signe -\-.
Dém. Soit une équation S — x = P — y, je dis que l'on peut écrire S = P — y + x; car le premier membre de cette équation équivaut à SP + SP' (14) et le second à SP + S'P — S'P + SP' (14, 31), qui, par réduction (18), devient aussi SP 4- SP'; c. q. f. d.
43. Cor. On peut donc écrire aussi : S -j- y = P + x.
44. Cor. Réciproquement, on peut faire passer d'un membre dans un autre un concept double précédé du signe +, pourvu qu'on change le signe + en signe — .
45. Cor. On peut ajouter ou ôter (3) un même concept double aux deux membres d'une équation.
46. DÉF. On appelle discussion 4'examen systématique de toutes les formes que prend une équation par suite de toutes les supposi- tions possibles que Ton fait sur chacun de ses termes, pris isolé- ment, partiellement ou totalement.
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE
��557
��47. On entend par termes variables ceux qui peuvent être l'objet de suppositions différentes.
Dans les jugements ces termes variables sont représentés par x et y. Par conséquent, S — x et P — y sont aussi des termes variables puisqu'ils sont de même nature que x et y (28). Cependant, en Tab- sence d'autres indications, l'expression de variables sera réservée uniquement pour les termes x et y.
48. DÉF. Toute équation peut prendre quatre formes différentes, suivant que les variables y ont toutes deux une extension, ou que x est nul, ou que y est nul, ou que x et y sont nuls tous deux. Ces formes s'appellent modes et seront désignées respectivement par les lettres A, B, G, D, pour les jugements affirmatifs et les négatifs dou- bles (41) par A, B, C, D, pour les jugements négatifs simples.
���Fig. 4.
���Fig. 5.
���Fig. 6.
���Fig. 7.
��Rem. 8. Ces modes correspondent aux positions diverses que les lignes de division peuvent prendre dans le cercle. C'est ce que font voir les quatre figures ci-contre.
��III. Discussion des Jugements affirmatifs*
49. DÉF. Nous appelons complexité ou entrecroisement cette rela- tion du sujet et du prédicat grammaticaux qui correspond au mode
�� � 558 REVUE PHILOSOPHIQUE
A. (S — X = P — y, fig. 4), et nous qualifions de complexe ou entrecroisé le jugement qui l'exprime. Nous pourrons dire aussi qu'un concept entrecroise ou coupe l'autre.
Nous appelons généralité cette relation du sujet et du prédicat grammaticaux correspondant au mode B (S = P — y, fig. 5), et nous qualifions de générique le jugement qui l'exprime. Nous pour- rons dire que le sujet est renfermé , contenu ou compris dans le prédicat (cf. 10).
Nous appelons spécificité la relation du sujet et du prédicat gram- maticaux qui correspond au mode G (S — x = P, fig. 6), et nous qualifions de spécifique le jugement qui l'exprime. Nous pourrons dire que le sujet renferme^ contient ou comprend le prédicat.
Enfin, nous appelons identité^ la relation du sujet et du prédicat grammaticaux correspondant au mode D (S = P, fig. 7), et nous qualifions de identique le jugement qui l'exprime. Nous pourrons dire que les deux concepts coïncident.
La figure suivante peut servir à fournir des exemples de ces diverses relations.
^ irredanffles \ rectangles .
��^eJpulaiù-aiu>\ùTéQalUrs \x isocèles ' scaUn£S^
���A. (S — X = P — y) complexité. Cette relation existe entre les concepts suivants :
1» Triangles rectmigles et triangles isocèles^ car il y a des triangles rectangles qui sont isocèles, mais tous les triangles isocèles ne sont pas rectangles, et tous les triangles rectangles ne sont pas isocèles; enfin, des triangles non rectangles peuvent être non isocèles.
2° Triangles rectangles et triangles scalènes (c'est-à-dire à trois côtés inégaux).
3° Triangles irrectangles (c'est-à-dire acutangles et obtusangles) et triangles isocèles.
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 559
4** Triangles irrectangles et triangles scalènes.
B. (S = P — y) généralité. Cette relation existe entre les concepts suivants :
1° Triangles équilatéraux et triangles isocèles, car tous les triangles équilatéraux sont isocèles, mais tous les isocèles ne sont pas équila- téraux.
2° Triangles scalènes et triangles irrêguliers (c'est-à-dire non inscriptibles dans un cercle, ou dont tous les côtés ne sont pas égaux).
S° Tn3ing\es équilatéraux et tYÎdiïïgles irrectangles. . , '• .•
Le mode B a été appelé générique parce que le sujet est défini au moyen du genre (qui est le prédicat grammatical).
G. (S — X =P) spécificité. Cette relation existe entre les concepts suivants :
1° Triangles isocèles et triangles équilatéraux.
2» Triangles irréguliers et triangles scalènes.
3° Triangles irrectangles et triangles équilatéraux.
Le mode C a été appelé spécifique, parce que le sujet grammatical y est défini au moyen de l'espèce (qui est le prédicat).
D. (S = P) identité. Cette relation existe entre les concepts sui- vants :
1° Triangles équilatéraux et triangles équiangles.
2" Triangles irréguliers et triangles inéquiangles.
50. Cor. Le mode A indique qu'une partie du sujet seulement est renfermée dans l'attribut; et réciproquement, par conversion (24) qu'une partie de l'attribut seulement est renfermée dans le sujet.
Il peut présenter deux cas particuliers.
51. Cor. Premier cas, x = P'; y = S' (fig. 9).
���L'équation : S — x = P — y, devient : S — P' = P — S'. On remarquera que la relation entre S et P est la même que celle qui existe dans la fig. 5 entre S' et P. Cette relation implique que S' est contenu dans P, et que P' est
�� � 560 REVUE PHILOSOPHIQUE
contenu dans S ; elle peut, par conséquent, se décomposer en deux équations du mode B : S' = P — z, et P' = S — z.
Dém. En effet, si nous comparons l'équation S — P' = P — S' à l'équation S — SP' = P — S'P (21), nous voyons que Ton a néces- sairement : P' = SP' et S' = S'P. On pourrait d*ailleurs tirer cette conclusion directement des hypothèses x = P', et y = S', puisque (28), X = SP', et y = S'P. Il s'en suit donc, en vertu de la propo- sition (13), que P' est une espèce du genre S, et S' une espèce du genre P; c'est-à-dire que l'on a : P' = S — z; et S' = P — z; c. q. f. d.
Lemme. Si P est égal à S, et que S' soit égal à P, alors z, c'est-à-* dire SP, est nul, et l'on est ramené au cas de la fig. 7, mode D.
52. Cor. Second cas, x = S; y = P (fig. 10).
���Fig. 10.
L'équation S — x = P — y devient S — S = P — P.
On remarquera encore que la relation entre S et P est de même nature que celle qui, dans la fig. 5, existe entre S et P'.
Cette équation a donc une signification analogue à celle de la précédente, et elle implique deux équations du mode B à savoir :
S:r=P'— z;P = S' — z.
Dém. En effet, puisque x = S, et que x = SP', on a : S = SP', c'est-à-dire que S fait partie du genre P' (13) et qu'ainsi on : a S = P' — z. De même, de ce que y = P et que y = S'P, on a : P = S'P, c'est-à-dire que B fait partie du genre S' (13) et qu'ainsi on a : P = S' — z; c. q. f. d.
Donc toute équation du mode A qui se présente sous les formes S — P'=P — S', ou S — S = P — P pourra se remplacer par des équations du mode B (53).
Rem. 9. Ici l'on touche du doigt la différence qui existe entre Tal- gorithmie de la logique et celle de l'algèbre. Ainsi il ne faudrait pas, se laissant guider par une fausse analogie, s'imaginer que l'on pût tirer l'équation : S — P' = P — S' (51) des équations con-
�� � DELBŒDF. — LOGIQUE ALGORITHMIQUE 561
ventionnelles (2) : S + S' = 4, P -|- P' = 1, par un procédé tel que celui-ci, par exemple : S + S' = P + P', d'où, en faisant passer S' et P' d'un membre dans un autre, et en changeant lès signes : S — P' = P — S'. C'est là une forme d'éqaation qui n'aurait pas de sens si la relation entre les concepts S et P était complexe. Les théorèmes 42 à 45 n'ont, en effet, été démontrés que pour les concepts doubles x et y dont le rôle est bien déterminé dans l'équa- tion du jugement. De même, qu'on n'aille pas croire, en ce qui con- cerne l'équation S — S = P — P (52), qu'elle puisse s'appUquer à deux concepts quelconques, bien qu'en algèbre elle sort d'une vérité absolue. Elle signifie uniquement, et cela en vertu des conventions, que S et P n'ont rien de commun, et que S est contenu dans P' ainsi que P dans S'.
53. Cor. Le mode B indique que le sujet est renfermé tout entier dans le prédicat, et que le prédicat ne coïncide qu'avec une partie du sujet.
L'équation S = P — y n'est susceptible d'aucune variante.
54. Cor. Le mode G indique que le sujet comprend tout entier le prédicat, et que celui-ci ne coïncide qu'avec une partie du sujet.
Le mode G n'est susceptible d'aucune variante.
Au point de vue de la forme, l'équation S — x =:^ P, n'est que la convertie de l'équation S = P — y du mode B. A ce titre, on pou- vait se dispenser de la faire figurer dans le tableau des modes; mais comme elle correspond à une tournure familière du langage (ex : cer- tains hommes sont passionnés), il est indispensable de la maintenir.
55. Cor. Le mode D se dispense de tout commentaire. Il sert de type aux définitions exactes.
Rem. 10. La logique ordinaire ne distingue ' que deux espèces de jugements affirmatifs, les jugements universels correspondant aux modes B et D^ et les jugements particuliers correspondant aux modes A et G. En cela elle s'est laissé tromper par le langage vulgaire qui exprime par une seule et même tournure trois sortes de relations différentes. Exemples : 1" Certains triangles rectangles sont iso- cèles, S — X = P — y; 2« Certains triangles isocèles sont équila- téraux, S — x = P; 3° Certains triangles inéquiangles sont isocèles, S — P' = P — S' (comparer plus loin, rem. 12).
S'il y a des logiciens qui ont cherché, sans la trouver, l'algorithmie de la logique, cette confusion est, pour une grande part, dans leur échec. C'est elle qui, lorsque j'avais la ferme confiance d'aboutir, a; dès que je me suis mis à l'œuvre, le plus entravé mes progrès 1. Elle
1. Après avoir fait disparaître cette confusion, j'étais tellement certain d'a- voir levé le principal obstacle que, une fois en possession de deux ou trois TOME II, — 1876. 36
�� � 562 REVUE PHILOSOPHIQUE
ne se serait pas produite si le langage possédait des tournures propres pour chacune de ces relations.
��IV. Discussion des Jngrements néfiratifs.
Si l'on passe en revue toutes les formes possibles des jugements négatifs simples ou doubles, on trouve qu'elles sont au nombre de douze (cf. rem. 44, prop. 64):
ap)! — S' — x = P— y.
as) S - X = 1 — P' - y.
a) 4 — S' — X =- i — P' — y.
hp)i —S' = P — y.
fes) S = 4 — P' — y.
b)4 — S' = l — P'— y.
cp) 4 — S' - X = P.
es) S — X = 4 — P'.
c)4 — S' — x=l — P'.
dj9)l— S' = P.
ds)S=.i — P'.
d)l — S'=4— P'.
Ces formes, nous les avons désignées par ap, as, a, hp, etc., les lettres a, b, c, d, marquant leur correspondance avec les modes affirmatifs A, B, C, D , les lettres p et s indiquant que tantôt le pré- dicat et tantôt le sujet, ont conservé la forme affirmative.
Si nous nous reportons à la fig. 8, nous pouvons donner comme exemples de ces diverses relations, les couples suivants de con- cepts :
ap) triangles non rectangles ; triangles isocèles,
as) triangles rectangles; triangles non scalènes.
a) triangles non rectangles ; triangles non scalènes.
hp) triangles non irréguliers ; triangles isocèles.
hs) triangles équilatéraux ; triangles non scalènes,
h) triangles non irréguliers; triangles non scalènes.
cp) triangles non équilatéraux ; triangles scalènes.
notations, je ne pris pas la peine de poursuivre mes investigations, et je les suspendis jusqu'à ce que j'eusse le temps et l'occasion de les publier. Quand je me remis sérieusement à ce travail, il y a de cela quelques mois, il ne me fallut pas quinze jours pour composer tout le canevas de la présente algo- rithmie. Quelques logiciens, Hamilton, entre autres, ont avant moi signalé cette confusion, mais ils n'ont vu que deux relations particulières possibles, ils n'ont pas distingué les cas 1 et 3, ce qui est pourtant de la dernière importance.
�� � DELBŒIJF. — LOGIQUE ALGORITHMIQUE 563
es) triangles irréguliers ; triangles non isocèles.
c) triangles non équilatéraux ; triangles non isocèles, dp) tridingles non équilatéraux ; irmngles inéquiangles, ds) triangles équilatéraux; triangles non inéquiangles,
d) triangles non équilatéraux; triangles non inéquiangles.
Rem. 11. On le voit par ces exemples, le jugement négatif ne pré- sente en lui-même pas plus de difficulté que le jugement affirmatif ; il n'y a là qu'un simple changement de notation. Mais il n'en est plus de même lorsque, au lieu d'être noté par des symboles, il est énoncé par le langage. Alors la négation, prise en dehors du texte, est telle- ment vague qu'on ne saurait dire au juste sur quoi elle tombe. Ainsi la phrase : Dieu n'a pas créé le monde en six jours peut signifier que ce n'est pas en six jours que Dieu a créé le monde ; que ce n'est pas Dieu qui a créé le monde ; que ce n'est pas le monde que Dieu a créé, que l'acte de Dieu n'est pas une création, mais^ par exemple^ un arrangement ; et ce ne sont pas là toutes les interprétations possi- bles : ainsi la négation pourrait encore, entre autres, être absolue et porter sur toutes les circonstances à la fois, pour un panthéiste par exemple i. Par conséquent deux choses sont nécessaires : 1» Il faut, quand on traduit en formule algorithmique une phrase négative, bien rechercher quel peut être le rapport du sujet et du prédicat; 2° Il faut, quand on exprime une négation, choisir parmi les tour- nures qu'offre la langue, celle qui semble le mieux appropriée à pré- ciser ce rapport.
C'est faute d'avoir distingué entre le langage et la pensée que les logiciens ont énoncé des règles fausses, inexactes, ou oiseuses. Sans doute la langue peut ne pas présenter assez de ressources, et puis il y a des nécessités littéraires auxquelles il faut obéir. Mais, quand il s'agit de logique et non de beau langage, les douze relations néga- tives rapportées plus haut pourraient, par exemple, se traduire con- ventionnellement comme suit :
ap). Il y a des triangles qui ne sont pas rectangles et qui sont au nombre des triangles isocèles .
oh) Il y a des triangles rectangles qui ne sont pas scalènes, et ré- ciproquement.
a) Il y a des triangles qui ne sont pas rectangles et qui ne sont pas scalènes. hp] Les triangles qui ne sont pas irréguliers sont tous isocèles. hs) Les triangles équilatéraux ne peuvent être scalènes. h) Les triangles qui ne sont pas irréguliers ne peuvent être scalènes.
1 . Voir l'article précité sur la théorie de la négation dans la langue grecque.
�� � 564 REVUE PHILOSOPHIQUE
cp) Parmi les triangles qui ne sont pas équilatéraux, il y a tous les triangles scalènes.
es) Parmi les triangles irréguliers il y a tous ceux qui ne sont pas isocèles.
c) Parmi les triangles qui ne sont pas équilatéraux, il y a tous ceux qui ne sont pas isocèles.
dp) Les triangles qui ne sont pas équilatéraux sont inéquiangles et réciproquement.
ds) Aucun triangle équilatéral n'est inéquiangle et réciproque- ment.
d) Il n'y a pas de triangle non équilatéral qui ne soit inéquiangle et réciproquement.
Si conventionnellement de pareilles tournures étaient adoptées, il n'y aurait plus d'incertitude possible sur la portée de la phrase. On voit par là quel avantage la notation algorithmique présente sur la phrase écrite ou parlée. Cet avantage provient de sa précision ab- solue (cf. rem. 10, prop. 55).
Il y a dans ces tournures, parfois très-compliquées, des artifices de langage en vue d'introduire la négation ; on les remarque surtout quand il a fallu traduire un sujet négatif. Dire, par exemple [d), qu'il n'y a pas de triangle non équilatéral.., revient à dire aucun trian- gle irrégulier, et, en fait, c'est cette expression qu'on choisirait de préférence.
Rem. 12. Cette remarque est essentielle et a la même portée que la remarque 10 : c'est que les jugements où le sujet exclut une partie seulement de l'attribut restent vagues dans le langage ordinaire, à moins de multipher les mots. Je dirai par exemple [as) : les triangles rectangles ne sont pas tous scalènes ; mais cette même tournure est srpplicable à la relation {bp) : Les triangles isocèles ne sont pas tous réguhers ; et à la relation {es) : Les triangles irréguliers ne sont pas tous isocèles. Cependant les rapports entre le sujet et le prédicat de ces trois propositions sont tous différents. En effet, dans {as] il y a exclusion partielle réciproque ; dans (bp) il y a aussi exclusion par- tielle, mais non réciproque, puisque l'attribut est compris dans le sujet; enfin dans {es) il y a exclusion partielle réciproque, mais il n'y a pas exclusion entre les négatifs des concepts, puisque le prédicat est compris dans le négatif du sujet, et que le sujet est compris dans le négatif du prédicat.
Lemme. Les jugements affîrmatifs et les jugements doublement négatifs présentent entre eux la plus grande analogie, et ce que l'on dit des uns, peut, sauf quelques modifications, s'appliquer aux au- tres. Soient, en effet, deux concepts entrecroisés, triangles rec-
�� � tangles et triangles isocèles, le jugement certains triangles rectangles sont au nombre des triangles isocèles, est de la même forme que celui-ci : Certains triangles irrectangles sont au nombre des triangles scalènes; et celui-ci, mis sous forme négative (contraposition double, 32), devient : Certains triangles de ceux qui ne sont pas rectangles sont au nombre des triangles qui ne sont pas isocèles (cf. 41). Nous pouvons donc négliger la discussion de l’équation négative double, en nous en rapportant à celle de l’équation affirmative, mutatis mutandis (48), et nous borner à discuter les jugements négatifs simples ^ .
Lemme. L’équation négative simple peut revêtir deux formes : 1 — S’ — X = P — y, et S — X == 1 — P’ — y. Comme on peut passer de l’une à l’autre par conversion (24), ou par application du théorème 40, nous ne considérerons que les quatre modes possibles de la première, A, B, G, D, correspondant aux équations désignées plus haut par (ap), [bp), (cp) et [dp). Les figures 4, 5, 6 et 7 peuvent servir à en donner l’intelligence.
56. DÉF. Nous appelons diversité, divergence, contrariété et contradiction les relations respectives entre le sujet et le prédicat grammaticaux correspondant aux modes A [i — S’ — x= P — y), B{\—S’= P — X), C (1 — S’ — y = P), et D (1 — S’ = P); et nous qualifions de divers, divergents, contraires et contradictoires les jugements qui expriment ces relations -.
57. Cor. Le mode A signifie que le sujet grammatical S et le prédicat P, bien que y soit commun à l’un et à l’autre (36), et bien que X soit exclu de l’un et de l’autre (37), sont différents pour le reste. En etfet le concept SP, commun à P, est exclu de S’, et le concept S’P', commun à S’, est exclu de P (16). Ex. : triangles rectangles et triangles isocèles.
En dernière analyse, le mode A établit entre les concepts grammaticaux la même relation que le mode A. Ce mode peut présenter deux cas particuliers.
58. Cor. Premier cas, x = P’ ; y -= S’ (fig. 9).
L’équation 1—S’ — x = P— y devient : 1 ~ S’ — P’ == P — S’. Cette relation, comme on peut le faire voir par la même démonstra-
1. Rien ne serait plus aisé que d’être complet et d’examiner à fond tous les cas de l’équation négative double ; mais je préfore être plus court, et laisser quelque chose à faire au lecteur.
2. Les mots contrariété et contraire, qui appartiennent à la logique usuelle, sont mal choisis en ce qu’ils se confondent facilement avec ceux de contradiction et de contradictoire. S’il n’y avait pas certains inconvénients attachés à toute introduction de terminologie nouvelle, j’aurais mis à leur place les mots d’opposition et d’opposé, ou bien ceux d'antagonisme et d’antagoniste. 566 REVUE PHILOSOPHIQUE
tien que précédemment (51), se ramène à des équations du mode B,
59. Cor. Second cas, x = S; y = P (fig. 10).
L'équation 1 — S'-x = P — y devient 1 — S' — S = P — P.
Le sujet et le prédicat grammaticaux ont P de commun (36), et S^ est exclu de l'un et de l'autre (37). Ce cas rentre aussi dans le mode 5 (cf. 52).
Rem. 13. On voit encore ici la différence marquée entre les for- mules logiques et les formules algébriques. On ne pourrait pas, dans l'équation de la proposition 58, supprimer S' dans les deux memVjres et écrire 4 — P' = P ; ni dans l'équation de la proposition 59, écrire P — P = ; on obtiendrait par là des équations dont le sens serait tout différent (cf. rem. 9).
60. Cor. Le mode B exprime que le sujet grammatical S' et le prédicat grammatical P ont un concept commun yr=S'P, mais qu'ils diffèrent sous tous les autres rapports. Ex. : triangles irréguliers et triangles isocèles; le concept commun comprend les triangles iso- cèles non équilatéraux.
L'équation 1 -— S' = P — y ne présente aucune variante.
61. Le mode C exprime que le sujet grammatical S et que le prédicat grammatical P ne se ressemblent qu'en ceci que le concept X, à savoir SP', est exclu de l'un et de l'autre. Ex. : triangles équila- téraux et triangles scalènes. Concept exclu : triangles isocèles non équilatéraux.
L'équation 1 — S' — x = P, ne donne lieu à aucune variante (cf. 54).
62. Le mode D indique que le sujet et le prédicat grammaticaux diffèrent sous tous les rapports, que l'un est tout ce que l'autre n'est pas et réciproquement.
Lemme. La formule 1 — S' = P est, au fond, la même que la formule conventionnelle (2) : 4 — S' — S.
RÉSUMÉ. Entre deux concepts S et P et leurs inverses, il peut y avoir huit équations originelles (25); chacune d'elles est susceptible de revêtir quatre formes affirmatives différentes (48), ce qui fait en tout trente-deux équations affirmatives. A chaque form.e affirmative correspondent trois formes négatives (34), soit quatre-vingt-seize équations négatives. La relation entre deux concepts S et P et leurs inverses peut donc s'exprimer de cent et vingt-huit manières, dont trente-deux affirmatives et quatre-vingt-seize négatives. Ces cent et vingt-huit manières ont été réduites à huit formes principales, quatre affirmatives (49) et quatre négatives (56).
63. DÉF. Le symbole (SP) indiquera une relation principale quel- conque entre S et P.
�� � DELBŒDP. ~ LOGIQUE ALGORITHMIQUE 567
64. Théor. Trois concepts M, S et P peuvent fournir vingt-quatre
jugements différents.
Dém. Les jugements possibles sont exprimés par les symboles (SM), (MP) et (SP), et comme chacun d'eux renferme huit juge- ments différents, il y a en tout vingt-quatre relations possibles entre ces trois concepts pris deux à deux; c. q. f. d.
Rem. 14. A proprement parler, une partie des énoncés des propo- sitions 25 et 64 sont du ressort des mathématiques. En stricte logique, il ne serait pas nécessaire de préciser les nombres ; mais par là l'esprit est satisfait et les limites du champ à explorer sont fixées.
Rem. 15. Si nous jetons maintenant un coup d'œil rétrospectif sur le chemin parcouru, nous voyons que l'algorithmie logique s'est développée par les mêmes procédés que l'algorithmie mathématique : des signes et des symboles pour représenter des idées nettes et précises; des combinaisons de symboles pour désigner des opé- rations; des discussions pour étabUr la signification de certaines combinaisons arbitraires qui ont surgi d'elles-mêmes par suite de suppositions arbitraires aussi, mais naturelles et légitimes. En dehors de cette analogie générale et de quelques ressemblances isolées, les procédés et les règles logiques se distinguent profondément de ceux de l'arithmétique et de l'algèbre. L'on ne voit pas, d'ailleurs, pour- quoi il en serait autrement. Cette observation, nous pourrions la répéter presque à chaque page.
��LES APPLICATIONS
Rem. 16. La théorie du syllogisme correspond en logique à la théorie des équations en algèbre. En effet, l'une et l'autre doivent leur naissance à un problème qui s'énonce à peu près de part et d'autre dans les mêmes termes : Élant données les relations entre certains concepts (entre certaines quantités), exprimer l'un d'eux (l'une d'elles) en fonction explicite des autres.
Si nous approfondissons la comparaison, nous trouverons une analogie plus marquée entre la théorie du syllogisme et celle des équations à deux inconnues. Le syllogisme peut, en effet, se for- muler comme suit : Étant données les deux relations que deux con- cepts, S et P, ont avec un même troisième M, trouver quelle relation ils ont entre eux. Et tout problème à deux inconnues peut s'exposer ainsi : Étant données deux valeurs d'une inconnue en fonction d'une
�� � 568 REVUE PHILOSOPHIQUE
autre inconnue, trouver la valeur de cette première inconnue. En logique, il faut éliminer le troisième terme, le terme moyen; en algèbre, il faut éliminer la seconde inconnue. Mais l'analogie, une fois constatée en ces termes généraux, il faut se garder de l'étendre sous peine de s'égarer. En réalité, en dépit de l'identité des nota- tions et des termes techniques, les deux opérations .sont essentielle- ment différentes : l'une d'elles est un genre de raisonnement spécial; l'autre, le raisonnement dans sa forme la plus abstraite et la plus simple ^
Notons encore ceci, c'est que tous les raisonnements que nous faisons pour établir la théorie du syllogisme supposent déjà cette théorie justifiée, de sorte qu'un traité de logique déductive repose sur un cercle vicieux.
V. Du Syllogisme.
65. DÉF. On entend par syllogisme une opération par laquelle, étant donnés deux jugements appelés j^rémisses, où figure un même concept grammatical, on forme avec les deux autres concepts un troisième jugement appelé conclusion ou conséquence.
Le concept commun aux deux prémisses porte le nom de moyen terme, les concepts non communs, celui de termes extrêmes.
La conclusion établit un jugement entre les termes extrêmes, et ne contient, par conséquent, pas le moyen terme. Nous dirons de celui-ci qu'il est éliminé., et, à ce titre, nous le désignerons souvent sous le nom de terme à éliminer.
Dans la logique usuelle le sujet de la conclusion s'appelle en généralterme mineur., et le prédicat terme majeur; et, conséquem- ment, la prémisse qui renferme ce sujet s'appelle mineure., et celle qui renferme le prédicat majeure. Nous nous servirons parfois de ces mots de majeure et de mineure, mais uniquement pour désigner respectivement la première et la seconde prémisse.
Le problème capital qui sert de point de départ à la théorie du syllogisme peut s'énoncer sous la forme suivante :
66. Problème. Étant données deux prémisses (SM) et (MP), quelle est la forme de la conclusion (SP) qu'on peut en tirer (63)?
Lemme. Ce problème peut présenter trois cas, suivant que, dans les prémisses, le terme à éliminer a le même signe positif ou négatif, ou qu'il a des signes contraires.
1. Je rappelle que ce paragraphe était écrit avant que j'aie connu l'œuvre de
BOOLE.
�� �
67. Théor. Ces trois cas peuvent se ramener à un seul.
1er cas a ; le terme à éliminer est positif. Prémisses : S – x = M – z, et M – u = P – y.
2e cas h ; le terme à éliminer est négatif. Prémisses : S – x = 1 – M – z, et l – M – u = P – y. En remplaçant 1 – M par M′ (2), on retombe sur des prémisses de forme a.
3e cas c ; le terme à éliminer a des signes contraires. Prémisses : S – x = M – z, et 1 – M – u = P – y. En vertu de la proposition 39, cette dernière équation peut s’écrire : 1 – P – u = M – y, ou (2) P′ – u = M – y, ce qui ramène ce cas au premier ; ou bien encore, en vertu de la proposition 30, on peut donner à a première prémisse, la forme M′ – x – S′ – z, d’où : 1 – M – u = S′ – z (2), ce qui ramène ce cas au second ; c. q. f. d.
68. Déf. Nous appelons syllogisme primaire celui dont les prémisses ont la forme a ou b (cf. 41), et syllogisme secondaire, celui dont les prémisses ont la forme c.
Rem. 47. Pour mieux suivre la solution du problème, il faut partir des relations les plus générales qui puissent exister entre les concepts M, S, P, Ces relations sont celles de la complexité (49) entre ces concepts pris deux à deux. Elles sont marquées dans la figure 11.
Les lignes de limitation de SS′ et de PP′ sont restées à leur place. La ligne de limitation de MM′ est une courbe intérieure (cf. fig. 2), et M désigne ce qui est renfermé par cette courbe, M′, le contenu de
la couronne extérieure. Nous continuons à désigner par SP, SM, MP, etc., les concepts doubles communs à S et P, S et M, M et P, etc., et par MSP, M′SP, MS′P, etc., les concepts triples communs à M, S et P, à M′, S et P, à M, S′ et P, etc. (10).
570 REVUE PHILOSOPHIQUELa ligne de limitation de MM' peut prendre différentes positions par rapport à celles de SS' et de PP', ces lignes continuant cepen- dant à s'entrecroiser deux à deux. Les modifications qui en résultent tombent toutes sur les symboles triples tels que MSP, M'SP, etc. Nous allons les énumérer.
69. Théor. Les rapports différents du concept moyen avec les extrêmes, sous la condition que les trois concepts s'entrecroisent deux à deux, sont au nombre de douze (cf. rem. 14, prop. 64). Ils sont déterminés par cette circonstance que ce concept moyen, ou son inverse, ou Tun et l'autre à la fois, coïncident avec un des concepts doubles, formés des deux extrêmes ou de leurs inverses. .
Dém. En effet, a) la ligne de MM' peut prendre une position ana- logue à celle qu'indique la figure 12. Dans ce cas, le concept triple
��Fig. 12.
MSP, à savoir commun à M, S et P, coïncide avec SP, c'est-à-dire que l'on a : MSP == SP. Cette équation signifie que M comprend SP tout entier, et que, par conséquent, nous pouvons écrire : M — X =1 SP (13). Gomme on pourrait avoir de même MSP' =■ SP', MS'P' = S'P', et MS'P = S'P, nous pouvons compter de ce chef quatre modifications.
En outre h) en intervertissant M et M' (même fig., seulement M au lieu de M' et réciproquement) on aurait les quatre mêmes équations, sauf que M' y figurerait au lieu de M, à savoir : M'SP = SP, M'SP' = SP', M'S'P' = S'P', et M'S'P = S'P. Donc, de ce chef, encore quatre modifications nouvelles.
Enfin c) la ligne MM' peut prendre la position marquée par la figure 13. Alors deux concepts triples coïncident avec deux concepts doubles. Dans le cas de la figure, on a : M'SP = SP, et MS'P' = S'P'. On pourrait de même avoir : MSP = SP et M'S'P' = S'P'; ou : M'SP' = SP' et MS'P = S'P, ou enfin ; MSP' = SP' et ^'S'P = S'P. Voilà de ce ch.ef encore quatre modifications nou- velles, ce qui fait en tout douze modifications; c. q. f. d.
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 571
Lemme. De ces douze modifications les quatre dernières offrent cette particularité que deux concepts triples, inverses l'un de l'autre, coïncident avec deux concepts doubles également inverses. Enfin l'on remarque que c'est le symbole du moyen terme qui disparaît.
��Fig. 13.
70. Théor. Étant données deux prémisses S — x = M — z, et M — u = P — y, on peut en tirer une équation de la forme S — x--u = P — y — z.
Dém. En effet, de la majeure (65) on tire : M = S — x -- z? et de la mineure : M = P — y + u (42) ; d'où, par conséquent, (rem. 6, prop. 23) :S — x + z = P — y + u;et de là enfin (44) : S — X — u == P — y — z ; c. q. f. d.
71. Cor. Étant données deux prémisses mises sous la forme : S — X = M — z,M — u = P — y, c'est-à-dire, où le moyen terme figure dans l'une au premier membre et dans l'autre au second, on peut les ajouter membre à membre, et supprimer de part et d'autre le terme à éliminer.
72. Cor. Si dans les prémisses on remplace, x, z, u, y par leurs valeurs respectives M'S,MS',MP',M'P, la conclusion devient :
S — M'S — MP' =: P — M'P — MS'. (a)
Or, par développement (15) on a les égalités (fig. 11) : M'S = M'SP + M'SP' ; MP' = MP'S + MP'S'; M'P = M'PS -j- M'PS'; MS' = MS'P 4-MS'P'.
Substituant ces valeurs dans (a), il vient (19) : {b)
S— M'SP— M'SP'— MP'S— MP'S'=P— M'PS— M'PS'— MS'P— MS'P.
Supprimant de part et d'autre les expressions semblables — M'SP et — MS'P' (45), il vient :
S — M'SP' — MP'S = P — M'PS' — MS'P.
De là (19): S — (M'SP^+ MP'S) = P — (M'PS' + MS'P); et enfin (14) : S — SP' = P — S'P, conclusion qui était à prévoir.
Lemme. Mais, pour obtenir cette conclusion, on a supprimé dans l'un et l'autre membre de l'équation {h) les expressions — M'SP et
�� � 572 REVUE PHILOSOPHIQUE
MS'P'. Ces deux expressions sont inverses : l'une désigne ce qui
est commun à S et à P, mais est exclu du terme moyen M; l'autre, ce qui est exclu des extrêmes S et P, et est compris dan§ M. La première, au point de vue de la coiiclusion qui doit exprimer ce qui est commun à S et P^ ne devait donc pas être retranchée ni de S ni de P ; et c'est ce que signifie la suppression de cette expres- sion négative dans les deux membres. De son côté, l'expression MS'P', désignant ce qui n'est compris ni dans S ni dans P, pouvait sans inconvénient ne pas figurer dans la conclusion, puisqu'elle est inutile; et telle est la signification de sa suppression.
73. Cor. On voit par là que, pour arriver à la conclusion immé- diate de deux prémisses mises sous la forme : S — x = M — z, et M — u = P — y, il suffit d'ajouter M'SP et MS'P' aux deux mem- bres de l'égalité S — x — u = P — y — z (70). La conclusion prend dès lors la forme suivante :
S — X — u + M'SP + MS'P' = P ~ y — z + M'SP + MS'P' .
Quant aux deux termes ajoutés, le premier M'SP élargit la consé- quence en introduisant un concept' commun à S et à P qui était retranché en trop dans x et dans y ; et le second MS'P', bien qu'ex- clu de S et de P, et par conséquent de la conclusion, rend pos- sible la soustraction de z et de u, qui contiennent tous deux ce terme.
74. Lemme. On peut toujours donner aux concepts à ajouter la forme de concepts triples, quand bien même par suite des rapports de M avec S et P, le symbole du moyen terme pourrait ne pas y figurer (69, lemme).
75. Lemme. La conclusion (73) :
S — X — u + M'SP + MS'P' z= P — y — z + M'SP + MS'P' ne rentre par sa forme dans aucun des jugements jusqu'ici connus. A première vue, elle se rapproche du type des jugements complexes (50), mais nous ne pouvons, pour le moment, la déterminer davantage, parce que nous n'avons aucune indication sur l'ensemble des expres- sions qui accompagnent S ou P, et qui, nous le savons, équivalent à SP' et PS'; mais nous ignorons toutefois si elles ont une valeur ou si elles sont nulles, ou si même elles sont compréhensibles. Il nous faut donc chercher à interpréter ce résultat.
76. DÉF. On entend par syllogisme concluant tout syllogisme qui donne lieu à une conséquence interprétable , c'est-à-dire susceptible d'être rangée dans les classes de jugements prédéterminées {49 et 56) ; dans le cas contraire, le syllogisme est non concluant.
77. Théor. Étant donnés trois concepts S,M,P, où le terme à éliminer est M, ils peuvent figurer dans cinq cent et soixante-seize syllogismes différents (cf. rem. 14, prop. 64).
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 573
Dém. Le jugement (SM) (63) donne lieu à huit équations originelles, il suffit d'y remplacer les inverses par les négatifs (5) pour avoir huit jugements différents où figurent les concepts S et M. De plus chacun de ces jugements peut revêtir quatre modes différents (49 et 56) , mais il faut n'en compter que trois, parce que les deux cas où l'un des concepts doubles est nul, proviennent d'une conversion de l'un dans l'autre, conversion déjà comprise dans les équations origi- nelles (54 et 61). Par conséquent le jugement (SM) peut revêtir vingt- quatre formes différentes. Il en est de même du jugement (MP). Par conséquent, les deux prémisses fournissent 24 x 24 = 576 combi- naisons différentes ; c. q. f. d.
Lemme. Si l'on ne s'astreignait pas à la condition que M soit le terme moyen, et si S et P pouvaient tour à tour être pris pour terme à éliminer^ on compterait en tout 576 X 3=1728 syllogismes différents.
Lemme. Ces formes peuvent pour l'étude se réduire considéra- blement, en ne tenant compte ni des conversions ni des contrapo- sitions doubles (41).
78. Théor. On peut ne considérer que trente-deux formes spé- ciales de syllogismes, dont seize primaires et seize secondaires (68).
Dém, Les prémisses d'un syllogisme primaire ont la forme (SM), et (MP) ; comme chacune de ces deux prémisses peut revêtir quatre modes (48) leur combinaison fournit en tout 4 X 4 = 16 syllogismes primaires.
De même les prémisses d'un syllogisme secondaire peuvent se ramener à la forme (SM') et (MP), qui, et pour la même raison, four- nissent en tout 16 syllogismes secondaires ; c. q. f. d.
79. Théor. Des seize formes du syllogisme primaire, douze sont concluantes ; ce sont celles où le terme à éliminer est contenu dans l'un des deux extrêmes.
Dém. Étant données les deux prémisses : S — x = M — z, et M — u == P — y, il faut montrer que si z ou u est nul (54 et 55), quelle que soit d'ailleurs la valeur de x et de y, le syllogisme est concluant.
D'après (73) la conclusion du syllogisme est :
S _ X — u + M'SP + MS'P' = P - y — z + M'SP + MS'P'. (a)
Supposons que z = ; le raisonnement serait le même dans la supposition u = 0.
Or z = S'M (28) ; donc S'M = ; donc S'MP = (12).
Par conséquent l'équation (a) devient :
S _ X — u + M'SP = P — y + M'SP. (6)
Or y est contenu dans P, et à plus forte raison dans P -[- M'SP ;
�� � 574 REVUE PHILOSOPHIQUE
donc le prédicat P — y + M'SP a une extension déterminée ; il en est donc nécessairement ainsi du premier membre.
Quelle est cette extension? On a : y == M'P — M'PS 4- M'PS' (28 et 14) ; donc : P — y + M'SP = P — M'PS' (19 et 18), et réquation (b) devient :
S — X — a + M'SP = P — M'PS'. (c)
Je dis de plus que M'PS' = PS'. En effet : PS' = PS'M + PS'M' (14) ; or si, par supposition S'M = z est nul, PS'M est nul aussi (12) donc : PS' = PS'M'.
Par conséquent l'équation (c) devient :
S — X — u + M'SP = P — PS'. {d)
Il est évident maintenant que toutes les suppositions accessoires sur la nullité de x, y, u, faites isolément ou concurremment deux par deux ou trois par trois, ne changent rien à cette conclusion.
Si l'on fait toutes ces suppositions on trouve qu'elles sont au nombre de douze à savoir :
1, z = 0; 2, z = 0, X = 0; 3, z z:= 0, y = 0; 4, z = 0, x, = 0, y = 0; 5, u ==0; 6, u = 0, x = 0; 7, u = 0, y = 0; 8, u = 0, x;=0, y =0; 9, z = 0, u==0; 10, z= 0, u = 0, x = 0; ll,z = 0, u = 0, y = 0- 42, z = 0, u = 0, X ^ 0, y r= 0; c. q. f. d.
80 Théor. Si le terme à éliminer n'est pas contenu dans l'un des deux extrêmes, c'est-à-dire, par conséquent, s'il les contient ou s'il les coupe, le syllogisme primaire n'est pas concluant.
Dém. Étant données les deux prémisses S — x = M — z ; et M — u = P — y, je dis que si ni z ni x ne sont nuls, quelle que soit d'ailleurs la valeur de u et de y, le syllogisme n'est pas concluant.
D'après (73), la conclusion du syllogisme est :
S — X — u + M'SP H-MS'P' = P — y — z + M'SP + MS'P'. (a)
Supposons à la fois x = 0, et y = 0, c'est-à-dire M 'S =0, et M'P = (28), et, par conséquent (14) M'SP = 0; l'équation (a) de- vient :
S — u + MS'P' == P — z + MS'P'. (e)
Or u =:MP' (28) = MP'S + MP'S' (14); et y = M'P (28) = M'PS' + M'PS' (14);.
Substituant ces valeurs dans l'équation (e) il vient :
S — MP'S=P — S'MP. {fj
Or aucun des deux membres de cette équation ne me fait con- naître son extension : MP'S peut tout aussi bien être contenu dans S que lui être égal, et de même S'MP peut tout aussi bien être égala P qu'y être contenu. La conclusion ne peut donc être interprétée.
Nous avons supposé x et y nuls à la fois ; il est évident que la con-
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 575
clusion reste vraie quand même on accorderait à x, ou à y, ou à tous deux une valeur; il y a donc quatre &as de syllogismes non con- cluants ; c. q. f. d. Passons à la discussion des syllogismes primaires concluants.
81. Théor. Premier cas ; z ou u sont nuls séparément ou con- jointement. La conclusion est complexe.
Dém, Si z seul est nul, la conclusion est (79, d) ;
S — X — u + M'SP = P — PS', équation complexe.
Si z était nul, la conclusion serait :
S~SP' = P — y — z + M'SP, équation complexe.
Enfin, si z et u sont nuls à la fois, la. conclusion est : S — X = P — PS', ou S — SP' = P — y, équations complexes; c. q. f. d.
82. Théor. Deuxième cas : z = 0, et x = 0; ou bien u = et y — ; c'est-à-dire que l'une des deux prémisses est identique. Dans ce cas la conclusion est du même mode que Tautre prémisse.
Démonstration facile.
83. Théor. Troisième cas : z = et y =: 0, c'est-à-dire que dans la majeure (S — x = M) le moyen terme est espèce (54) et que dans la mineure (M — u =:^ P) il est genre (53) . Dans ce cas la conclusion est générique (53).
Dém. On a vu (79) que la conclusion à un moment donné prend la forme (c) : S — x — u + M'SP = P — M'PS'. Or, si y = M'P = (28), il s'ensuit (12) que M'PS' et M'SP sont nuls, donc la- conclu- sion devient : S — x — u = P, équation générique ; c. q. f. d.
84. Cor. Comme P est genre par rapport à M, on peut énoncer le théorème comme suit : Du sujet fS — x) dont s'affirme l'espèce (M) peut s'affirmer le genre (P).
85. Théor. Quatrième cas : u = 0, et x = 0, c'est-à-dire que dans la majeure (S = M — z) le terme moyen est genre, et que dans la mineure (M = P — y) il est espèce. Dans ce cas la conclusion est spécifique (54) .
Dém. Ce cas est au fond le même que le précédent, et la démons- tration identique. La conclusion est : S = P — y — z, équation spécifique; c. q. f. d.
86. Cor. Ce théorème peut s'énoncer comme suit : Ce qui s'af- firme du genre (M) peut s'affirmer de l'espèce (S).
87. Théor. Cinquième cas : Trois des concepts x, y, z et u sont nuls; c'est-à-dire que l'une des prémisses est identique (82). La conclusion sera générique ou spécifique, puisque l'autre prémisse ne peut être que générique ou spécifique.
�� � 576 REVUE PHILOSOPHIQUE
Dém. Ce théorème n'est qu'une combinaison des théorèmes 82, 83 et 84.
88. Cor. Les syllogismes dits par subordination ne sont que des cas particuliers des syllogismes précédents. Soit, par exemple, ce syllogisme : Les homynes so7it mortels, donc quelques hommes sont mortels. Si nous le mettons en formule, il vient : Les hommes sont mortels (M = P — y) ; quelques hommes sont des hommes (S = M — z) ; donc quelques hommes sont mortels (S = P — y — x) ^
���Fig. 14.
��La figure 14 contient tous les cas possibles de syllogismes pri- maires concluants, et la figure 15 contient tous les cas possibles de syllogismes primaires non concluants.
���Dans la première figure on voit que M est contenu dans S. Mais il peut (I) contenir P, ou (II) entrecroiser P, ou (III et IV) être contenu dans P. Or, dans le premier cas, S contient nécessairement P, que la ligne des SS' ait d'ailleurs la forme 1 ou la forme 2. Dans le second
1. M. Laghelier dans la Revue philosophique, 1876, I, 468, a parfaitement démontré que les conclusions dites immédiates sont des cas particuliers des syllogismes ordinaires. (Voir rem. 19.)
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 577
cas, S entrecroise ou contient P, suivant que cette même ligne a la forme 1 ou la forme 2 ; enfin dans le troisième et quatrième cas, S en- trecroise P (1, III), ou contient P (2, III) ou est contenu dans P (IV). Par conséquent, dans toutes les suppositions il y a quelque chose de commun entre S et P.
Dans la figure 15, au contraire, M, on le voit, n'est contenu ni dans S ni dans P, c'est-à-dire qu'il entrecroise ou contient S et P. Or Ton voit que S peut être contenu dans P (I, a, et II, a'), et aussi contenir P, car ce qui se dit de S peut se dire de P, ou entrecroiser P (I, h, et II, h'), ou être exclu de P (I, c, et II, c'). C'est-à-dire, par conséquent, qu'il y a entre S et P tous les rapports possibles.
89. Théor. Des seize formes du syllogisme secondaire douze sont concluantes : ce sont celles où le moyen terme est genre ou espèce par rapport au terme extrême de la prémisse affirmative ou que son inverse est genre ou espèce par rapport au terme extrême de la pré- misse négative ; et quatre sont non concluantes : ce sont celles où le terme extrême ne remplit ni l'une ni l'autre de ces conditions.
Dém. Si l'on a en effet les deux prémisses S — x = M — z , et 1 — M — u = P — y, on peut remplacer la seconde équation par 1 — P — u = M — y (40, 67), et pour que le nouveau syllogisme soit concluant, il faut que z ou y soit nul. On peut aussi remplacer la première équation par 1 — M — x=S' — z (30, 67), et consi- dérer dans le nouveau syllogisme 1 — M ^= M' comme terme à éliminer. Pour qu'il soit concluant il faut que x ou u soit nul. Or, X ou z étant nul, M est genre ou espèce par rapport à S, sujet de la proposition affirmative; et, y ou u étant nul, 1 — M ou M' est genre ou espèce par rapport à P, prédicat de la proposition négative.
On démontrerait de la même façon la seconde partie de ce théo- rème.
Nous ne discuterons pas ce théorème, parce que, d'un côté, cette discussion est facile et tout-à-fait analogue à la précédente, et que, de l'autre côté, nous voulons épargner le plus possible au lecteur la fatigue qui doit résulter pour lui de cette accumulation d'abstrac- tions .
RÉSUMÉ. Les théorèmes 79, 80 et 89 renferment toute la théorie du syllogisme. Barbara et Baroco peuvent être mis à la réforme.
90. Lemme. a la rigueur, on peut dire que de deux prémisses il y a toujours une conclusion à tirer, fût-ce celle qu'on n'en peut rien conclure.
Rem. 18. Les théorèmes 79, 80, et 89 peuvent servir, étant donnés trois concepts S, M et P, et leurs rapports, à dire combien de syllogismes concluants on pourrait en former. Car on ne peut TOME II. — 1876 37
�� � 578 REVUE PHILOSOPHIQUE
prendre pour terme moyen que le concept qui est dans une certaine relation à l'égard de Tun des deux autres. Deux concepts peuvent quelquefois être pris indifféremment pour moyens termes , mais jamais les trois à la fois. Nous nous contentons d'indiquer cette con- séquence sans la développer.
Rem. 19. Dans les syllogismes primaires non concluants, les prémis- ses, avons-nous vu, ont la forme M — x = P — y, ou M — x = P (80), c'est-à-dire que, traduites en langage vulgaire, elles donnent des jugements que la logique ordinaire appelle _particuiiers. (Cf. rem. 10, prop. 55).
On connaît la règle formulée par les logiciens que de deux juge- ments particuliers on ne peut rien conclure. Nous venons de donner la démonstration de, ce principe. Mais en même temps cette démons- tration fait voir en quoi ce principe est sujet à restriction. Il faut, en effet, que ce soit le terme moyen qui figure ou du moins puisse figurer comme sujet dans les jugements particuliers. Car si les pré- misses ont les formes S— x =M, etM — x = P — y ou F, qui se traduisent toutes deux par des jugements particuliers, le syllogisme est concluant (79). Ainsi le syllogisme suivant : Quelques triangles sont isocèles, quelques triangles isocèles sont équilatéraux , donc quelques triangles sont équilatéraux, est parfaitement légitime ; ainsi que cet autre plus trivial, mais plus facile à saisir : Quelques hommes sont chauves, quelques chauves portent perruque, donc quelques hommes portent perruque.
Si donc l'on donne cette prémisse : quelques parallélogrammes sont rectangleSy où rectangles soit le moyen terme, il est certain a priori que, quelle que soit dans la seconde prémisse la relation de ce terme avec l'autre extrême, le syllogisme sera concluant. Si je dis : quelques rectangles sont losanges (complexité), ou quelques rec- tangles sont carrés (spécificité), ou quelques rectangles ne sont pas des losanges (diversité), ou quelques rectangles ne sont pas carrés (divergence), je puis parfaitement conclure que quelques parallélo- grammes sont des carrés ou des losanges, ou que quelques parallélo- grammes ne sont pas des losanges^ ou ne sont pas des carrés.
L'erreur des logiciens provient de ce qu'ils ont confondu lindéter- mination du langage avec l'indétermination de lai pensée. Pour que la conclusion devînt évidente à travers le voile du langage, il suffirait qu'il y eût une forme spéciale de proposition pour indiquer cette re- lation d'un sujet à un prédicat qui y est renfermé, par exemple : Les parallélogrammes comprennent , entre autres,, tous les rectangles. C'est ainsi que l'on dit : Les singes anthropomorphes comprennent, entre autres, les chimpanzés.
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 579
On pourrait objecter que les propositions telles que quelques hommes portent perruque sont, à proprement parler, des jugemeiits immédiats, et non des conclusions obtenues par raisonnement, et que le prétendu syllogisme est artificiel. Je crois qu'en cela on aurait raison. Aussi je ne mentionne ce cas que parce que l'on fait figurer dans les logiques ordinaires les syllogismes par subordina- tion qui ressemblent beaucoup moins encore à des raisonnements (cf. 88).
Rem. 20. La logique ordinaire énonce aussi cette proposition que l'on ne peut rien conclure de deux prémisses négatives. Nous voyons par les propositions 67 et 68 que cette assertion est fausse : si les deuxp rémisses ont la forme S — x = l — M, etl~M — u=:P — y, quelle que soit d'ailleurs la valeur de x, u et y, le syllogisme est con- cluant. Ces deux prémisses ont les formes que nous avons désignées par es et ap. Si donc j'ai comme majeure et comme mineure ces deux propositions : Il n'y a pas, de triangles non isocèles en dehors des triangles irréguliers (S— x =^ \ — M, M = isocèles, S = irréguliers) ; certains triangles 7%on isocèles sont rectangles (1 — M — x = P — y, P = rectangles), je puis tirer la conclusion que certains triangles irréguliers sont rectangles (S — x = P — y). Ici encore, ce qui a trompé les logiciens, c'est l'indétermination de la négation dans le langage. C'est ce que nous allons mettre en évidence.
Supposons qu'il y ait entre les concepts sensible et inseiisihle ainsi qu'entre ceux de vivant et d'inerte l'opposition contradictoire marquée par les équations M=:l — M'^etP = i — P'; et soit ce syllogisme concluant :
Les animaux sont sensibles; S := M — z.
Les êtres sensibles sont vivants ; M = P — y.
■ Donc les animaux sont vivants . S = P — z — y .
Nous pouvons contraposer simplement la majeure et la mineure, et il viendra :
Les animaux ne sont pas insensibles; S = l — M' — z.
Les êtres qui ne sont pas insensibles
sont vivants ; 1 — M' = P — y.
Donc les animaux sont vivants. S = P — z — y.
On soutiendra peut-être que la mineure n'est pas négative. Nous la rendrons négative par une contraposition double.
Les animaux ne sont pas insensibles ; S = 1 — M' — z.
Les êtres non insensibles ne sont pas
inertes; 1 — M' = 1 — P' — y.
Donc les animaux ne sont pas inertes. S = 1 — P' — z — y.
�� � Voilà certes deux prémisses négatives. Mais on remarquera que la mineure est doublement négative, et l'on pourrait désirer que la négation y fût simple et tombât sur le prédicat. C'est ce que nous allons faire :
Les animaux ne sont pas insensibles; S = 1 — M' — z.
Les êtres insensibles ne sont pas vivants; M' — y = 1 — P.
ou bien (39) : P — y = 1 — M'.
Donc les animaux sont vivants. S =: P — z — y.
Chacun observera tout d'abord que ce syllogisme n'a pas l'air juste; et il aura droit de s'en étonner puisque chacune des propositions a conservé son sens primitif. Gela provient de ce que la mineure n'est pas explicite, en d'autres termes, ne nous apprend pas le rapport exact qu'il y a entre insensible et vivant. Au point de vue du langage elle correspond en effet aux deux formules M' = 1 — P, et M' — y=:l — P. Mais comme c'est la seconde formule seule qui exprime le rapport véritable, à savoir qu'il n'y a d'êtres non vivants que parmi les êtres insensibles, si pour la mineure je choisis une tournure correspondant exactement à cette idée , la conclusion de- viendra évidente :
Les animaux ne sont pas insensibles ;
Il n'y a que des êtres insensibles qui ne soient pas vivants ;
Donc les animaux sont vivants.
Rem. 21. Enfin la logique usuelle énonce cette dernière règle : On ne peut rien conclure d'une majeure particulière et d'une mineure négative. Cette règle est encore fausse ; et c'est ce qu'il est facile de faire voir en peu de mots. En effet, le théorème 89 nous apprend que si l'inverse du terme moyen est genre ou espèce par rapport au terme extrême de la prémisse négative, le syllogisme sera concluant. Si nous choisissons une pareille mineure (67) il nous sera libre de choisir quelle majeure nous voulons. Soit donc une mineure de la forme 1 -— M — z = P, ou M' — z = P qui remplit la condition précisée ; il est certain qu'avec une majeure particulière de la forme S — x=M — u, je tirerai la conclusion légitime : S — X = P' — z — u. Il suffît pour le voir de donner à la mineure la forme M = 1 — P — z (39) puis d'ajouter les deux prémisses (71 j et de remplacer 1 — P par P'.
Voici un exemple de cette sorte de raisonnement :
Quelques triangles isocèles sont rectangles ; S — x = M — z.
Les triangles rectangles ne sont pas équilatéraux ; M' — u = P.
Donc quelques isocèles ne sont pas équilatéraux. S — x = P'— z — u. DELBŒUF. — LOGIQUE ALGORITHMIQUE 581
Ainsi encore est valable ce syllogisme :
Quelques parallélogrammes sont rectangles j S — x — M.
Les rectangles ne sont pas des quadrilatères
à angle rentrant ; 1 — m — y = P.
^ Donc quelques parallélogrammes ne sont pas
des quadrilatères à angle rentrant. S — x = l— P' — y.
De même que le suivant :
Quelques parallélogrammes sont rectangles; S — x = M.
Les rectangles ne sont pas des quadrilatères
à angle aigu; 1 _ M == P.
Donc quelques parallélogrammes ne sont pas
des quadrilatères à angle aigu. S — x = 1— P.
Rem. 22. Toute algorithmie est une espèce de machine qui, une fois réglée pour un but déterminé, travaille d'une manière incons- ciente et amène infailliblement le résultat que l'on a en vue. Quand un calculateur résout les équations d'un problème d'algèbre ou de géométrie analytique, il ne se demande pas quelle est la signification des transformations qu'il fait subir à ses formules; il sait seulement que telle transformation est légitime, et cela lui suffit. Ainsi encore les épures de géométrie descriptive qui constituent aussi, par con- vention, une espèce de langage algorithmique , sont exécutées machinalement d'après des règles déterminées, et il n'est pas besoin qu'avant de mettre la main à l'œuvre, on se représente dans l'espace le résultat final. Ainsi en est-il de l'algorithmie logique. Le logicien qui sait la manier, du moment qu'il a traduit en formules les pré- misses, en tire la conclusion, sans se préoccuper de la manière dont la pensée pouvait naturellement y arriver i.
Soient données, par exemple, ces deux prémisses : Quelques hommes sont athées (S — x = M), quelques savants ne sont pas athées (P — y = 1 — M — z). On voit qu'elles peuvent donner lieu à un syllogisme concluant, puisqu'elles appartiennent à un syllo- gisme secondaire, et que le moyen terme M est espèce par rapport au terme extrême delà prémisse affirmative (89). Si l'on tire la conclusion en remplaçant la majeure par la formule suivante qui en découle légitimement (30) : 1 — M — x ^ 1 — S, et que l'on élimine 1 — M, par addition (71) il vient :P— y = l— S — z, ou bien (39) :S — y — x = l — P — z, formule qui, traduite à son tour en langage ordinaire, équivaut à la conclusion : Quelques hommes ne sont pas savants.
A première vue, on ne comprend pas comment cette conséquence
1. Comparer plus haut la note qui contient le jugement de M. J. Venn sur le troisième caractère de la logique de Boole.
�� � 582 REVUE PHILOSOPHIQUE
peut être renfermée dans les prémisses; et pourtant rien n'est plus certain. C'est ce qui se voit dès que Ton fait disparaître T in détermi- nation de la mineure. Sa formule nous apprend qu'il y a des savants athées et des savants non athées, et réciproquement qu'il y a des athées qui ne sont pas savants. Donc, puisque tous les athées sont hommes, il y a des hommes qui ne sont pas savants.
L'algorithmie a ainsi permis de tirer, par un procédé très-simple et surtout infaillible, une conclusion que la logique ordinaire ne dé- couvre qu'avec peine, ou que même elle ne parviendrait pas du tout à découvrir, si l'esprit humain ne sortait pas des règles étroites ùo elle tend à l'emprisonner.
��VI. De r emboîtement des jug^ements.
91 . DÉF. Nous entendons par jugement emboîtant celui dont le sujet ou le prédicat est lui-même un jugement. Ce dernier est dit emboîté. La relation entre le jugement emboîtant et le jugement emboîté s'appelle emboîtement.
Les jugements peuvent être simplement , doublement , triple- ment, etc. , emboîtants ou emboîtés. Exemples :
1 . La Ugne droite est le plus court chemin entre deux points.
2. Ce jugement (la proposition 4) est une définition.
3. L'assertion 2 est une erreur (par exemple, pour celui qui attribue à la proposition 1 les caractères d'un théorème).
4. Cette affirmation 3 a été démontrée.
5. L'U démonstration est évidente.
La proposition 5 est un jugement quadruplement emboîtant, et, par rapport à lui, la proposition 1 est quadruplement emboîtée.
Le sujet et le prédicat d'un jugement emboîtant peuvent être tous deux des jugements emboîtés. Exemple : Dire que des parallèles sont des droites ayant même direction, revient à dire que des droites qui ont même direction sont parallèles.
Généralement, le jugeaient emboîté est sujet.
Rem. 23. Parmi les prédicats qui peuvent être attribués à un jugement, il en est qui présente un intérêt particulier. Le jugement correspond ou ne correspond pas à la réalité, et, d'un autre côté, l'esprit lui accorde ou lui refuse son adhésion.
En fait, la coïncidence ou la divergence entre le jugement et la réalité est encore une conception de Tesprit; mais Fesprit n'admet pas que le réel ne soit pas, bien qu'il concède que ce qui lui appa- raît comme vrai puisse être faux. Je puis être certain que le monde
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE '583
^st soumis à des lois, et conserver des doutes sur la réalité des lois découvertes. En tant donc que distinct du réel, le vrai n'est, après tout, que le vrai pour nous, autrement dit, le vraisemblable . C'est là un point très-important que nous avons examiné dans la pre- mière partie de ce travail. Nous y avons vu que la vérité objective n'est pas la même chose que la vérité subjective, bien que, en fait, la première se traduise toujours par la seconde.
92. DÉF. Au point de vue de la vérité objective, la relation entre le sujet et le prédicat est conçue comme ne pouvant pas ne pas être, auquel cas elle est absolue^ ou comme pouvant ne pas être, auquel cas elle est potentielle. Elle peut aussi être conçue comme correspon- dant à la réalité, et dans ce cas elle est dite réelle, ou bien comme n* ayant qu'une existence fictive, dans ce cas elle est dite imaginaire.
De là, toute relation se range dans l'une des quatre classes sui- vantes : le nécessaire, Vimpossihle, le contingent, le possible. C'est «e que montre la figure 16.
��Fig. 16.
Le nécessaire {n] c'est ce qui est réel d'une façon absolue,, c'est ce qui ne peut pas ne pas exister. Vimpossible (i), c'est ce qui est imaginaire d'une façon absolue, ipar conséquent, ce qui ne peut pas exister. Le contingent (c) est un réel potentiel, c'est ce qui existe, mais pourrait ne pas exister; et le possible (p) est un iynaginaire potentiel, c'est ce qui n'existe pas, mais pourrait exister.
93. Cor. A et P sont des concepts contradictoires (56), ainsi que R et I; et l'on a : A = 1 — P; R == 1. — L On a aussi : n = AR; i=z AI; e^PR; p = PL
Rem. 24. La logique ordinaire appelle modalité la manière dont est conçue la relation entre le sujet et le prédicat, et elle a divisé de ce chef les jugements en apodictiques, assertoires et problématiques. Les jugements apodictiques comprennent ceux qui posent la relation comme nécessaire et ceux qui la posent comme impossible. Nous ferons donc une distinction ultérieure.
�� � 584
��REVUE PHILOSOPHIQUE
��94. DÉF. Au point de vue de la vérité objective, les jugements se divisent en apodictiqiies. répulsifs, assertoires et problématiques *.
95. Théor. On peut conclure du nécessaire à l'absolu ou au réel; du possible au fictif et au potentiel; de l'impossible au fictif et à l'absolu; du contingent au réel et au potentiel.
Dém. Nous avons n = AR (93); or A et R peuvent s'affirmer de ce dont s'affirme n (84); c. q. f. d.
Même démonstration pour les autres parties du théorème.
Rem. 25. Dans la logique ordinaire, on dit souvent que l'on peut conclure du nécessaire au contingent et au possible. G est une confusion dans laquelle Aristote s'est gardé de tomber. Ce qui est nécessaire n'est ni possible ni contingent, car, qui dit possible ou contingent, dit qui peut ne pas être, et le nécessaire ne peut pas ne pas être.
96. DÉF. Au point de vue de la vérité subjective (de la vraisem- blance) la relation entre le sujet apparaît comme vraie ou fausse (est vraisemblable ou invraisemblable) suivant que l'esprit lui accorde ou lui refuse son adhésion; comme certaine ou douteuse y suivant que l'esprit n'apporte pas ou apporte de l'hésitation à accor- der ou refuser cette adhésion. De là, toute relation se range dans l'une des quatre classes suivantes : évidence, absurdité, probabilité, improbabilité. C'est ce que montre la figure 17.
���Fig. 17.
��Vévident (e) c'est ce que l'esprit reconnaît comme certainement vrai, c'est ce qu'on ne peut pas ne pas admettre. L'absurde (a) c'est ce que l'esprit reconnaît comme certainement faux, c'est ce qu'on ne peut pas admettre. Le probable (p), ou plutôt l'admissible ou V ac- ceptable, est ce que l'esprit penche à reconnaître comme vrai, c'est ce
1. Les mots apodictiques et assertoires sont mal formés. Le premier signifie seulement démonstratifs, et le second peut s'appliquer à toute espèce de juge- ment ou d'assertion. Mais je n'ai pas voulu substituer de nouveaux noms à ces termes consacrés par le temps.
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 585
qui se rapproche du vrai; Vimprohahle (i), ou mieux, Vinadmissihle ou Vinacceptahle est ce que Tesprit penche à reconnaître comme faux, c'est ce qui se rapproche du faux.
N. B. Les mots admissible, inadmissible, etc., étant plus subjectifs que ceux de probable et d'improbable, seraient à préférer.
97. Cor. V et F sont des concepts contradictoires (56) ainsi que G et D; et Ton a:V = l--F;G=l — D. Ona aussi : e = GV; a=:GF;p = DV; i = DF.
98. DÉF. Au point de vue de la vérité subjective, les jugements se divisent en évidents, absurdes, acceptables ou inacceptables.
99. Théor. De l'évident on peut conclure au certain et au vrai; de l'absurde, au certain et au faux; de l'acceptable au douteux et au vrai; de l'inacceptable au douteux et au faux.
Même démonstration que plus haut (95).
Rem. 26. Qu'on puisse conclure de l'évident au vrai, et de l'ab- surde au faux, cela s'admet sans difficulté. Mais, au premier abord, il semble qu'on ne puisse conclure du probable au vrai ou de l'im- probable au faux. G'est qu'alors on fait rentrer la signification de vrai et de faux dans celle de véritable et de mensonger, ou encore de réel et de fictif, tandis que, en vertu de la définition que nous avons choisie, vrai signifie vraisemblable, et faux, invraisemblable. Le vrai, avons-nous dit, est ce qui provoque l'adhésion de l'esprit; si cette adhésion est absolue, le vrai est évident; si cette adhésion n'est pas accordée sans quelque réticence, le vrai n'est que probable ou acceptable. Une définition analogue a été donnée du faux. Ainsi, un jugement acceptable ou probable, provoquant l'adhésion de l'es- prit se présente comme vrai, et un jugement inacceptable comme faux. Il ne faut donc pas attribuer ici, ne l'oublions pas, aucune valeur objective aux termes vrai ou faux. Une erreur palpable peut, pour certains esprits, avoir tous les caractères d'une vérité évidente.
Rem. 27. On peut généraUser cette remarque. Les mots du lan- gage ordinaire ont une valeur précise pour celui qui les emploie, et cette valeur peut fort bien ne pas être saisie par les autres ; c'est ce qui fait bien souvent que Paul ne voudrait pas affirmer ce que sou- tient Pierre. On connaît la légende de ce puissant aimant qui tient suspendu en l'air le tombeau de Mahomet. Gomme l'a démontré M. Plateau, la chose en soi est impossible, le tombeau devant se trouver en pareil cas dans un état d'équilibre instable. Mais si je ne connais pas la démonstration, je pourrai dire que la chose est pos- sible, bien que je conçoive en même temps qu'elle puisse être impos- sible. Donc, quand je dis : c'est possible, je veux simplement dire que je ne vois actuellement pas de raison qui puisse me faire rejeter
�� � 586 REVUE PHILOSOPHIQUE
la possibilité du fait; mais je n'affirme pas que, d'après moi, un tombeau aurait la puissance d'être suspendu de cette façon. Possible, en un mot, signifie, dans ce cas, admissible. En conséquence, et cette observation a été déjà faite nombre de fois, quand on traduit les phrases en formules, il faut avoir soin de bien peser la valeur de chacun des mots, et voir s'ils sont employés dans leur sens logique. Un cas à noter pour cette signification du mot possible, nous est fourni par la théorie des syllogismes 7ion concluants. On peut dire, en effet, après Télimination du terme moyen, que toutes les rela- tions entre S et P sont possibles (89). En fait une seule est réelle, et, par conséquent, possible. Mais cette expression est ici prise dans un sens objectif bien déterminé, et dès lors rien n'empêche de l'em- ployer.
100. DÉF. Deux jugements emboîtants qui ont le même sujet et dont les prédicats sont contradictoires (56) sont dits contradictoires.
101. Théor. De la vérité d'une proposition on peut conclure à la fausseté de sa contradictoire.
Dém. On a : V = 1 — F ; et F = 1 — V (97); donc V = 1 — (1-V) ; c. q. f. d. (cf. 7).
102. Cor. De la fausseté d'une proposition on peut conclure à la vérité de sa contradictoire.
103. Cor. Si une proposition est réelle, sa contradictoire est fictive j si une proposition est absolue, sa contradictoire est poten- tielle.
��VII. Des jugements récurrents.
104. DÉF. Nous appelons jugement récurrent celui qui peut être à lui-même son propre objet. Exemple : Toute proposition est démon- trable; donc, si cela est vrai, cette proposition est elle-même dé- montrable.
Rem. 28. Ces jugements sont intéressants à étudier. On en ren- contre fréquemment dans les œuvres de propagande ou de polé- mique. Vous hrez, par exemple, qu'il ne faut s'attacher à aucun système — et l'auteur de cet axiome ne s'aperçoit pas qu'il énonce en ce peu de mots un système. Vous entendrez un penseur s'écrier avec conviction : Plus de théorie ! des faits, encore des faits, toujours des faits ! — Mais n'accorder d'autorité qu'aux faits, n'est-ce pas une théorie ?
Parmi les jugements récurrents quelques-uns peuvent être vrais; mais il en est qui sont nécessairement faux; d'autres ne veulent
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 587
rien dire du tout Nous donnons quelques exemples pour chaque cas.
105. CoNV. Étant donnés deux concepts S et P, il y a entre eux une certaine relation qui peut prendre un nombre déterminé de formes équivalentes. Nous représentons par (R) ces formes équiva- lentes exprimant la relation exacte entre S et P, et par (R') toutes les autres relations qui sont, par conséquent, inexactes. (R) + (R') = 1, représente donc toutes les relations possibles entre S et P.
,106. Théor. Si nous représentons par S et P, le sujet et le pré- dicat grammatical (20) d'un jugement récurrent, pour que ce juge- ment soit admissible, il faut que l'on ait (R) =i P — x.
Dém. Ona S =P; or cette relation que l'on peut représenter (105) par (R) fait partie du sujet S en vertu de la définition (104) ; on a donc (R) = S — X. Éliminant S entre ces deux équations (71) il vient: (R)= P — x; c. q. f. d.
Voici quelques applications :
I. On doit et Von peut démontrer toute vérité.
Représentons par T (R) tous les jugements vrais possibles; et soit D (initiale du mot démontrable) le prédicat; on a T(R) = D. Or c'est là un jugement qui est lui même compris dans T(R), de sorte que, si nous le représentons (R^), on a : (RJ = T(R) — x ; de là (17) : (R,) = D — X. Donc cette proposition elle-même doit et peut se dé- montrer; elle n^implique aucune contradiction, elle peut être vraie.
IL On ne peut pas démontrer toutes les vérités.
Des jugements compris dans T(R) les uns sont démontrables et les autres ne sont pas démontrables, en d'autres termes, quelques propo- sitions seulement sont démontrables; on a donc rT(R) — y = D (a). Mais c'est là aussi un jugement compris dans T(R) ; si nous le représentons par (R^) nous aurons (R^) = T(R) — x (b). Or entre les deux prémisses (a) et (b) on ne peut éliminer T(R) qui n'est contenu dans aucun des deux extrêmes (79). Par conséquent on ne peut dire si (R), à savoir la proposition en question, est parmi les démontrables ou les indémontrables. Elle n'implique donc pas de contradiction i.
III. Il n'y a pas de règle sans exception.
Les règles sans exception sont toutes comprises dans les jugements spécifiques (S = P — y) ou identiques (S = P). Les jugements né- gatifs se ramènent aussi à ces deux formes. Appelons (R) ces sortes de règles sans exception. La proposition à examiner peut se formuler comme suit : T (R) == F — y ; tout (R) est taux. Or c'est là aussi une relation de la forme (R) ; appelons-la (RJ, et nous aurons :
1. Voir ce que nous disons, Première partie, IL
�� � 588 REVUE PHILOSOPHIQUE
(R,) == T (R) — X. Éliminant, il vient : (RO = F — - x — y. Donc (RJ est faux ; or, s'il est faux, sa contradictoire R' est vraie (101) ; il y a donc des règles sans exception, quand ce ne serait que cette asser- tion même : il y a des règles sans exception. La proposition en question est donc nécessairement fausse.
IV. Tout est vrai.
C'est la thèse du fatalisme matérialiste, car les idées prétendument fausses, tirant leur origine des lois inéluctables de la matière sont tout aussi légitimes que les idées prétendument vraies i.
On a donc : T (R) = V — x ; mais aussi il est permis d'écrire : T (R) = F — y (a); et cette assertion, étant comprise dans T (R), est vraie ; on a donc par élimination de T(R) : V — x = F — y, c'est- à-dire que certaines propositions vraies sont en même temps fausses; et parmi ces propositions se trouve celle que nous examinons. Au lieu de la proposition (a) nous pouvions aussi écrire T (R) = F — x; et l'on concluait alors que V = F , c'est-à-dire, admettre que tout est vrai, c'est identifier le vrai et le faux, et admettre que tout est faux.
N. B. Les mots vrai et faux sont pris ici dans leurs sens objectif (Voir rem. 23 et 26).
V. Tout est faux.
C'est la thèse du scepticisme.
On a donc : T (R) = F — y. Mais c'est là une relation que nous pouvons représenter par (R^), et nous avons (Rj) = T (R) — x ; donc (Rj) = F — y — x, c'est-à-dire que cette thèse est fausse. Elle aboutit donc à une conséquence analogue à celle que nous avons obtenue dans les n°' lil et IV. Cependant il y a une distinction à faire. Ceux qui soutiennent les propositions III et IV admettent la légiti- mité du raisonnement, admettent qu'il existe des règles auxquelles ils soumettent leur thèse; tandis que le sceptique nie la légitimité de la raison. En conséquence l'argumentation dans III et IV est ad hominem, tandis que dans V elle n'atteint pas l'adversaire.
VI. La vérité est relative aux temps et aux lieux. C'est la thèse de l'éclectisme.
Toute proposion n'est vraie qu'en son temps et en son lieu, c'est- à-dire est provisoire : T(R) = P -— y. Or c'est là une proposition (Rj) qui elle-même doit être provisoire : (R^) = P — y — x, et qui, par conséquent, est vraie en certains temps et certains lieux, mais est fausse en d'autres temps et en d'autres lieux. Si l'éclectisme regarde le système qu'il énonce comme étant la vérité du moment, il n'est pas en contradiction avec lui-même, mais il reconnaît par
1. Voir plus loin comment nous expliquons l'erreur.
�� � DEtBŒUP. — LOGIQUE ALGORITHMIQUE 589
là même qu'il ne possède pas la vérité éternelle, et qu'un autre système peut renfermer la vérité .
Rem. 29. On voit que les conclusions tirées de ces divers exem- ples sont de natures différentes. La proposition I n'implique pas de contradiction, ni la proposition II non plus, avec cette nuance que celle-ci i^ewt ne pas en impliquer. La proposition III est nécessaire- ment fausse. Les propositions IV et V suppriment tout raisonnement, car tout raisonnement repose sur la distinction fondamentale entre le vrai et le faux. Enfin de la proposition VI on a conclu que les affirma- tions des éclectiques, si elles étaient vraies, ne le seraient que provi- soirement, et qu'elles sont ainsi soumises aux mêmes fluctuations que celles des autres systèmes combattus cependant par eux.
Il y aurait peut-être à chercher la solution de ce problème général : A quelles conditions un jugement récurrent est-il nécessairement faux ou nécessairement vrai? Je ne sais pas encore si ce problème, ainsi posé, est susceptible d'une solution autre que celle du théorème 106.
Rem. 30. On ne peut clôturer cette algorithmie de la logique sans dire un mot des prétendus jugements disjonctifs et hypothétiques.
La logique ordinaire, on le sait, appelle disjonc^i/" tout jugement delà forme : S est A ouB ; S est A ouB ou G. Exemple : Un triangle est irréguher ou réguUer ; un triangle est équilatéral, isocèle ou scalène.
Ce ne sont pas là, à proprement parler, des jugements simples. C'est une forme abrégée de langage pour exprimer une série de juge- ments, par exemple : quelque S est A (SP == A — x) ; quelqu'autre S est B (SP' = B — y), et ces deux sujets partiels constituent la to- talité de S (SP + SP' = S). Ainsi : Quelques triangles sont irré- guliers ; quelques autres triangles sont réguliers ; les triangles qui ne sont pas réguliers sont irréguUers, et réciproquement.
Si l'on a affaire à une triple alternative, le jugement est le résumé des cinq jugements suivants : SPM = A — x ; SPM' = B — y ; SP' = G — z ; SPM + SPM' = SP; SP' + SP' = S'.
On appelle hypothétique tout jugement de cette forme : Si S est A, S est B. Exemple : Si ce triangle a ses côtés égaux, il a aussi ses angles égaux. Ge n'est là qu'une appUcation au sujet S de la proposition que A est B ( A — B, ou A = B — x) et du corollaire 84. En outre la propo- sition S est A est mise sous forme de jugement emboîtant (91) : S est A est possible ; donc S est B est possible. Ainsi : Un triangle équilatéral est équiangle ; ce triangle peut être équilatéral (jugement probléma- tique) ; il peut donc être équiangle (conclusion problématique).
L'apologiste de Socrate vient de faire le portrait de son héros; il
1 . Voir dans l'article précité de M. J. Venn l'application des formules de BooLE aux jugements disjonctifs. C'est on ne peut plus curieux.
��(
�� � 590 REVUE PHILOSOPHIQUE
a fait voir que c'est un sage dans toute la force du mot, et conclut en disant : Comment un tel homme peut-il avoir corrompu la jeu- nesse? Voilà une phrase très-simple qui est un jugement emboîtant (il est impossible que Socrate ait corrompu la jeunesse) conclusion de tout le plaidoyer. Cette conclusion pouvait se mettre sous la forme hypothétique : Si donc Socrate est un sage, il ne peut avoir cor- rompu la jeunesse? La forme change-t-elle la nature du jugement? La phrase primitive était interrogative ; elle aurait pu être exclamalive ; a-t-on jamais songé à faire une catégorie de jugements interrogatifs, exclamatifs, etc?
Disons-le une dernière fois : il faut distinguer entre la forme logique et la forme grammaticale. La logique procède par proposi- tions types, facilement réductibles en formules : Les hommes sont mortels^ Pierre est un homme ^ donc Pierre est mortel. Mais le lan- gage peut revêtir ces types de mille façons différentes : Les hommes sont mortels, donc^ si Pierre est homme, il est mortel. — Si les hommes sont înortels, comme Pierre est un homme, il est mortel. — Pierre est mortel^ parce qu'il est homme et que les hommes sont mortels. — Pierre est homme ou il ne l'est pas ; sHl est homme, il est mortel, car les hommes sont 7nortels. Voilà, sans compter les enthy- mèmes, un certain nombre d'expressions diverses ayant une portée identique. Au fond c'est toujours le même syllogisme.
��QUATRIEME PARTIE
DE l'utilité de la LOGIQUE DÉDUCTtVE.
Quelle est TutlUté de la logique algorithmique? Cette question est complexe. Pour la résoudre, il faut, comme en toutes choses, pro- céder par analogie. C'est, en effet, un cas particulier d'une autre question beaucoup plus vaste ; quelle est l'utilité d'une algorithmie en général ? demande qui peut, à son tour, se spécialiser, puisqu'elle s'appUque à l'arithmétique et à l'algèbre, et à toutes les sciences algorithmiques en un mot. Quelle est donc l'utilité de l'arithmétique et de l'algèbre ?
I. — De rntUité- de l'arithmétique et de l'algrèbre.
Supposons qu"il s'agisse de résoudre ce problème :
Pierre a la moitié du nombre des noix que possède Paul. Il dit à
�� � DELBŒUF. — LOGIQUE ALGORITHMIQUE 591
celui-ci : Donne-m'en 10, nous en aurons autant l'un que l'autre. Gomlâen ont-ils de noix chacun ?
L'arithmétique nous permettra-t-elle de résoudre ce problème? Non. Résoudre des problèmes n'est pas l'office de l'arithmétique. L'arithmétique fait des opérations, des additions, des multiplica- tions, etc., rien d'autre. D'ailleurs elle ne s'occupe ni de Pierre, ni de Paul, ni de leurs uoix, cela est tout-à-fait en dehors de son cadre. Mais celui à qui le problème est proposé se dira sans doute qu'on peut le résoudre au moyen de l'arithmétique en ce sens qu'il suffit de faire certaines opérations pour avoir la réponse. Mais quelles peuvent être ces opérations, c'est ce que Farithmétique ne peut lui apprendre.
Comprendre que le problème revient à renonciation d'un pro- blème d'arithmétique, c'est déjà un grand point : on peut alors cher- cher à le ramener à une forme générale. Soit proposé en effet cet autre problème :
Jacques a le double de l'âge de Laurent. Si Jacques était né 10 ans plus tard et Laurent 10 ans plus tôt, ils auraient tous deux le même âge. Quel âge ont-ils l'un et l'autre?
Au point de vue ordinaire, la question n'est pas la même que la précédente ; mais au point de vue arithmétique, elle est absolument identique. Pourquoi? parce que l'une et l'autre sont une application de cette troisième question qui en est pour ainsi dire la formule :
Deux nombres sont doubles l'un de l'autre ; si l'on retranche 10 du plus grand et que l'on ajoute 10 au plus petit, les résultats sont égaux. Quels sont ces deux nombres ?
Or celui qui ne parvient pas à ramener un problème à sa formule arithmétique a beau connaître l'arithmétique, il ne saura pas l'ap. pliquer ; c'est un manchot à qui on a remis un ciseau dont il est in- capable de se servir.
Voilà le problème ramené à une forme générale. Sommes-nous au bout? Non; il est encore indispensable que l'on devine par quel genre d'opérations on déterminera les inconnues. Nous sommes donc toujours en dehors de l'arithmétique, et cette science ne nous sera utile que du moment que nous aurons fait subir au problème à ré- soudre cette dernière transformation :
Déterminez deux nombres dont l'un soit égal à la somme de 10 et de 10, et dont l'autre soit égal au double de cette somme.
Mais avant d'en arriver là que de raisonnements un enfant ne doit- il pas faire! Je dis un enfant : ce n'est pas qu'un mathématicien exercé ne se livre aussi à la même argumentation ; seulement il la fait plus vite, d'une manière plus ou moins inconsciente et comme
�� � d’instinct. En résumé donc, l’arithmétique ne tranche que la plus petite partie du problème ; on peut même dire que tout le problème est résolu quand il a été ramené à la dernière forme. Une machine peut faire le reste. Et, en fait, le calculateur n’est au surplus qu’une machine vivante.
Ce qui vient d’être dit de l’arithmétique s’applique parfaitement à l’algèbre. L’algèbre trace les règles pour la résolution des équations, règles faciles, expéditives et commodes ; mais la difficulté c’est de former ces équations, de mettre, comme on dit, les problèmes en équations. A quels efforts de raisonnement ne faut-il pas se livrer pour mettre en équations ce problème, par exemple :
Simon peut faire un certain ouvrage en 10 jours ; Jérôme n’y consacrerait que 8 jours. En combien de temps pourraient-ils l’achever s’ils travaillaient ensemble ?
Ou cet autre, dont l’énoncé est si simple et la solution si compliquée :
Un puisatier, a mis 10 jours à creuser la moitié d’un puits (dans un terrain homogène) ; quel temps mettra-t-il pour creuser l’autre moitié ?
On peut le répéter, la mise en équations c’est, en définitive, presque tout, et la résolution des équations bien peu de chose. Mais c’est énorme pourtant si l’on songe que, sans l’algèbre, la résolution de bien des problèmes serait presque impossible.
L’algèbre rend des services qu’il est impossible le plus souvent à l’arithmétique de rendre. Le système algorithmique de l’algèbre s’applique à des notions plus élevées ; c’est une machine plus puissante, plus riche en effets variés, en résultats inattendus. Elle décide des questions devant lesquelles l’arithmétique s’arrête, analysée. Le calcul différentiel et intégral vient à son tour avec ses méthodes plus efficaces encore prêter au géomètre une force considérable. Et à mesure que la machine se perfectionne, elle peut exécuter des ouvrages de plus en plus difficiles, de plus en plus compliqués, de plus en plus délicats.
II. De l’utilité de l’algorithmie logique.
De quel secours peut donc être l’algorithmie de la logique en tant que symbolisation de la logique déductive naturelle ? Comme on l’a vu, et comme on l’a pu du reste prévoir, c’est tout ce qu’il y a de plus élémentaire. Par conséquent, elle ne peut servir qu’à résoudre des questions d’une grande simplicité. Quand le raisonnement est ramené à une série de syllogismes, elle est en état, sans aucun doute, de signaler les conséquences possibles, ou d’indiquer rapidement et sûrement la vraie conclusion. Mais la difficulté réelle, devant laquelle on vient se buter, consiste à traduire le raisonnement en syllogismes concluants. Comment, par exemple, faire subir cette transformation à une argumentation par laquelle j’attaquerais comme irrationnel le principe d’une autorité humaine infaillible et supérieure à la raison, devant un adversaire qui prétendrait que la raison elle-même implique la croyance à une autorité infaillible ? C’est ainsi, en effet, que les croyants à l’infaillibilité procèdent et sont contraints de procéder à l’égard des incrédules. Je pourrais objecter, si je veux plaider la cause de ces derniers, que vouloir établir rationnellement l’impuissance de la raison est une contradiction manifeste ; qu’exiger de la raison que par un acte purement rationnel elle signe son abdication, c’est lui demander une chose impossible ; qu’il ne peut y avoir entente pour l’adoption d’un point de départ commun entre celui qui, pour le moment, ne croit qu’à sa raison et celui qui la regarde comme une faculté trompeuse. Tous ces enthymêmes peuvent être justes ; on sent, pour ainsi dire, d’instinct qu’ils peuvent être admis comme vrais par les uns, regardés comme faux par les autres. C’est ainsi que l’on résout par tâtonnement ou par intuition des problèmes parfois très-compliqués. Mais la formule où est-elle ? où en trouver les éléments ? Essayons toutefois de la donner.
Tout ce qui est rationnel est croyable, c’est-à-dire, s’impose à la raison (R = C - x) ; (1)
L’infaillibilité d’une personne humaine élue est, par hypothèse, une idée rationnelle (I = R - y) ; (2)
Donc l’infaillibilité est croyable (I = C - y - x = C - z) ; (3)
Or l’infaillibilité n’est pas identique avec la raison, elle lui est supérieure ; elle comprend donc autre chose que la raison, que nous désignerons par le terme de non-raison ; ou encore, l’infaillibilité et la non-raison sont des concepts entrecroisés qui ont un certain domaine de commun (I - u = R′ - v) ; (4)
Éliminant I entre (3) et (4), on en tire (79) que des choses autres que rationnelles sont croyables (R′ - v = C - z - u = C - l) ; (5)
De (5), en vertu de la proposition (30), on tire que certaines choses rationnelles sont incroyables (R - v = C′ - l) ; (6)
Si maintenant nous comparons (2) et (6), comme ces propositions donnent lieu à un syllogisme non concluant (80), on voit qu’il est possible (voir rem. 27, prop. 99) que l’infaillibilité, bien que rationnelle par hypothèse, soit comprise parmi les choses incroyables (I - v = C′ - y - t), (7)
proposition qui est en contradiction avec la proposition (3).
Par conséquent, affirmer que la raison humaine postule l’infaillibilité d’une intelligence humaine supérieure à la raison c’est énoncer un jugement récurrent qui implique contradiction.
Supposons notre démonstration exacte : qui ne voit que le travail principal a consisté à poser les équations ? Celles-ci trouvées, l’algorithmie a pu permettre d’effectuer un peu rapidement certaines transformations, par exemple, celle de (5) en (6) ; mais, si l’on n’avait pas écrit l’équation (4), tout le raisonnement était arrêté. De plus il a encore fallu faire un choix parmi les transformations possibles et les éliminations, et dans ce choix l’algorithmie n’était pour rien. De sorte qu’au total les services pratiques que l’algorithmie a rendus sont de chétive importance. C’est comme si, pour effectuer l’opération 6 X 7, on recourait à la table des logarithmes.
Mais il ne faut pas perdre de vue que, sous ce rapport, son sort est intimement lié à celui de la logique formelle déductive. Si l’algorithmie logique n’a pas d’utilité pratique, la logique formelle d’Aristote et de Kant n’en a pas davantage ; on peut même dire qu’elle en a beaucoup moins, puisque, ainsi que nous l’avons vu, elle contient des erreurs considérables, malgré la valeur qu’elle s’attribue (cf. Première partie, V).
III. De l’origine de l’erreur.
Mais l’algorithmie, entre autres avantages théoriques, nous donne la clef de la solution d’une question très-grave qui nous reste à résoudre. Comment l’erreur a-t-elle pu se glisser dans une pareille science ? En quoi consiste l’erreur ? Si l’erreur a sa raison d’être, est-elle encore l’erreur ?
L’erreur consiste à n’accorder aucune existence à l’inconnu, en d’autres termes, à poser comme nul ou n’existant pas ce que l’on ne connaît pas. Telle est la définition et en même temps la cause de l’erreur (cf. Troisième partie, jugements récurrents, IV). Elle consiste, pour employer les formules, à poser, au lieu d’une équation qui doit renfermer des x ou des y, une équation qui ne les contient pas. L’erreur, en un mot, a sa source dans une vue inconsciemment incomplète des choses.
De là vient qu’un raisonnement erroné peut être juste ; seulement il n’est pas conforme à la réalité. La méthode à suivre doit donc être de s’assurer, avant de poser une équation, qu’il n’y a pas une inconnue échappant pour le moment aux regards et devant donner à l’équation sa vraie physionomie. L’erreur provient d’un excès de confiance ou de présomption ; la vérité se livre à ceux qui se défient d’eux-mêmes et qui la cherchent sans parti pris.
Ainsi, à côté de la logique déductive viçnt se placer la logique inductive. Celle-ci nous apprend à bien appliquer les règles et elle n’a pas de règles elle-même, dans le sens propre du mot ; car celles qui lui servent de guides sont toutes d’induction. Comme la logique déductive, la logique inductive est le produit d’un cercle vicieux (cf. rem. 16, Troisième partie). Mais de même que les sens des animaux inférieurs se sont de plus en plus perfectionnés, et sont devenus, par exemple, l’odorat du chien, la vue de l’aigle, l’ouïe du chat, de même nos ancêtres nous ont transmis, et à notre tour nous transmettrons à nos descendants un cerveau de plus en plus antipathique à l’erreur ; notre intuition de la vérité sera plus pénétrante, nous apprendrons à rester en place plutôt qu’à nous engager dans une voie aventureuse, à faire même un pas en arrière plutôt que de courir les hasards d’une course aveugle.
Un mot encore. Je ne voudrais pas répondre que ce travail sur l’algorithmie de la logique ne contînt pas. des lapsus ou des lacunes regrettables. J’ai dû trop souvent revenir sur mes pas pour parfaire une démonstration incomplète, je me suis trop souvent aperçu que je glissais sur une mauvaise pente pour ne pas montrer un peu de circonspection. Peut-être mes essais, tout imparfaits qu’ils sont, feront à quelque amant des loisirs studieux chercher des voies plus courtes pour arriver à la démonstration des théorèmes sur les syllogismes. Il arrivera ainsi à supprimer des définitions, des propositions et des lemmes intermédiaires ; et, d’autre part, il tirera de nouvelles conséquences, et fera une application plus étendue de la méthode. Oserais-je croire que c’est là une œuvre réservée à l’avenir ? Une chose cependant me paraît actuellement acquise : c’est qu’il est possible de trouver pour la logique un système de notations qui fasse de cette science une sœur de l’arithmétique et de l’algèbre ; de lui donner plus de fixité, de précision et d’exactitude ; de la soustraire à diverses causes d’erreur ; de lui permettre enfin de fournir des solutions sûres et promptes. Ce résultat ne me paraît pas tout-à-fait à dédaigner, et m’autorise à compter sur l’indulgence de mes lecteurs.
- ↑ Voir la Revue du 1er septembre et du 1er octobre.
- ↑ Il y a sans doute de la témérité à juger un philosophe d’après un simple résumé. Le Mind d’octobre 1876 contient sur ce logicien un article de M. J. Venn, d’où j’extrais les passages suivants (p. 480 et passim) qui viennent compléter et en partie corroborer mon jugement. « L’opinion prédominante sur Boole est probablement qu’il regardait la logique comme une branche des mathématiques, qu’en fait il appliquait simplement les règles mathématiques aux problèmes logiques. C’est là une méprise très-naturelle, et elle est même inévitable après une lecture superficielle. Il y a trois caractères saillants de ce système qui ont contribué à cette manière de voir. Le premier est sa doctrine d’ « expansion » ou de « développement » d’une « fonction. » Le second, qui y joue un rôle considérable, est son procédé d’ « élimination. » Le troisième et dernier n’est pas tant une méthode ou un procédé qu’un postulat général qui sert de base à tout le système. C’est le plus distinctif de tous et il différencie, croyons-nous, sa théorie de celle des autres écrivains. Il consiste dans la hardiesse, pour ne pas dire l’audace, avec laquelle il pousse ses procédés à travers des étapes (M. J. Venn songe ici à des transformations de formules) qui n’ont aucune signification, ni logique, ni autre, c’est-à-dire, qui n’admettent aucune interprétation possible, pourvu qu’ils aboutissent à un résultat interprétable. C’est une manière de faire assez fréquente en mathématique, mais cela semble une innovation tout-à-fait osée en logique. »
- ↑ The relation of Logic to Language (brochure sans aucune indication et sans nom d’imprimeur). Au mois de juin dernier je m’étais adressé à M. le professeur Robertson de Londres pour obtenir des renseignements sur les travaux des Anglais. C’est lui qui m’a fait connaître et qui m’a communiqué cet opuscule que je suis heureux de pouvoir signaler au public français.
- ↑ Drobisch a ramené ce rapport à une loi logarithmique. Ueberweg (System der Logik, 4e éd., p. 114 sqq) démontre parfaitement la fausseté de cette loi et les difficultés d’une pareille tentative.
- ↑ Sur l’emploi des cercles pour rendre les raisonnements sensibles aux yeux, voir Ueberweg, op. cit., p. 239.
- ↑ La négation n’a pas la même portée dans toutes les langues. Voir un travail sur la théorie de la négation dans la langue grecque, que j’ai inséré dans la Revue de l’instruction publique en Belgique, 1876, et où je fais voir la différence logique des deux négations que possède le grec. Voir aussi ma Logique scientifique.